all

Теория вероятностей

MIPT Осень 2012 г.

Содержание

Усиленный закон больших чисел для с.в. с конечным математическим ожиданием 43

1

2

Введение

Предмет изучения теории вероятностей: Математический анализ случайных явлений.

Эксперименты бывают:

∙Детерминированный результат (изучают другие науки)

∙Случайный результат (теория вероятностей)

Одиночные результаты случайных экспериментов не позволяют обнаружить закономерности, однако при большом числе результатов однородных случайных экспериментов обнаруживается устойчивость частот .

Пример 1. Подбрасывание монетки:

Бюфорон, XVIII век, 4040 подбрасываний, 2048 раз выпал орел, частота 0,508. . .

Пирсон, XIX век, 24000 подбрасываний, 12012 раз выпал орел, частота 0,5005. . .

Принцип устойчивости частот:

Частота осуществления какого-либо исхода в последовательности однородных случайных экспериметов сходится к некоторому числу [0, 1].

Пусть - некоторое событие, ( ) - количетсво появлений в результатах случайных экспериментов после испытаний. Тогда

( ) −−−→ ( ) – вероятность события .

→∞

Однако с математической точки зрения это неудобно. Нужно предложить другое определение вероятности, для которого будет наблюдаться устойчивость частот.

Вероятностное пространство

В основе теории вероятностей лежит понятие вероятностного пространства ( , , ) (т.н “тройки Колмогорова”)

1 — пространство элементарных событий .

— называется элементарным событием .

В результате случайного эксперимента получаем один и ровно один элемент.

2— -алгебра подмножеств на . Элементы называются событиями.

.

Определение 1. Система подмножеств множества называется алгеброй, если:

2., ∩

3.,

3

Упражнение 1. Алгебра замкнута относительно операций:

1.,

2.,

Определение 2. = , называется дополнительным событием к событию .

Пример 2.

1.* = {?, } — тривиальная алгебра

2.* = 2Ω (все подмножества ) — дискретная алгебра

{ }

3.= ?, , , — алгебра “порожденная”

4.Конечные объединения подмножеств вида [ , ), (−∞; 0), [ , +∞) образуют алгебру.

Определение 3. Система подмножеств множества называется -алгеброй, если:

Упражнение 2.

Пример 3.

1.* — тривиальная -алгебра

2.* — дискретная -алгебра

3.конечная алгебра является -алгеброй.

4.[ , ), (−∞; ), [ , +∞) — не -алгебра.

3 - вероятностная мера на ( , )

Определение 4. Пара ( , ) множества с заданной на нем -алгеброй называется измеримым пространством.

Определение 5. Отображение : → [0; 1]

называется вероятностной мерой(или вероятностью) на ( , ), если:

1.( ) = 1

2.Для последовательности { , N} , такой, что ̸= : ∩ = ? выполнено свойство счетной аддитивности:

( ∞ ) ∞

∑

= ( )

=1 =1

4

Утверждение 1.

1.(?) = 0

2.Если ∩ = ?, то ( ) = ( ) + ( ) (свойство конечной аддитивности)

3.( ) = 1 − ( )

4.( ) = ( ) + ( ) − ( ∩ )

5.1, . . . ,

( )

∑

6 ( )

=1 =1

6. Если , то ( ) 6 ( )

Доказательство.

3.= |по 2| 1 = ( ) + ( )

4.= ( ( ∩ ))

( ) = ( ) + ( ( ∩ ))

= ( ∩ ) ( ( ∩ ))

( ) = ( ∩ ) + ( ( ∩ ))

Осталось отнять вычесть одно равенство из другого.

5. Если = 2 — то это пункт 4). По индукции

6. Следует из 4).

Определение 6. Будем обозначать ↓ → +∞, если для последовательности событий { , N} выполнены свойства:

5

Доказательство.

( ) Пусть - вероятностная мера, а ↓ ?.

Доказательство.

1.Надо рассмотреть =

2.Надо рассмотреть =

Дискретные вероятностные пространства

В дискретном случае множество элементарных исходов – счетно или конечно.

Сигма-алгебру на выбирают дискретной, = * = 2Ω

Тогда вероятность можно задать как функцию на :

6

IКлассическая модель

Вклассической модели – конечно, все элементарные события равновероятны:

1

: ( ) = | |

Тогда : ( ) = | | | |

Пример 4.

1.Бросок монеты. = {Орел, Решка}.(Орел) = (Решка) = 1/2

2.Бросок кости. = {1, . . . , 6}

( ) = 1/6 = 1 . . . 6

3. Бросок двух монет. "Заблуждение Даламбера". = { , , } Кажется, что все исходы имеют верятность 1/3

Проблема в различимости монет.

Если они различимы, то = { , , , }, и вероятности событий равны 1/4

(выпал 1 орел и 1 решка) = 1/2

4.Схема испытаний Бернулли. = { = ( 1, . . . , ) | {0, 1} }. | | = 2Ω

Эта модель отвечает броскам различимых монет.

IIГеометрические вероятности

Здесь R , > 1 и для определен, конечен и положителен его объем ( ) > 0.

Сигма-алгебра состоит из тех для которых тоже определен объем ( )

Тогда вероятность задается так:

( ) =

( )

( )

Подобная модель – ествественное продолжение классической модели на случай непрерывных пространств.

Пример 5. Задача о встрече:

Два товарища договорились встретиться утром на остановке. Каждый приходит в случайное время между 9 и 10, ждет 15 минут, потом уезжает.

Какова вероятность встречи?

Решение. Пространство элементарных событий – это квадрат [9, 10] × [9, 10].

Время прихода вервого и время прихода второго — случайная точка ( , ) [9, 10] × [9, 10].

Изобразим пространство событий геометрически:

7

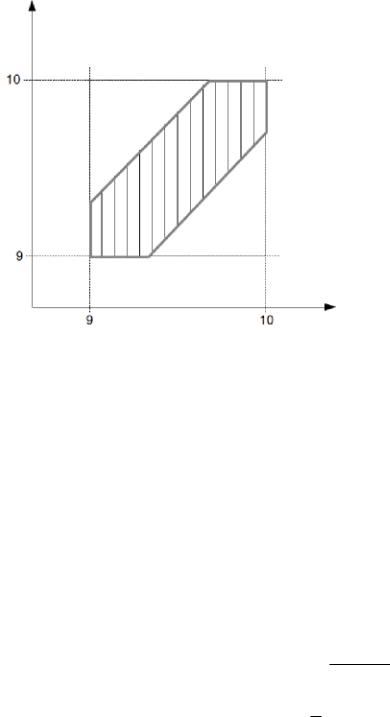
Заштрихованная область = { ( , ) | , [9; 10], | − | < 1/4 }.

Нужно найти меру этой области:

( ) = 1 − (3/4)2 = 7/16

( ) = 1

(они встретятся) = ( )/ ( ) = 7/16

Условные вероятности

Пусть ( , , ) – вероятностное пространство.

Определение 1. Для , т.ч. ( ) > 0 условной вероятностью события при условии называют

( | ) = ( ∩ )

( )

если же ( ) = 0, то ( | ) = 0,

Упражнение 3. Если ( ) > 0, то функция ( ) = ( | )

тоже является вероятностной мерой на ( , ).

Определение 2. Систему событий { }∞=1 называют разбиением множества , если:

1. ̸= : ∩ = ?

∞

2.=

=1

В этом случае также говорят, что { }∞=1 обрезует полную группу несовместных событий.

Лемма 1 (формула полной вероятности).

Пусть { }∞=1 - разбиение . Тогда для :

∞

∑

( ) = ( | ) ( )

=1

8

Доказательство. Рассмотрим событие

=1 =1

Пример 6. В ящике всего шаров, из них - белых. Последовательно, без возвращения, вынимаем по одному шару. Обозначим = {на -том шаге вынули белый шар}.

Доказать:

( ) =

Первое решение: воспользоваться симметрией. Второе решение: в лоб

Введем события ( ) = {среди первых − 1 шара вынули ровно белых} Тогда ( ) образуют разбиение, = 0 . . .

Легко видеть, что

−

( | ( )) = − + 1

( ( )) = − ( − 1) . . . ( − + 1)( − ) . . . ( − − + 1 + ) =

1 ( − 1) . . . ( − + 1)

Отсюда:

Системы множеств

Пусть - некоторое множество

Определение 1. Система подмножеств множества называется - системой, если , выполнено ∩

Определение 2. Система подмножеств множества называется - системой, если

1.

9

удовлетворяет ↑ (т.е +1 . . . и = ), то

Лемма 3 (о - и - системах). Система подмножеств является -алгебройона является -системой и -системой одновременно.

Доказательство.

( ) очевидно.

( ) Для

= т.к. − -система ( и , свойство 2)

Также имеется замкнутость относительно ∩ в ( − -система) является алгеброй Покажем, что она -алгебра:

Тогда в силу свойства 3) -системы, . Значит – -алгебра

Пример 7. = {1, 2, 3, 4}= {?; (1, 2); (1, 3); (1, 4); (2, 3); (2, 4); (3, 4); }

Тогда – это -система, но не алгебра.

Лемма 4 (о существовании минимальной системы).

Пусть – система подмножеств .

Тогда существует минимальная(по включению) алгебра (или -алгебра, -система, -система) содержащая и обозначаемая ( ) ( ( ), ( ), ( ))

Доказательство. Рассмотрим * = 2Ω – дискретная -алгебра. Она является алгеброй( -алгеброй,-системой, -системой), содержащей , т.е множество интересующих нас систем не пусто.

Рассмотрим ( ) ( ( ), ( ), ( )) – пересечение всех алгебр ( -алгебр, -систем, -систем), содержащих . Тогда ( ) ( ( ), ( ), ( )) тоже будет являться алгеброй ( -алгеброй, - системой, -системой), содержащей .

При этом она будет минимальной по включению.

Пример 8.

1.Пусть = { ( , ) | < R } – система интервалов.

Тогда минимальная -алгебра, содержащая , называется борелевской -алгеброй на прямой и обозначается (R)

(R) = ( )

2.Рассмотрим в R систему подмножеств вида

10