The BWB (see Figure 1.15) design for larger aircraft has proven merits over conventional designs but awaits technological and market readiness. Interesting deductions are made in the following sections.

3.20.1 The Square-Cube Law

For an example, increase the linear dimensions of a solid cube from 1 to 2 units. From the following example, it can be seen that the increase in weight is faster than the increase in area (the subscript 1 represents the small cube and the subscript 2 represents the larger cube):

area2 = area1 × (length2/length1)2, a 4-fold increases from 6 to 24 square units volume2 = volume1 × (length2/length1)3, an 8-fold increase from 1 to 8 cube units

Applying this concept to a wing, increasing its span (i.e., linear dimension, b – maintaining geometric similarity) would increase its volume faster than the increase in surface area, although not at the same rate as for a cube. Volume increase is associated with weight increase, which in turn would require stiffening of the structure, thereby further increasing the weight in a cyclical manner. This is known as the square-cube law in aircraft design terminology. This logic was presented a halfcentury ago by those who could not envisage very large aircraft.

Then,

wing-loading, W/Sw b

This indicates that for the given material used, because of excessive weight growth, there should be a size limit beyond which aircraft design may not be feasible. If the fuselage is considered, then it would be even worse with the additional weight.

Yet, aircraft size keeps growing – the size of the Airbus A380 would have been inconceivable to earlier designers. In fact, a bigger aircraft provides better structural efficiency, as shown in Figure 4.6, for operating empty weight fraction (OEWF) reduction with maximum takeoff weight (MTOW) gain. Researchers have found that advancing technology with newer materials – with considerably better strength- to-weight ratio, weight reduction by the miniaturization of systems, better high-lift devices to accommodate higher wing-loadings, better fuel economy, and so forth – has defied the square-cube law. Strictly speaking, there is no apparent limit for further growth (up to a point) using the current technology.

The author believes that the square-cube law needs better analysis to define it as a law. Currently, it indicates a trend and is more applicable to weight growth with an increase in aspect ratio. What happens if the aspect ratio does not change? The following section provides an excellent example of how a low aspect ratio can compete with a high aspect-ratio design.

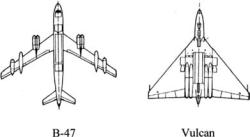
Figure 3.41. Torenbeek’s comparison between a B-47 and a Vulcan

3.20.2 Aircraft Wetted Area (AW) versus Wing Planform Area (Sw)

The previous section raised an interesting point on aircraft size, especially related to wing geometry. This section discusses another consideration on how the aircraft wing planform area and the entire aircraft wetted surface areas can be related. Again, the wing planform area, SW, serves as the reference area and does not account for other wing parameters (e.g., dihedral and twist).

The conflicting interests between aerodynamicists and stress engineers on the wing aspect ratio presents a challenge for aircraft designers engaged in conceptual design studies (this is an example of the need for concurrent engineering). Both seek to give the aircraft the highest possible lift-to-drag (L/D) ratio as a measure of efficient design. Using Equations 3.23 and 3.31, the following can be shown (i.e., incompressible flow):

drag,D = qSWCD = qSW(CDP + CDi )

or

Clearly, CDP wetted area, AW and CDi is (1/AR) = SW/b2 (from Equation 3.43).

This is an informative parameter to show how close the configuration is to the wing– body configuration. Section 4.5 provides statistical data for various designs.

Torenbeek [5] made a fine comparison to reveal the relationship between the aircraft wetted area, AW, and the wing planform area, Sw. Later, Roskam [6] presented his findings to reinforce Torenbeek’s point, whose result is shown in Figure 3.41.

Toreenbeck compared an all-wing aircraft (i.e., the Avro Vulcan bomber) to a conventional design (i.e., Boeing B47B bomber) with a similar weight of approximately 90,000 kg and a similar wing span of about 35 m. It was shown that these designs can have a similar L/D ratio despite the fact that the all-wing design has an aspect ratio less than one third of the former. This was possible because the all-wing aircraft precludes the need for a separate fuselage, which adds extra surface area and thereby generates more skin-friction drag. Lowering the skin-friction drag by having a reduced wetted area of the all-wing aircraft compensates for the increase in induced drag for having the lower aspect ratio.

All-wing aircraft provide the potential to counterbalance the low aspect ratio by having a lower wetted area. Again, the concept of BWB gains credence.

Table 3.1 provides statistical information to demonstrate that a BWB is a good design concept to satisfy both aerodynamicists and stress engineers with a good L/D ratio and a low-aspect-ratio wing, respectively. In the table, a new parameter – wetted aspect ratio, b2/AW = AR/(AW/SW) – is introduced.

The table provides the relationship among the aspect ration, wing area, and wetted area and how it affects the aircraft aerodynamic efficiency in terms of the ratio. Within the same class of wing planform shape, the trend shows that a higher aspect ratio provides a better L/D ratio. However, all-wing aircraft (e.g., BWB) provide an interesting perspective, as discussed in this section.

Figure 3.42. Additional vortex lift

3.20.3 Additional Vortex Lift

Stalling of conventional wings, such as those configured for high-subsonic civil aircraft, occurs around the angle of attack, α, anywhere from 14 to 18 deg. Difficult maneuvering demanded by military aircraft requires a much higher stall angle (i.e., 30 to 40 deg). This can be achieved by having a carefully placed additional low- aspect-ratio lifting surface – for example, having a LE strake (e.g., F16 and F18) or a canard (e.g., Eurofighter and Su37). BWB configurations also can benefit from this phenomenon.

At high angles of attack, the LE of these surfaces produces a strong vortex tube, as shown in Figure 3.42, which influences the flow phenomenon over the main wing. Vortex flow has low pressure at its core, where the velocity is high (refer to aerodynamic textbooks for more information).

The vortex flow sweeping past the main wing reenergizes the streamlines, delaying flow separation at a higher angle of attack. At airshows during the early 1990s, MIG-29s demonstrated flying at very high angles of attack (i.e., above 60 deg); their transient “cobra” movement had never before been seen by the public.

3.20.4 Additional Surfaces on Wing

Flaps and slats on a 2D aerofoil are described in Section 3.10. This section describes their installation (Figure 3.43a) on a 3D wing.

Flaps comprise about two thirds of an inboard wing at the trailing edge and are hinged on the rear spar (positioned at 60 to 66%; the remaining third by the aileron) of the wing chord, which acts as a support. Slats run nearly the full length of the LE. The deployment mechanism of these high-lift devices can be quite complex. The associated lift-characteristic variation with incidence is shown in Figure 3.43b. Slat deployment extends the wing maximum lift, whereas flap deployment offers incremental lift increase at the same incidence.