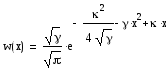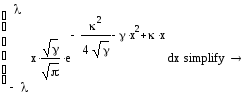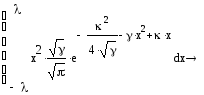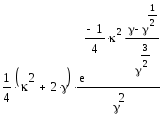1.3 Обратная задача о моментах
Какова бы ни была весовая функция, задачу о моментах всегда можно решить и тем самым получить соответствующее семейство ортогональных полиномов. Как видно из приведенных ниже вычислений, даже простейшая нормальная плотность вероятности приводит к ортогональным полиномам. Если мы применяем простую экспоненциальную функцию, то мы получаем семейство эрмитовых полиномов. Мы решаем обратную задачу – найти весовую функцию, зная полиномы. Проблема заключается в том, что данные полиномы еще не ортогональны, поэтому весовая функция должна присутствовать в обеих частях уравнения.
|
|
(1.84) |
|
|
(1.85) |
|
|
(1.86) |
Матрица Гамбургера, возникающая из задачи Гамбургера о моментах:
|
|
(1.87) |
Ниже приведено произведение определителей матриц Ганкеля:
|
|
(1.88) |
|
|
(1.89) |
|
|
(1.90) |
|
|
(1.91) |
|
|
(1.92) |
|
→
|
(1.93) |
|
|
(1.94) |
|
|
(1.95) |
Ниже приведены первые четыре полинома, полученные как собственные решения рассмотренного уравнения Штюрма-Лиувилля. Они еще не являются ортогональными, следовательно, необходима процедура ортогонализации с некоторой весовой функцией. Задача заключается в том, чтобы найти подходящую функцию плотности вероятности в качестве весовой функции, которую можно интерпретировать как собственное распределение, эквивалентное линейному пространству, определяемому полиномами.
|
|
(1.96) |
|
|
(1.97) |
|
|
(1.98) |
|
|
(1.99) |
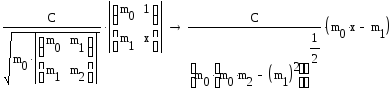
Определитель матрицы Гамбургера умножается на C, произвольную постоянную, и делится на квадратный корень из произведения двух определителей Ганкеля низшего порядка. Порядок матрицы должен совпадать с порядком полинома.
|
|
(1.100) |
Полином, основанный на матрице Гамбургера – парный к φ1(x) при ортогонализации последнего.
|
|
(1.101) |
Теперь перейдем к задаче вариационного исчисления. Определим ограничения в отношении моментов, скалярного произведения неизвестной весовой функции и необработанного полинома первого порядка, и взвешенной нормы отклонения полинома первого порядка, получившегося с помощью матрицы Гамбургера из ортогонализации полинома первого порядка φ1(x).
|
|
(1.102) |
|
|
(1.103) |
Положим N=1. После упрощения и приведения подобных получим:
|
|
(1.104) |
Полученное выражение является функционалом, подлежащим оптимизации, в котором неизвестная функция w(x) рассматривается как неизвестная переменная. Все ограничения включены в данный функционал. Теперь нам необходимо решить уравнение Эйлера-Лагранжа. По сути дела, мы вновь обращаемся к уравнению Штюрма-Лиувилля.
|
|
(1.105) |
|
|
(1.106) |
|
→
|
(1.107) |
Мы рассматриваем весовую функцию w(x) как первую производную функции меры. Следовательно, δ – это вторая производная функции меры:
|
(x) = w'(x) = m''(x) |
(1.108) |
Таким образом, уравнение Эйлера-Лагранжа не содержит саму неизвестную функцию меры и представляет собой дифференциальное уравнение первого порядка по отношению к первой производной функции меры. Если бы мы были заинтересованы в поиске самой функции меры, то уравнение представляло бы собой уравнение Штюрма-Лиувилля второго порядка.
Приравняем (1.108) к нулю и домножим обе части на –w, получив таким образом более удобную спецификацию:
|
|
(1.109) |
Введем замены переменных:
|
|
(1.110) |
|
|
(1.111) |
|
|
(1.112) |
|
|
(1.113) |
|
|
(1.114) |
|
|
(1.115) |
Перегруппируем относительно x степень экспоненты, получим:
|
|
(1.116) |
В итоге получим следующую весовую функцию:
|
|
(1.117) |
Однако (1.117) еще не является конечным результатом, поскольку содержит в себе множители Лагранжа, которые должны быть исключены, чтобы гарантировать выполнение всех ограничений. Поскольку λ исчезла, мы будем использовать данное обозначение для обозначения пределов интегрирования ниже:
|
|
(1.118) |
Упростим и решим относительно K.
|
|
(1.119) |
Это ограничение, которому должно удовлетворять K, чтобы выполнялось условие:
|
|
(1.120) |
|
|
(1.121) |
Это выражение (1.121) должно быть отрицательным, поэтому удобно принять γ=-θ.
|
|
(1.122) |
При выполнении первого общего ограничения мы получаем следующую весовую функцию:
|
|
(1.123) |
Все прочие ограничения учитываются последовательно сходным образом. Все интегралы находятся при бесконечной нижней границе интегрирования, что существенно упрощает вычисления.
Это момент первого порядка, который оценивается приравниванием (1.124) к ν и решением полученного уравнения относительно φ.
|
|
(1.124) |
(1.125) – момент второго порядка. Он оценивается приравниванием (1.125) к ζ и решением уравнением относительно φ.
|
|
(1.125) |
Введем замены переменных:
|
|
(1.126) |
|
|
(1.127) |
|
|
(1.128) |
Тогда
|
|
(1.129) |
Квадрат взвешенного отклонения оценивается приравниванием (1.129) к 0 и решением полученного уравнения относительно ψ.
Наконец, ниже приведено скалярное произведение, которое является матожиданием необработанного полинома первого порядка, поскольку полином нулевого порядка является просто константой N, которую мы положили равной 1.
|
|
(1.130) |
Скалярное произведение оценивается приравниванием (1.130) к υ и решением уравнения относительно η.
Таким образом, для каждой спецификации уравнения Штюрма-Лиувилля мы построили прямую систему полиномов и сопряженную систему полиномов как собственных функций сопряженного дифференциального оператора, парного к основному уравнению. Полученные полиномы задают счетное множество пространств, и в пункте 1.3 был показан способ построения функции плотности вероятности, имманентной каждому такому пространству.
Разработанный подход позволяет при минимальной исходной предпосылке (о функции мгновенной диффузии σ(x)) позволяет получить набор функций плотности вероятности, свойственных выбранному финансовому рынку, причем в процессе решения поставленной задачи мы получили эндогенно формальное описание известных поведенческих эффектов, как например эффекта изменения средних по знаку.
В рамках предложенного подхода конкретному финансовому рынку соответствует набор распределений, переключения между которыми происходят скачкообразно, что эвристически соответствует резким переменам настроения не только на валютном, но и на других финансовых рынках.




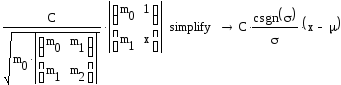
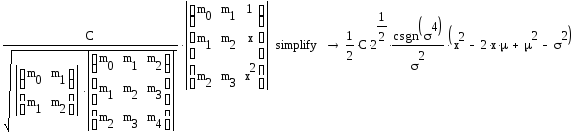
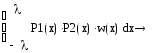
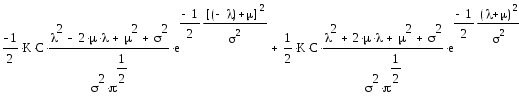
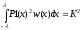
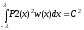

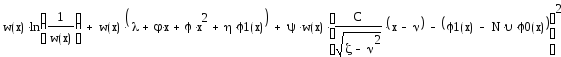
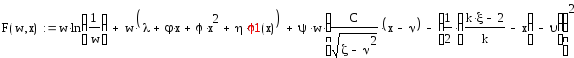
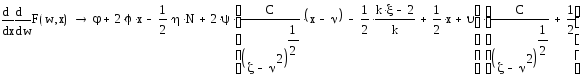
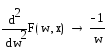
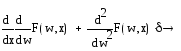
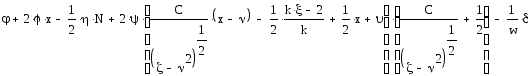

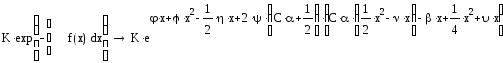

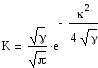
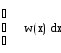 = 1
= 1