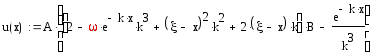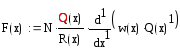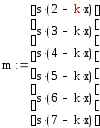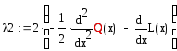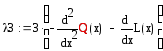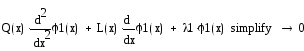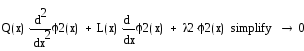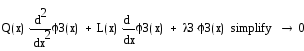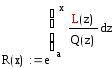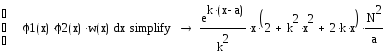1.2 Решение однородного уравнения

Затем строится система полиномов как собственных функций каждого такого оператора. Систем полиномов оказывается, таким образом, столько же, сколько исходных видов мгновенной диффузии мы пробуем. Заметим, что весь сценарий может начинаться также и заданием функций мгновенного сдвига, тогда приходится решать промежуточное дифференциальное уравнение второго порядка, а значит, итоговое количество пространств удваивается.

Выбор исходного предположения зависит от экспертной позиции – часть финансовых аналитиков, к которой принадлежит и автор данного доклада, предполагает, что интуитивное восприятие trader’ом рыночной обстановки – это прежде всего интуитивная картина неопределённости, поэтому стартовать следует с функции мгновенной диффузии. Преобладающая часть аналитиков и практиков валютного рынка полагают, однако, что первичная интуитивная картина рынка – это прежде всего (не осознаваемая trader’ом) картина ожидаемого роста или спада, а следовательно, конструирование должно начинаться заданием функции мгновенного сдвига.

Параметру k может быть присвоено значение -1 без изменения полиномов.

(1.15)

(1.16)

(1.17)

(1.18)

(1.19)

(1.20)

(1.21)

(1.22)

(1.23)

(1.24)

(1.25)

(1.26)

(1.27)

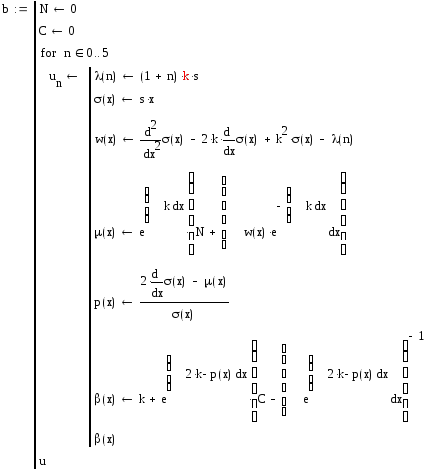
Ниже приведен алгоритм поиска собственных решений (1.28 – 1.33). Его особенностью является то, что λ влияет на получаемый эндогенно мгновенный снос, а следовательно, собственное решение является уникальным. Поэтому построить ортогональные базисные функции не представляется возможным, и мы перейдем к полиномиальным решениям.

В последовательности действий (1.28) описывается получение собственных решений оператора Штюрма-Лиувилля. Переменной F присваиваются полученные решения в зависимости от значения λ. В нашем случае мы имеем набор λ₀... λ₅, поэтому F содержит в себе пять элементов (1.31).

Решение строится на основе разложения оператора второго порядка на произведение двух операторов первого порядка, в ходе которого вводится новая функция β(x), получаемая на основе параметризующих функций уравнения Штюрма-Лиувилля. Функции β(x) в зависимости от λ_n обозначены как переменная b и получаются в результате последовательности действий (1.29) и приведены в (1.32). Функции мгновенного сноса μ(x) обозначены переменной m (1.30) и приведены в (1.33)

(1.28)

(1.29)

(1.30)

После упрощения F представляет собой следующий вектор

(1.31)

После упрощения b(x) представляет собой следующий вектор

(1.32)

После упрощения m представляет собой следующий вектор

(1.33)

Ниже приведены полиномы φ3(x), φ2(x) и φ1(x) (формулы 1.34-1.36) и соответствующие собственные значения (1.37)-(1.39). Эти полиномы являются собственными решениями уравнения Штюрма-Лиувилля при заданной функции мгновенной диффузии σ(x).

(1.34)

(1.35)

(1.36)

(1.37)

(1.38)

(1.39)

(1.40)

(1.41)

(1.42)

(1.43)

(1.44)

(1.45)

Убедимся, что мы действительно нашли собственные функции:

(1.46)

(1.47)

(1.48)

Тогда соответствующий вронскиан будет выглядеть так (1.49):

(1.49)

Существенным условиям получения полиномов является использование параметризующих функций из сценария решения уравнения Штюрма-Лиувилля. Функция мгновенного сноса μ(x) получается эндогенно, исходя из заданной функции мгновенной диффузии σ(x).

(1.50

(1.51)

Функции P0(x), P1(x), P2(x) задаются выражениями (1.17), (1.18), (1.20). При выбранной σ(x)

(1.52)

Функции Q(x) и L(x) задаются выражениями (1.22), (1.23).

(1.53)

(1.54)

(1.55)

(1.56)

(1.57)

(1.58)

(1.59)

(1.60)

Выбрав в (1.60) пределы интегрирования от а до 1, получим (1.61):

(1.61)

Теперь заменим в (1.60) φ1(x) на φ3(x) и вновь возьмем определенный интеграл с пределами от а до 1, результат приведен в (1.62).

+ +

(1.62)

В данном случае мы получаем λ1=-1, λ2=-2, λ3=-3. Определитель матрицы Вронского для φ1(x), φ2(x) и φ3(x) (1.63) свидетельствует о независимости полиномов.

(1.63)

Выбрав σ(x) = s²x², мы получим μ(x) = s²x(2 - kx) и семейство полиномов (1.64)-(1.66).

(1.64)

(1.65)

(1.66)

Выбрав σ(x) = sx, мы получим μ(x) = s(1 - kx) и семейство полиномов (1.67)-(1.69).

(1.67)

(1.68)

(1.69)

Рассмотрим случай, когда мгновенная диффузия имеет особую точку x=ξ и задается так (1.70):

(1.70)

В этом случае мы получим мгновенный снос (1.71):

(1.71)

Функции P0(x), P1(x), P2(x) по-прежнему задаются выражениями (1.17), (1.18), (1.20).

(1.72)

(1.73)

(1.74)

(1.75)

(1.76)

(1.77)

(1.78)

(1.79)

(1.80)

(1.81)

Обозначим 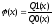. Как видно из (1.77), Q2(x) обнуляется, поэтому в уравнении остаются вторая и первая производные, однако исчезает неизвестная функция. Следовательно, необходимо решить уравнение относительно первой производной как неизвестной функции, а затем проинтегрировать решение, чтобы получить u(x). Иными словами, из решения дифференциального уравнения первого порядка мы получаем промежуточное решение, первообразная которого будет решением дифференциального уравнения второго порядка.

(1.82)

(1.83)

Итак, построив систему полиномов для каждой спецификации уравнения Штюрма – Лиувилля, мы строим также сопряженную систему полиномов как собственных функций сопряженного дифференциального оператора, парного к основному уравнению. Затем каждую такую систему подвергаем ортонормировке по Граму на избранном ограниченном отрезке числовой оси. Значения доходности, которые, в принципе, определены на всей действительной шкале, отображаются на ограниченный отрезок любым подходящим преобразованием, при этом их эмпирическая функция плотности вероятности преобразовывается с помощью оператора Перрона – Фробениуса (такая функция в общем случае не нужна, поскольку задача исследования – в построении распределений, эндогенных для конструируемых пространств).

Полученные пространства, задаваемые счетным бесконечным множеством ортонормированных базисных полиномов, позволяют построить имманентную каждому такому пространству функцию плотности вероятности – это делается в терминах задачи о моментах. При заданном наборе ортогональных полиномов, на которые натянуто подпространство, достаточное, к примеру, для разложения априорных функций плотности с относительным уклонением, не превышающим некоторого допустимого уровня, первые четыре начальных момента выражаются через эти полиномы. После этого выстраивается система обобщенных функций («распределений», по Л.Шварцу) и решается, начиная с первого момента, в отношении искомой функции. Решение базируется на перестановочности основной и искомой функции в операторе взятия производной от обобщенной функции. Эндогенное распределение для данного пространства построено. После этого мы переходим к решению второй задачи из двух, поставленных выше.

Предполагается существование интегрального оператора, соответствующего каждому дифференциальному оператору, собственными решениями которых служат полученные полиномы. Поскольку ортонормировка осуществляется с единичным весом, собственные функции дифференциального оператора выступают также собственными функциями оператора интегрального. Воздействие оператора на каждый полином заключается в умножении этого полинома на соответствующее собственное значение, определяемое по способу лорда Рэйли. В ограниченном подпространстве интегральный оператор предполагается матрично представимым – это позволяет перейти от непрерывного представления к дискретному представлению функций в виде векторов из весов их разложения по базисным полиномам.

Представляем пространство как прямое произведение двух подпространств, при этом матричное представление интегрального оператора предстаёт как произведение двух матричных операторов, один из которых имеет Эрмитову форму. Система его собственных векторов есть унитарный оператор, сохраняющий норму преобразовываемого им вектора. Поскольку этот вектор – это вектор весов разложения функции плотности вероятности эндогенного распределения, то, по теореме Парсеваля, оператор, сохраняющий норму вектора, обеспечивает пошаговую эволюцию распределения с сохранением нормы функции. Подчеркнем, что мы отказываемся в этом подходе от непрерывной зависимости от физического времени, что отвечает выявленному в поведенческих финансах (Либерман) эффекту переживания будущих горизонтов планирования как здесь и теперь достигнутых, без субъективного психологического проживания точка за точкой всего физического времени между горизонтами инвестирования.

В предыдущих исследованиях большое внимание уделено, в частности, численному моделированию ряда психологических эффектов, поскольку поведение финансовых рынков, по крайней мере в краткосрочном аспекте, есть, по моему глубокому убеждению, всецело «человеческий» феномен. И вопрос об унитарных операторах занимает в этом подходе особое место.

Нами неоднократно проводились численные исследования, показавшие, что максимизация «неожиданности», т.е. новой информации, измеримой в терминах относительной энтропии, при сохранении нормы функций плотности вероятности – это формализм, высоко результативный в прогнозировании различных типов финансовых рынков, поскольку он позволяет единым «пакетом» получить как эмпирически наблюдаемую картину систематических подвижек центров распределения (mean reverting) и изменений дисперсии без добавления новой информации при удалении горизонта предвидения, т.е. картину, совместимую с эмпирикой финансовых прогнозов, так и учесть иные, более сложные поведенческие эффекты – в частности, систематическое чередование чрезмерной и недостаточной уверенности в собственных прогнозах, многократно подтвержденное психологическими исследованиями (см., напр., Koriat и др.).

Полагаю, что органичное объединение поведенческих результатов с формализмом в терминах математического анализа составляет важную научную новизну в финансовой теории.