II. Задача «Уклонение от налогов»

Будет ли уклоняться от уплаты налогов предприятие, имеющее функцию полезности , если его доходW составляет 100 млн. долларов, подоходный налог – 20%, штраф при обнаружении уклонения – 60%, вероятность проверки налоговой инспекции – 0,3?

Решение

Обозначим через Х объем дохода, декларируемый предприятием для уплаты подоходного налога, интервал возможных значений Х в условиях задачи определяется тем, что предприятие может уклоняться от уплаты налогов и не декларировать ничего: Х = 0, или декларировать полную сумму дохода: Х = 100.

Если предприятие декларирует сумму дохода Х, то оно заплатит налог с этой суммы 0,2X, его доход составит 100 – 0,2X, а полезность будет определяться как при отсутствии проверки налоговой инспекции. Если же проверка состоится, то помимо налога предприятие заплатит еще и штраф с утаенной от налогообложения суммы, размером 0,6(100–X), оставшийся после проверки доход предприятия 100–0,2X–0,6(100–X) = 40 + 0,4Х позволит ему иметь полезность, равную .

Выпишем функцию ожидаемой полезности предприятия как математическое ожидание полезности дохода, которую будет иметь предприятие в случае проверки налоговой инспекции и при ее отсутствии:

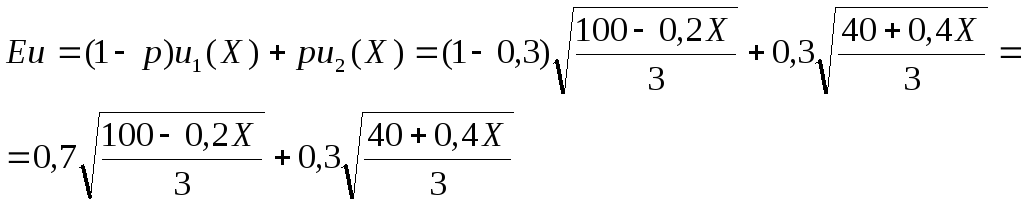
Исследуем полученную функцию на экстремум. Необходимое условие экстремума функции:

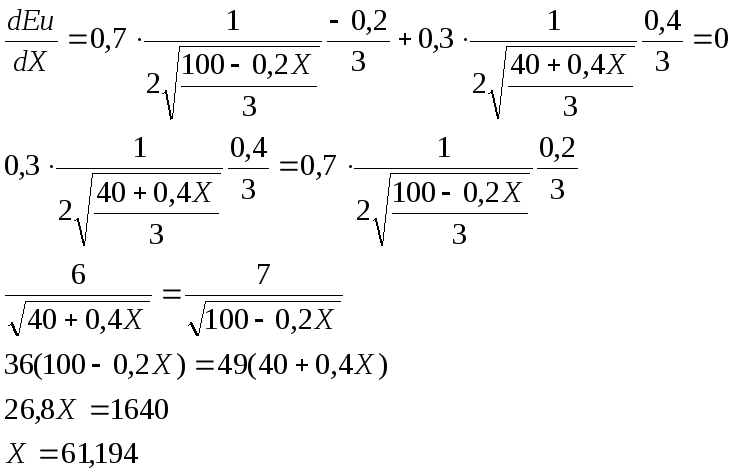
X = 61,19 – критическая точка, подозрительная на экстремум.

Проверим выполнение первого достаточного условия, для этого определим знак dEU/dX при Х = 0:

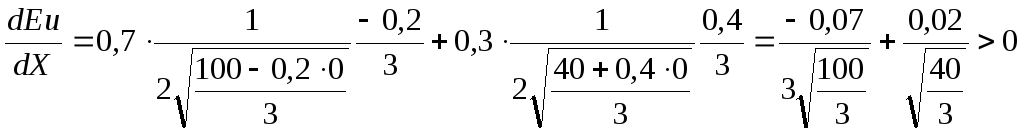
Так как при dEU/dX(Х = 0) > 0 и других точек экстремума внутри интервала (0;100) не может быть, то при изменении Х от 0 до 100 функция ожидаемой полезности растет и принимает наибольшее значение при Х = 61,19. Следовательно, максимизируя полезность, предприятие в условиях задачи будет декларировать только 61,19 млн.долл. своего дохода.

Вывод: предприятие будет уклоняться от налогов, так как вероятность контроля невысока, хотя уровень штрафных санкций и высок. Предприятию, получающему доход в 100 млн. долларов, выгодно декларировать только 61,19 млн.долл. дохода.

III. Задача «Трагедия общин»

Деревня находится на побережье, где можно добывать устриц. Разрешение на ловлю дает местная мэрия. Известно, что общий доход от ловли, приходящийся на х лодок в месяц, зависит от количества лодок: TR(х)=100х–2х² (тыс. долларов), где х – количество лодок. Эксплуатация одной лодки обходится в 8 тыс. долларов в месяц.

Определите:

1) АR, МR, МС и их графики;

2) Как много лодок будет использоваться для ловли, если мэрия не имеет возможности контролировать наличие разрешений у ловцов, а последние не утруждают себя их получением и индивидуально принимают решения о ловле? Какова будет прибыль каждой лодки?

3) Сколько лодок будет использоваться, если мэрия по-прежнему не имеет возможности контролировать наличие разрешений у ловцов, но последние объединились в артель и максимизируют прибыль? Какова будет прибыль артели и прибыль каждой лодки?

4) Отобразить полученные результаты на графике.

5) Что должна сделать мэрия, чтобы ограничить число лодок и максимизировать прибыль (косвенными методами)?

6) Сформулировать выводы по задаче в терминах институционального подхода.