
Diskretna_Ispit_Avtosokhranenny__Avtosokhranen
.Pdf1.Інтуїтивне поняття множини. Основні принципи теорії множини.
Поняття множини – одне з основних, якщо не основне, поняття математики. Воно немає точного визначення, і його слід віднести до аксіоматичних понять. Такими аксіоматичними поняттями, наприклад, в елементарній геометрії є поняття точка, пряма, площина.
ножин — одне з основних понять сучасної математики. Строго воно не визначається, але може бути дано інтуїтивне визначення множини як сукупності певних і різних об'єктів довільної природи, яка розглядається як одне ціле. Об'єкти, які складають множину, називаються її елементами. Наприклад, можна говорити про множину усіх книг в певній бібліотеці, множину літер українського алфавіту або про множину всіх коренів певного рівняння тощо.
Часто приймається формулювання інтуїтивного поняття множини Георга Кантора, основоположника цієї теорії: «Довільне зібрання певних предметів нашої інтуїції чи інтелекту, які можна відрізнити один від одного і які уявляються як єдине ціле, називається множиною. Предмети, які входять до складу множини, називаються її елементами».
Суттєвим пунктом канторівського розуміння множини є те, що зібрання предметів розглядається як один предмет («уявляється як єдине ціле»). Основна увага тут переноситься з окремих предметів на зібрання предметів, що, в свою чергу, можна розглядати як предмети.
Основні принципи інтуїтивної теорії множин:(по Кантору).
Інтуїтивний принцип об’ємності: дві множини рівні в тому і тільки в тому випадку, коли вони складаються з одних і тих же елементів.
X=Y, X¹Y
На основі цього принципу доведення рівності двох множин А і В зводиться до доведення, що якщо хÎА, то хÎВ і що якщо хÎВ то хÎА.
2.Опер ції н д множин ми.
Об’єдн ння А і В (А В) – множина, що складається з усіх елементів множин А, всіх елементів множини В і не містить ніяких інших елементів (рис 1.1,а), тобто А В = {x | x A або x В}.
Переріз (перетин) А і В (А∩В) – множина, що складається з тих і тільки тих елементів, які належать одночасно множині А та множині В, тобто А∩В
= {x | x A та x В}.
Різниця А і В або відносне доповнення В до А (А–В, A\B) – множина,
що складається з тих і тільки тих елементів, які належать множині А та не належать множині В, тобто А\В = {x | x A та x В}.
Симетричн різниця (диз’юнктивн сум ) А і В (А÷В, A B) –
1
множина, що складається з усіх елементів А, які не належать множині В, й усіх елементів В, які не належать множині А (рис 1.1,г), тобто А÷В = {x |
(x A та x В} або (x A та x В)).
Абсолютне доповнення бо просто доповнення А (А’, A ) – множина, що містить усі елементи універсуму, за винятком елементів А (рис 1.1,д), тобто А’ = {x | x A).
3.З кони для опер цій н д множин ми.
Для будь-яких множин A, B, та C, виконуються такі співвідношення: комутативність:
A B = B A
A ∩B = B ∩A
асоціативність:
|
(A B) C = A (B C) |
|
(A ∩B) ∩C = A ∩(B ∩C) |
дистрибутивність операції перетину відносно об'єднання:
A (B ∩C) = (A B) ∩(A C)
A ∩(B C) = (A ∩B) (A ∩C)
Як можна спостерігати з наведених співвідношень, з точки зору основних властивостей можна провести певну аналогію між операцією об'єднання множин та операцією множення чисел, операцією перетину множин та операцією додавання чисел. Ця аналогія розвивається в наступному твердженні:
Для будь-якої підмножини A універсальної множини U, справедливі наступні співвідношення:
властивості нуля
A Ø = A
A ∩CA = Ø
властивості одиниці
A ∩U = A
A СA = U
Тут елементи Ø та U є нейтральними елементами відносно операцій та ∩ відповідно, тобто такими, що не впливають на результат операції, аналогічно
2
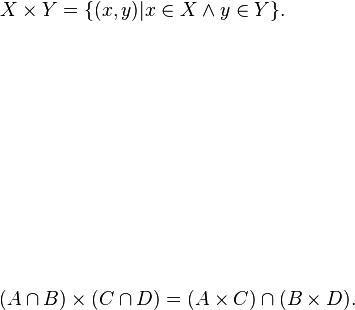
тому, як в звичайній алгебрі дійсних чисел такими елементами на операціях множення та складання є 1 та 0 відповідно. Але, на відміну від звичайного множення та складання, в алгебрі операцій перетину та об'єднання множин не існує зворотного елементу.
Для будь-яких підмножин A та B універсальної множини U, справедливі наступні твердження:
ідемпотентність
A A = A
A ∩A = A
домінування:
A U = U
A ∩Ø = Ø
поглинання:
|
A (A ∩B) |
= |
A |
|
|
A ∩(A B) |
= |
A |
|
4.Дек ртовий добуток множин. Вл стивості. |
|
|||
В теорії множин, дек ртів добуток ( |
) двох множин X та Y — |
|||
це множина усіх можливих впорядкованих пар, у яких перша компонента належить множині X, а друга — множині Y. Це поняття названо на честь відомого французького математика Рене Декарта.
Декартів добуток двох множин X та Y позначають як X×Y:
Наприклад, якщо множина X складається з 13 елементів { A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2 }, а множина Y — з 4 елементів {червоний, чорний, блакитний, зелений}, то декартів добуток цих множин є 52-елементною множиною (оскільки 13×4=52) {(A, червоний), (K, червоний), ... , (2, червоний), (A, чорний), ... , (3, зелений), (2, зелений)}.
Вл стивості:
Операція декартового добутку не є асоціативною та комутативною, тобто
(A×B)×C≠A×(B×C), A×B≠B×A.
Справедливі така тотожність відносно операції перетину (для об'єднання не вірно):
Дистрибутивність буде виконуватись для наступних операцій:
3

Для підмножин будуть вірні твердження:
Якщо  , то
, то 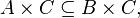
Якщо 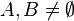 , то
, то 
5.Відношення: ун рні, бін рні, терн рні, n- рні відношення. Прикл ди.
Означення 2.3. Довільна підмножина множини А1×А2×...×Аn називається відношенням, заданим або визначеним на множинах А1, А2 ,..., Аn. Якщо А1 = А2 = ... = Аn = А, тобто річ йде про декартовий добуток n-ого ступеню множини А, то відношення R, яке задано на множинах А1 = А2 = ... = Аn, називається n-арним відношенням на множині А.
Коли (а1, а2, ..., аn) R, то говорять, що елементи ai (i = 1,..,n) знаходяться між собою у відношенні R або відношення R істинне для а1, а2, ..., аn. Якщо (а1, а2, ..., аn) R, то вважають, що R хибне для а1, а2, ..., аn. При n=1 відношення називається унарним, при n=2 – бінарним, при n=3 – тернарним.
Загалом відношення означає який-небудь зв’язок між предметами або поняттями.
Приклади бінарних відношень: відношення належності, включення множин, рівності дійсних чисел, нерівності, бути братом, ділитися на яке-небудь натуральне число, входити до складу якого-небудь колективу.
Частіше за все бінарні відношення записуються у вигляді співвідношень aRb, де R – відношення, яке встановлює зв’язок між елементами a A та b B. Наведемо ще декілька прикладів бінарних відношень.
1.Якщо А – множина дійсних чисел, то {(x,y) | x A, y A, x^2+y^2=4} є бінарне відношення на А.
2.Нехай А – множина товарів в магазині, а В – множина дійсних чисел. Тоді {(x,y) | x A, y B, y – ціна x} – відношення на множинах А та В.
3.Якщо А – множина людей, то {(x,y) | x A, y A, y є рідним x} є бінарне відношення на А.
6.Способи з д ння бін рних відношень.
Матриця та граф відношень, матриця та граф оберненого відношення, композиції відношень.
4
1.За допомогою списку(переліку), елементами якого є пари, для яких це
відношення виконується.
Приклад 3. На множинах чисел А={1,2,3,4,5,6,7,8,9}, B={24,25,26}
побудуємо відношення „дільник”, яке складається з упорядкованих пар виду (х,у), де х –дільник у , х А, у
А, у В.
В.
То R={(1,24),(1,25),(1,26),(2,24),(2,26),(3,24),(4,24),(5,25),(6,24),(8,24)}.
2. Матриці w=w(R), рядки якої відповідають елементам множини А, стовпці – елементам множини В.
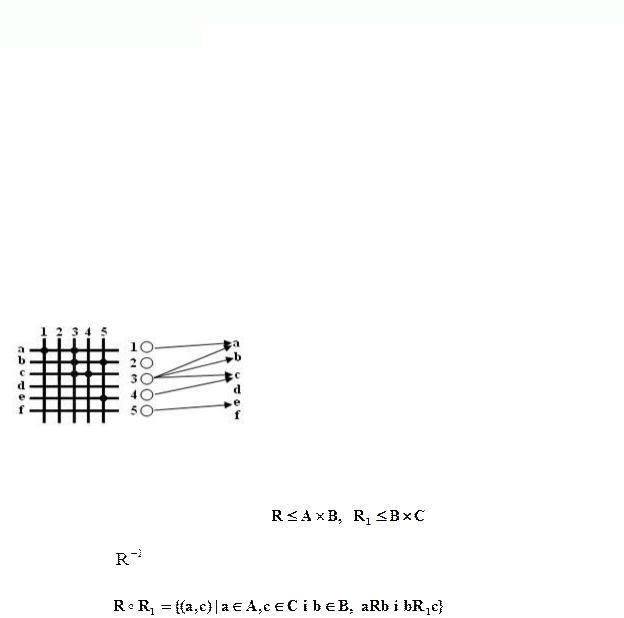
3. Бінарне відношення R має бути задано графічно: — у вигляді графіків (мал.1) і стрілкове (графом)(мал.3).
До прикладу 2.
(мал. 1) ( мал. 2 ) |
|
|
|
|
Означення: |
|
|
|
|
Нехай дано бінарні відношення |
|
. |
|
|
Відношення |
={(b,a)| aRb}, |
задане на множині В×А називають |
||
оберненим |
до |
відношень |
R, |
а |
відношення |
|
|
задане |
множині |
А×С – композицією (суперпозицією).
Нехай R і  – відношення, такі що
– відношення, такі що 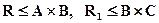 , де А,В,С – множини.
, де А,В,С – множини.
Композицією відношеньR і  називається відношення, що складається з упорядкованих пар(а,с), а
називається відношення, що складається з упорядкованих пар(а,с), а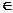 А, с
А, с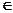 С, для яких існує елемент b
С, для яких існує елемент b B, такий, що
B, такий, що
виконуються умови (a,b)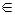 R, (b,c)
R, (b,c)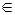
 . Композиція позначається
. Композиція позначається 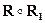 .
.
Приклад 4. Нехай R={(1,a),(3,a),(3,b),(3,c),(4,c),(5,b),(5,e)}
 ={(a,1),(a,3),(b,3),(c,3),(c,4),(b,5),(e,5)}
={(a,1),(a,3),(b,3),(c,3),(c,4),(b,5),(e,5)}
5
Тоді, згідно з означенням відношення  , потрібно взяти пару (a,b) з відношення R і знайти пару (b,c), яка є елементом відношення
, потрібно взяти пару (a,b) з відношення R і знайти пару (b,c), яка є елементом відношення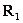 . Потім створити пару (a,c) і включити її до елементів відношення
. Потім створити пару (a,c) і включити її до елементів відношення  v.
v.
 ={(a,2),(b,4),(e,6)}
={(a,2),(b,4),(e,6)}
 = {(2,a),(4,b),(6,e)}
= {(2,a),(4,b),(6,e)}  ={(1,2),(3,4),(5,4),(5,6)}.
={(1,2),(3,4),(5,4),(5,6)}.
7.Повне, тотожне, порожнє відношення. Обл сть визн чення т обл сть зн чень відношення.
Область визначення відношення R на A та В є множина всіх а А
таких, що для деяких b B маємо (a, b) R. Іншими словами, область визначення R є множина
всіх перших координат впорядкованих пар із R. Множина значень відношення R на А та В є
множина всіх b B таких, що (a, b) R для деяких a A. Іншими словами, множина значень R є
множина всіх других координат впорядкованих пар із R.
В наведених прикладах вище, у (1) область визначення і множина значень співпадають
із множиною {t: t [-2;2]}. В (2) область визначення є множина А, а множина значень є множина всіх дійсних чисел, кожне з яких співпадає із ціною деякого товару в магазині. В (3)
область визначення і множина є множиною всіх людей, які мають рідних. Цікавими є такі окремі випадки відношень на А.
1.Повне (універсальне) відношення U = А×А, яке справджується для будьякої пари
(а1, а2) елементів з А. Наприклад, U – відношення “вчитися в одній групі” у множині А, де А – множина студентів групи ІС-21.
2.Тотожне (діагональне) відношення І, що виконується тільки між елементом і ним самим. Наприклад, рівність на множині дійсних чисел.
3.Порожнє відношення, яке не задовольняє жодна пара елементів з А. Наприклад, R –
відношення “бути братом” у множині А, де А – множина жінок.
6

8.Опер ції н д відношеннями.
Оскільки відношення, задані на А та В – підмножини А×В, то для них визначені операції об’єднання, перерізу, різниці і доповнення (наступне справедливо
для загального |
|
|
|
випадку відношення): |
|
||
|
(а, b) R1 |
(а, b) |
або (а, b) |
|
(а, b) R1∩ |
(а, b) |
і (а, b) |
|
(а, b) R1\ |
(а, b) |
або (а, b) |
|
(а, b) R’ (а, b) R (заперечення) |
||
Крім |
того, виділяються специфічні для відношень операції: обернення |
||
(симетризація) і композиція.
9.Вл стивості відношень : рефлексивене, іррефлексивне. Їх м триця т гр ф. Рефлексивне з мик ння відношення.
Означення 2.9. Нехай R – бінарне відношення у множині A (R A×A). Тоді відношення R є:
рефлексивним, якщо I R, тобто, іншими словами, воно завжди виконується між елементом і ним самим ( a A, aRa). Як приклад такого відношення можна навести відношення нестрогої нерівності на множині натуральних або дійсних чисел. Матриця рефлексивного відношення характеризується тим, що всі елементи її головної діагоналі – одиниці. Граф рефлексивного відношення – тим, що петлі є у всіх вершинах.
нтирефлексивним (іррефлексивним), якщо R∩I = , тобто якщо співвідношення aiRaj виконується, то ai ≠ aj . Це, наприклад, відношення строгої нерівності на множинах натуральних або дійсних чисел, відношення “бути старшим” у множині людей.
Матриця антирефлексивного відношення характеризується тим, що всі елементи її головної діагоналі – нулі. Граф антирефлексивного відношення не має жодної петлі.
Рефлексивним з мик нням бінарного відношення R, заданого на множині А (позначається Rr), називається відношення Rr=iAÈR.
7
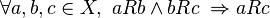
10. Вл стивості: симетричне, нтисиметричне, симетричне. Їх м триця т гр ф. Симетричне з мик ння відношень.
Означення 2.9. Нехай R – бінарне відношення у множині A (R A×A). Тоді відношення R є:
симетричним, якщо R = R -1, тобто при виконанні співвідношення aiRaj виконується співвідношення ajRai . Як приклад такого відношення можна навести відстань між двома точками на площині, відношення “бути рідним” на множині людей. Симетричність відношення спричиняє також симетричність матриці. Також для такого відношення вершини графа можуть бути пов’язані тільки парами протилежно спрямованих дуг (тобто ребрами).
симетричним, якщо R∩R -1 = , тобто із двох співвідношень aiRaj та ajRai щонайменше одне не виконується. Як приклад такого відношення можна навести відношення “бути батьком” у множині людей, відношення строгого включення в множині всіх підмножин деякого універсуму. Очевидно, якщо відношення асиметричне, то воно й антирефлексивне.
Матриця асиметричного відношення характеризується тим, що всі елементи її головної діагоналі – нулі й немає жодної пари одиниць на місцях, симетричних відносно головної діагоналі. У графа такого відношення петлі відсутні, а вершини можуть бути пов’язані тільки однією спрямованою дугою.
нтисиметричним, якщо R∩R-1 I, тобто обидва співвідношення aiRaj та ajRai одночасно виконуються тоді й тільки тоді, коли aj = ai . Як приклад можна навести нестрогу нерівність. Матриця антисиметричного відношення має ті самі властивості, що й асиметричного, за винятком вимоги рівності нулю елементів головної діагоналі. У графі такого відношення можуть бути петлі, але зв’язок між вершинами, якщо він є, також відбувається тільки однією спрямованою дугою.
11.Вл стивості відношень: тр нзитивність. |
триця т |
гр ф |
тр нзитивного відношення. Тр нзитивне з мик ння відношення. |
|
|
В математиці, бінарне відношення R на множині X є тр нзитивним, якщо для будь-яких a, b, та c з X, виконується: колиa відноситься
до b і b відноситься до c, то a відноситься до c. Формально:
8
Тр нзитивне з мик ння бінарного відношення 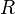 на множині
на множині  — це найменше транзитивне відношення на множині
— це найменше транзитивне відношення на множині 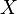 , щовключає
, щовключає 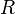 .
.
«Найменше транзитивне відношення» визначається за допомогою відношення включення.
Це можливо, позаяк відношення само є множиною (а саме підмножиною декартового квадрата множини  ). тому, якщо R1 R2, тоді R1 вважатимемо меншим за R2.
). тому, якщо R1 R2, тоді R1 вважатимемо меншим за R2.
12.Функціон льне відношення. Обр з т прообр з. Обл сть визн чення т обл сть зн чення.
Означення 3.1 Відношення f А×В називається функціон льним (або просто функцією), якщо виконується наступне:
a (a, b) f та (a, c) f b = c.
Іншими словами, кожному a A: (a, b) f відповідає один і тільки один елемент b B.
Іноді функціон льне відношення f також позначають у префіксному записі: b = f(a), де a A, b B.
Обл сть (множин ) визн чення функції буде наступна множина:
Dom f == {a A | b B, b = f(a)}.
Обл сть (множин ) зн чень функції буде наступна множина:
Im f == {b B | a A, b = f(a)}.
Очевидно, для функціонального відношення f кожний переріз за будь-яким a A містить не більше як один елемент. Якщо a Dom f , то переріз за a – порожній.
Якщо Dom f = A, то функціональне відношення f називається всюди визначеним.
Матриця функціонального відношення містить у кожному рядку не більше як один одиничний елемент, а його граф характеризується тим, що з кожної вершини може виходити тільки одна дуга (враховуючи й петлі).
Наприклад, розглянемо множини A = {1, 2, 3, 4} та B = {1, 4, 9, 16, 25}, тоді відношення R = {(1,1), (2,4), (3,9), (4,16)} та Q = {(1,1), (2,4), (3,4), (4,16)} є
функціональними.
Відношення P = {(1,1), (1,4), (3,9)}, навпаки, не є функціональним. Розглянемо інший приклад – українсько-англійський словник. Він установлює відповідність між множиною українських та англійських слів. Ця
відповідність не є функціональною (оскільки одному українському слову, як правило, ставляться у відповідність
9
декілька англійських слів); крім того, вона практично ніколи не є повністю визначеною:
завжди можна знайти українське слово, що не міститься в цьому словнику. Усяке функціональне відношення можна розглядати як функцію. При цьому перша координата a впорядкованої пари (a, b) f є прообр зом (аргументом, змінною), а друга b – обр зом (значенням). Потрібно розрізняти функцію f як множину впорядкованих пар (відношення) і значення функції b = f(a) як другу координату однієї з таких пар.
Слід зазначити, що відношення, обернене до функціонального, загалом не є функціональним. У розглянутому вище прикладі відношення Q є функціональним, але
обернене йому відношення Q
-1 = {(1,1), (4,2), (4,3), (16,4)} не є функціональним.
13.Відобр ження. Види відобр жень.
Якщо функціональне відношення f А×В всюди визначене на A, то його називають відобр женням множини A в B і записують f : A → B. Очевидно, що різниця між відображенням та функцією зводиться до способу означення цих відношень на множині A, причому відображення потрібно розглядати як окремий випадок функції. Більшість математиків не розрізняють поняття відображення і функції.
При відображенні A в B кожен елемент a з A має один і тільки один образ ( a A ! b B (a = f(b)). Однак зовсім не обов’язково, щоб кожний елемент B був образом деякого елемента з A. Графічно ця ситуацію показана на рис. 3.1а. Для порівняння на рис. 3.1б наведено приклад функціонального відношення, яке не є відображенням.
Означення 3.2. Якщо для відображення f : A → B будь-який елемент b з B є образом принаймні одного елементу a з A, тобто:
b B a A : b = f(a), то кажуть, що множина A накриває множину B, а відображення буде мати назву сюр’єкції. Обернене відображення до сюр’єкції f -1 не буде порожнім.
Означення 3.3. Якщо для відображення f : A → B для будь-яких двох різних елементів a1 та a2 з A їх образи b1 та b2 також різні, то відображення f називається ін’єкцією
Іншим чином це можна записати як: b = f(a1) та b = f(a2) a1 = a2. Означення 3.4. Відображення, яке одночасно є сюр’єктивним та ін’єктивним називається бієкцією (накладанням). У цьому випадку кажуть, що між елементами A та B існує взаємно однозначна відповідність.
Якщо f – взаємно однозначне відображення, а A = B, то f : A → A називається
10
