Diskretna_Ispit_Avtosokhranenny__Avtosokhranen

Тому загальна кількість способів, якими можна вийняти одну кулю з двох урн, буде дорівнювати 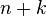. У загальному випадку правило суми може бути сформульоване таким чином.

Якщо треба виконати якусь дію n1 , n2 ,… або nk способами, то кількість можливих способів реалізації цієї дії буде дорівнювати

N = n1 +n2 +… + nk.

Особливістю цього правила є те, що воно використовує сполучник або, який протиставляє різні дії одна одній.

Правило добутку[ред. • ред. код]

П ав л використовується тоді, коли кожний елемент множини А може бути вибраний разом з елементом множини В. Відповідно до кожного способу вибору елемента множини А буде зіставлятися 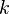способів вибору елемента множини В. Тоді загальна кількість способів

сумісного вибору елементів множини А з елементами множини В, очевидно, дорівнюватиме .

Модель урн можна застосувати і для ілюстрації правила добутку. У цьому випадку розглядаються дві урни, у першій з яких знаходиться 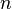куль, а в другій 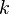. Будемо вважати, що будь-якій кулі першої урни може відповідати будь-яка куля з другої урни. А оскільки в першій урні знаходиться 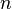куль, то й кількість способів вибору куль з першої урни разом з різними кулями з другої урни буде дорівнювати .

У загальному вигляді правило Добутку буде мати такий вигляд.

М=n1•n2 •…•nk.

Уцьому правилі важливу роль відіграє сполучник і, який об'єднує різні дії в

одну.

28.Розміщення без повторень Розміщенням з 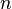елементів по 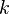називається упорядкований набір з 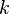різних елементів деякого 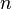-елементного безлічі.

Кількість усіх розміщень без повторень з n елементів по r позначають як

або A(n,r), де r і n – невід’ємні цілі числа, причому r≤n. Твердження 18.1. Справджується рівність =n(n-1)…(n-r+1)=

21

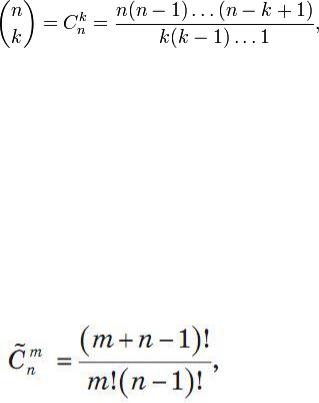
Доведення. Кожне r-розміщення є впорядкованою послідовністю завдовжки r, члени якої – попарно різні й вибираються з n-елементної множини. Тоді перший член цієї послідовності може бути вибраний n способами, після кожного вибору першого члена послідовності другий – (n–1) способами і т.д. Відповідно після кожного вибору першого, другого і т.д., аж до (r–1)-го членів послідовності r-й член може бути вибраний n − (r − )1 = n − r +1 способами, звідки за узагальненим правилом добутку дістаємо наведену вище формулу. ►

Знайдемо, наприклад, число розміщень з 7 по 3. Тут n = 7, n – r + 1 = 5. Значить

3A7

=7×6×5 = 210. Відмітимо, що верхній індекс показує яку кількість співмножників потрібно взяти у добутку.

Наслідок 1. Справджується рівність =n!

31.Комбін ції з повторенням.

Комбiнацiї з повтореннями — це сполуки, якi мають такi характернi ознаки:

1.Порядок розташування елементiв у сполуках не має значення.

2.Елементи у сполуках можуть бути задiянi вiд нуля до m разiв: 0 ≤ ki ≤ m,

де

m — кiлькiсть мiсць у кожнiй сполуцi вибраної групи;

ki — кiлькiсть мiсць у сполуцi для будь-якого елемента, що задiяний для її складання.

Кiлькiсть комбiнацiй з повтореннями обчислюють за формулою

22

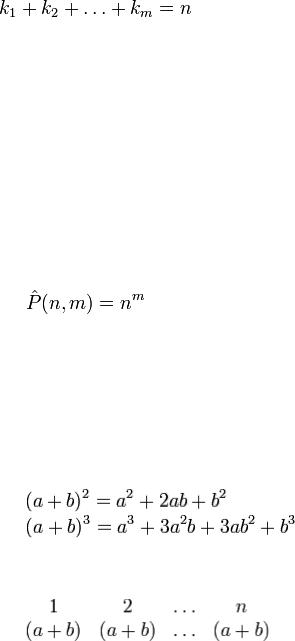
32.Перест новки з повторенням

Розглянемо n елементів m різних типів, причому в кожному типі всі елементи однакові. Тоді перестановки із всіх цих елементів з точністю до порядку

коефіцієнту

33.Розміщення з повтореннями

Розміщенням з повтореннями із n елементів

по m або в ван ю (n, m) в і ю з ве ненн називається довільний кортеж елементів множиниM, для якого |M| = n.

Кількість можливих розміщень з повтореннями із n елементів по m дорівнює n піднесене до степеня m:

Наприклад, із цифр 1, 2, 3, 4 можна скласти 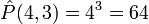трьохзначних числа.

34.Біном Ньютон . Трикутник П ск ля.

Фрмула бінома Ньютона із степенями n=2 та 3:

Спробуємо розкласти (a+b)n в многочлен у загальному випадку n. Запишемо його у вигляді добутку, пронумерувавши дужки:

Кожний доданок містить n множників: k множників a і (n-k) множників b, тобто має вигляд akbn-k, де k≤n, k≥0. Кожний такий доданок взаємно однозначно відповідає підмножині номерів дужок, з яких для утворення цього доданка, бралися множники a. Таким чином, доданків 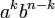рівно стільки, скільки таких підмножин.

23

Вкомбінаториці це число називається числом комбінацій з n по k і

позначається 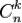або 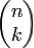. Отже,

Коефіцієнти при 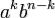називаються біноміальними, оскільки записуються в розкладі бінома (a+b)n.

Біноміальні коефіцієнти мають очевидну властивість симетрії:

Розглянемо окремі випадки бінома Ньютона:

при b=1 маємо :,

при a=b=1 маємо :,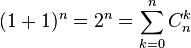

при a= −1, b=1 маємо :.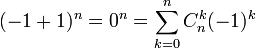

Запишемо біноміальні коефіцієнти для початкових значень n=0, 1, …, 5 у трикутну таблицю (трикутник Паскаля):

З таблиці видно, що кожний елемент, який не є першим у своєму рядку, є сумою елемента над ним і елемента, розташованого над ним і ліворуч:

.

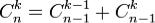Доведення цього факту можливе методом математичної індукції.

35. Вл стивості біномі льних коефіцієнтів.

24

Основні властивості біноміальних коефіцієнтів

1. Формула симетрії

Cmn=Cn−mn

2. Формула додавання

Cmn+Cm+1n=Cm+1n+1

3. Формула суми всіх біноміальних коефіцієнтів

∑k=0nCkn=2n

4. Формула винесення за дужки

Ckn=nk Ck−1n−1

25