Відображення метричних просторів

Границя і неперервність. Критерій неперервності.

Нехай маємо два метричних простори (X,ρ_x), (Y,ρ_y) і множину Е(X,ρ_x).

Означення. Якщо кожному елементу поставлено у відповідність цілком певний елементу із простору (Y,ρ_y), то кажуть, що задано відображення множини Е в простір (Y,ρ_y) та позначають: або y=Ax.

Поняття відображення є узагальненням поняття функції. Це може бути числова функція однієї змінної, багатьох змінних, функціонал. У функціональному аналізі відображення, яке елементу довільної природи х ставиться у відповідність елемент довільної природи у, прийнято ще називати оператором.

Приклади.

1) ;

2)

3) – функціонал;

4)

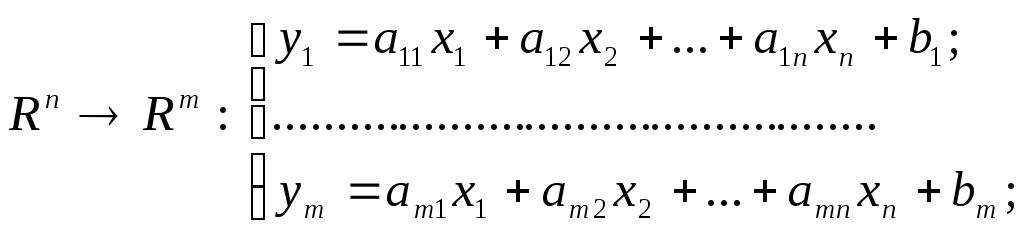
5)

6) Розглянемо многочлен Бернштейна: Це відображення кожній неперервній функції ставить у відповідність многочлен Бернштейна. Функція задається на сегменті [0,1]. Особливість многочлена Бернштейна в тому, що він може наблизити як завгодно точно будь-яку неперервну функцію на [0,1].

За рахунок степеня многочлена n, можна досягти того, що різниця між функцієюі многочленом Бернштейна буде як завгодно мала.

Нехай x₀ – гранична точка множини Е, і вона не обов’язково належить множині Е, яка входить у простір (X,ρ_x).

Означення (за Коші). Елемент А, який належить простору (Y,ρ_y) називається границею відображення при, якщо длятаке що, як тількито.

Означення (за Гейне). Елемент А називається границею відображення при, якщо із збіжності будь-якої послідовностівипливає збіжність відповідної послідовності значень відображеннядоА. (Тут збіжність розуміється як збіжність за відстанню).

Нехай тепер відображення визначене в точці x₀.

Означення. Відображення називаєтьсянеперервним у точці x₀, якщо для , що як тількито.

Означення. Відображення називаєтьсянеперервним в точці x₀, якщо із збіжності будь-якої послідовності випливає збіжність.

Якщо відображення взаємооднозначне, то для нього існує обернене відображення.

Означення. Взаємнооднозначне і неперервне відображення називається гомеоморфізмом.

Означення. Гомеоморфне відображення називається ізометрією, або ізоморфізмом, якщо воно зберігає відстань між образами.

Теорема (критерій неперервності). Щоб відображення було неперервним необхідно і достатньо, щоб прообразбув відкритим для всякої відкритої множиниG, яка входить в Y.

Доведення. Необхідність. Дано, що відображення – неперервне і множинаG – відкрита. Треба довести, що – відкрита, тобто всі її точки внутрішні. Нехай,. Покажемо, що точкаx₀ належить множині разом з своїм околом. Оскількиy₀ є внутрішньою точкою множини G, то існує , що куля. В силу неперервності відображення по заданому ми знайдемо таке , що як тількипопадає в кулю , тоy попадає в кулю . Ясно, що куляналежить множині праобразів, це означає, щоразом із деяким своїм околом, а це означає, щоє відкритою множиною (в силу довільності вибраної точкиx₀).

Достатність. Дано – відкрита куля, для будь-якої відкритої множини. Доведемо неперервність відображення. Нехай– довільна точка множиниі нехай. Длярозглянемо кулю. За умовою образ даної кулі:– є відкрита множина, тобто всі її точки внутрішні, а отже і точка, це означає, що знайдеться таке, що куляпопаде в кулю, а це і означає неперервність даного відображення у точціx₀ за Коші.

Теорему доведено.

Зв’язність та її збереження при неперервному відображенні.

Означення. Множина Е називається зв’язною, якщо її не можна подати у вигляді об’єднання двох відкритих множин, що не перетинаються.

Теорема. Образ зв’язної множини при неперервному відображенні є множина зв’язна.

Доведення. Дано – зв’язна. Треба довести– зв’язна. Нехай – не зв’язна, і її подано у вигляді об’єднання двох відкритих множин, які не перетинаються. Позначимо їх через Е₁ та Е₂. Але за критерієм неперервності прообраз множини Е₁ – відкрита множина, і прообраз Е₂ – також відкрита. Позначимо їх G₁ та G₂ , вони не будуть перетинатися (в силу неперервності відображення). Тобто множину праобразів ми подали у вигляді об’єднання двох відкритих множин, що не перетинаються , а це суперечить тому, що G – зв’язна. Отже образ – є множина зв’язна.

Теорему доведено.