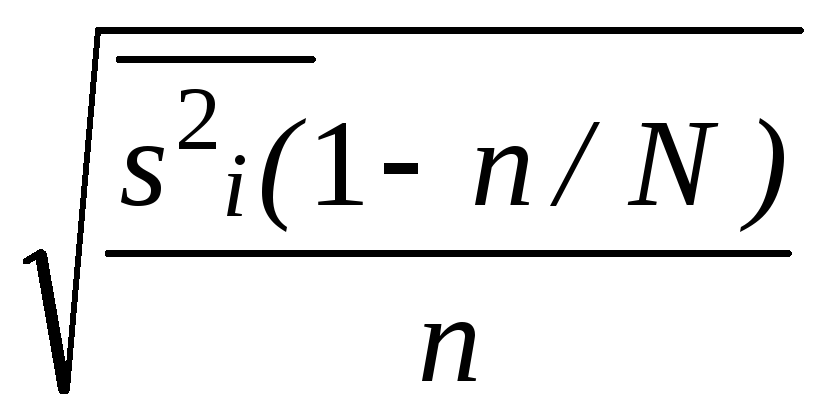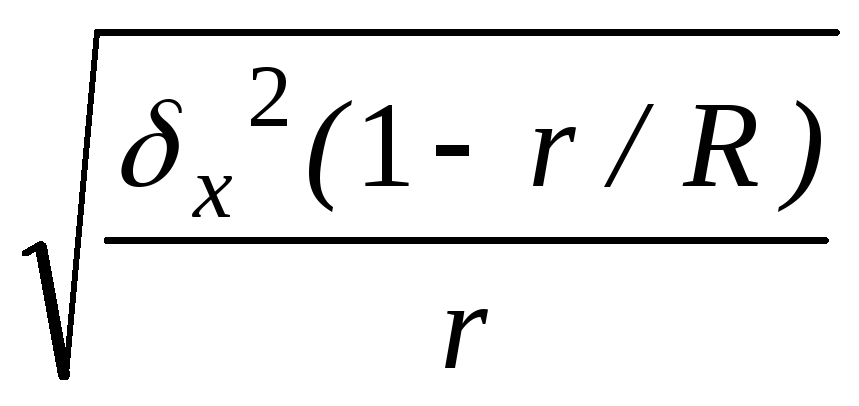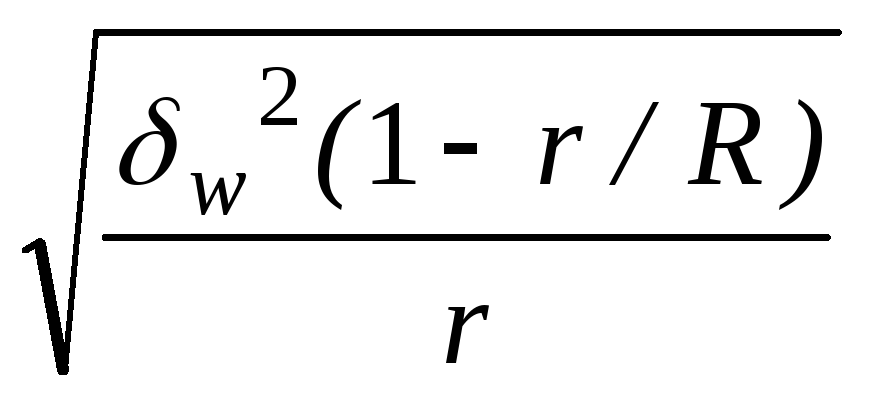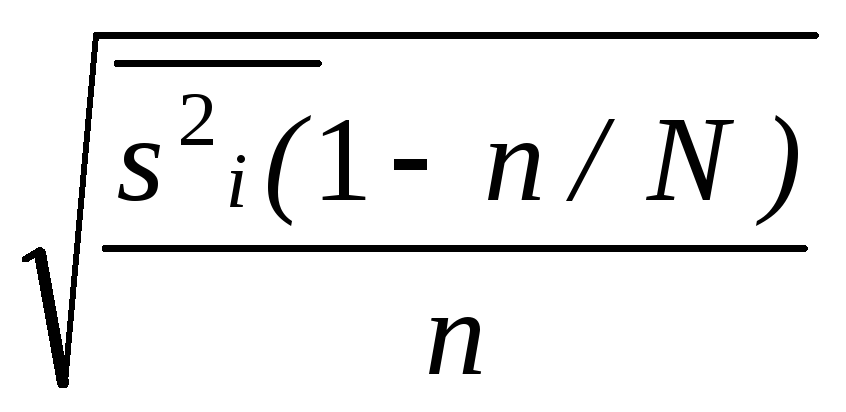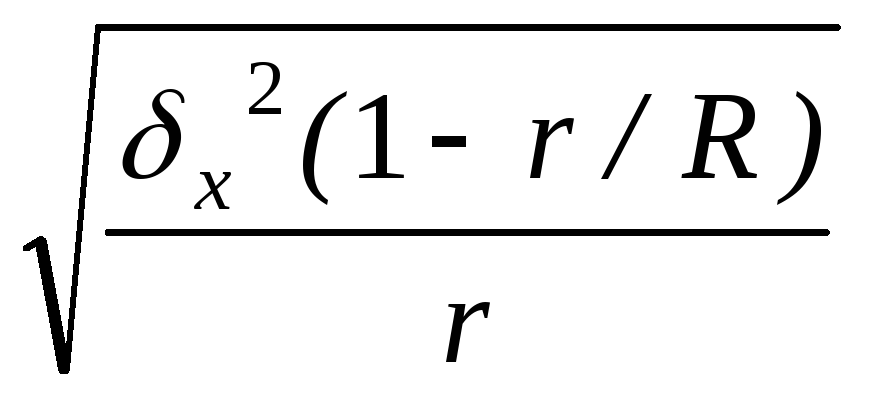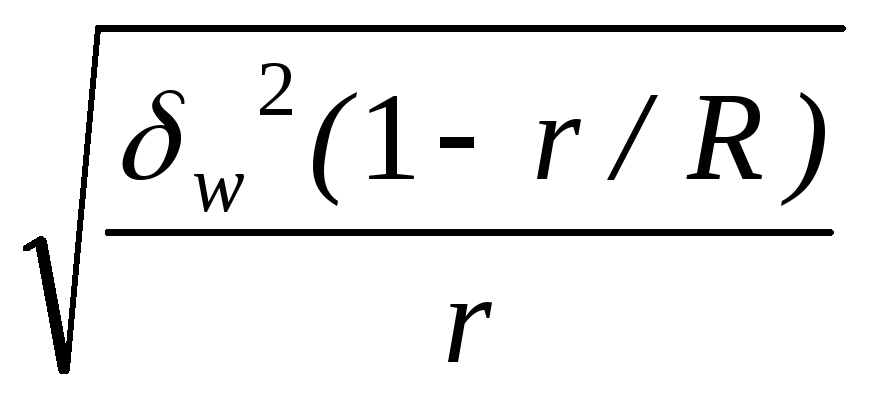шпаргалка по статистике
.docКорреляция
-
Коэффициент парной корреляции знаков Фехнера
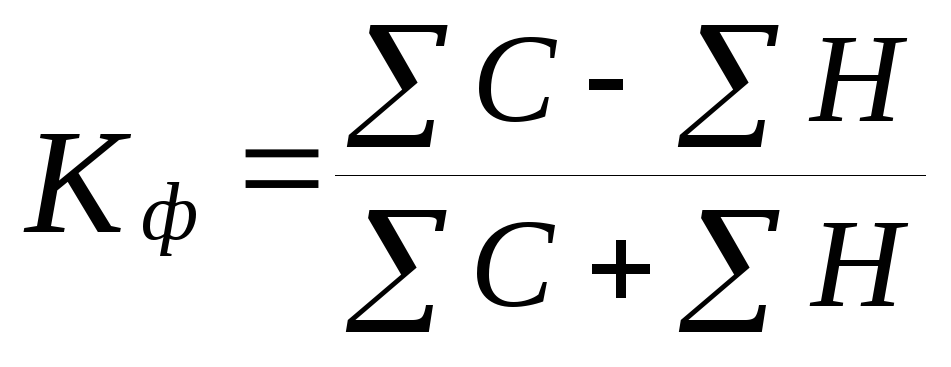
-
Коэффициент парной корреляции Пирсона rху=rух=
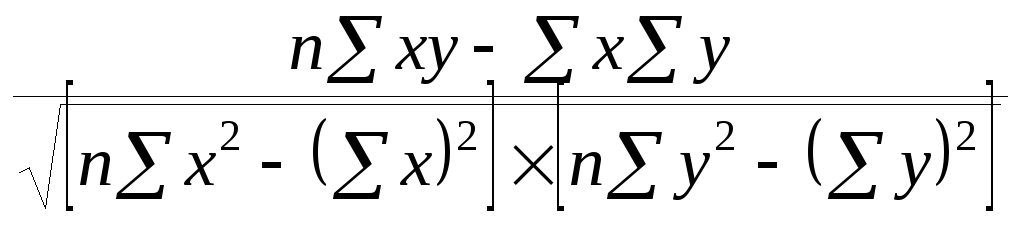
-
Коэффициент множественной (совокупной) линейной корреляции Пирсона
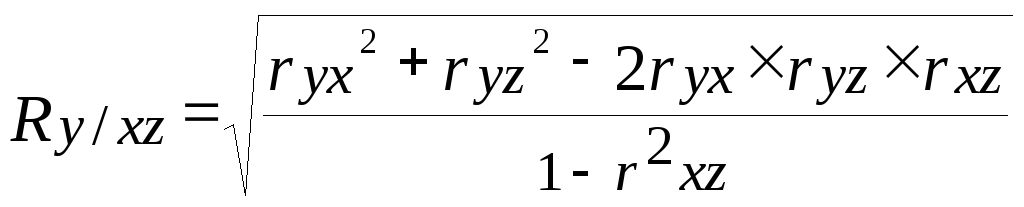
-
Чистый (частный) коэффициент линейной корреляции Пирсона
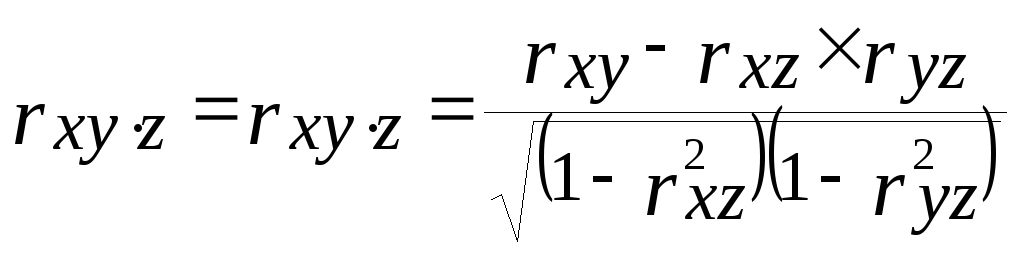
-
Квадраты коэффициентов корреляции (2)–(3) называются коэффициентами (индексами) детерминации
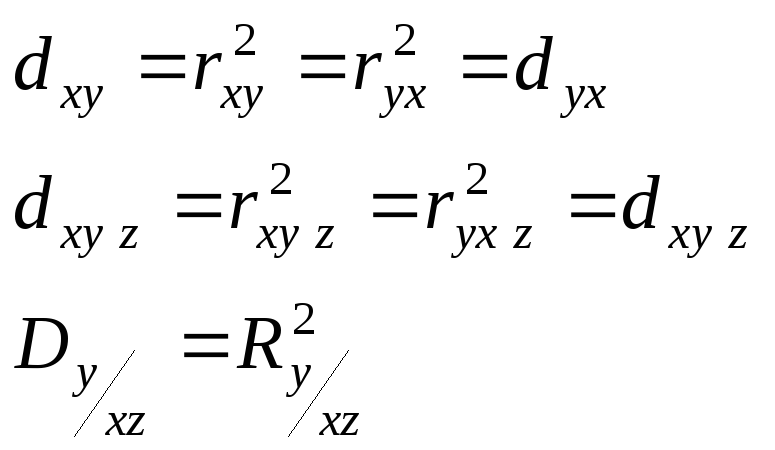
-
Значимость парного и чистого (частного) коэффициентов корреляции Пирсона проверяется в случае нормальности их распределения, на основании t-распределения с заданным уровнем вероятностной значимости и имеющейся степени свободы
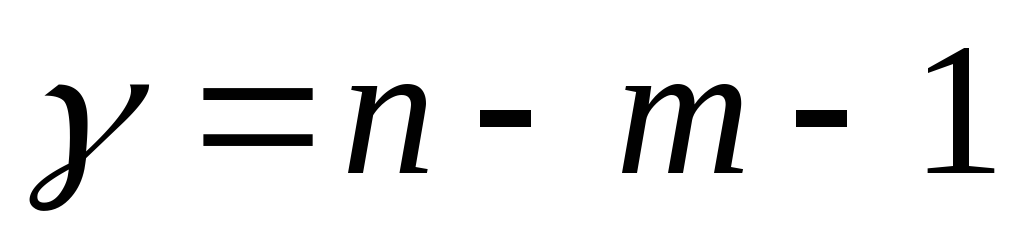 ,
где m – число связей
(факторных переменных). Для парного
коэффициента rху
имеем его среднеквадратическую ошибку
,
где m – число связей
(факторных переменных). Для парного
коэффициента rху
имеем его среднеквадратическую ошибку
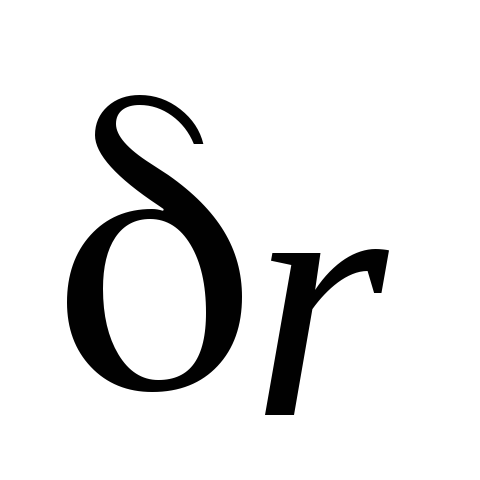 и фактическое значение t-критерия
Стьюдента
и фактическое значение t-критерия
Стьюдента
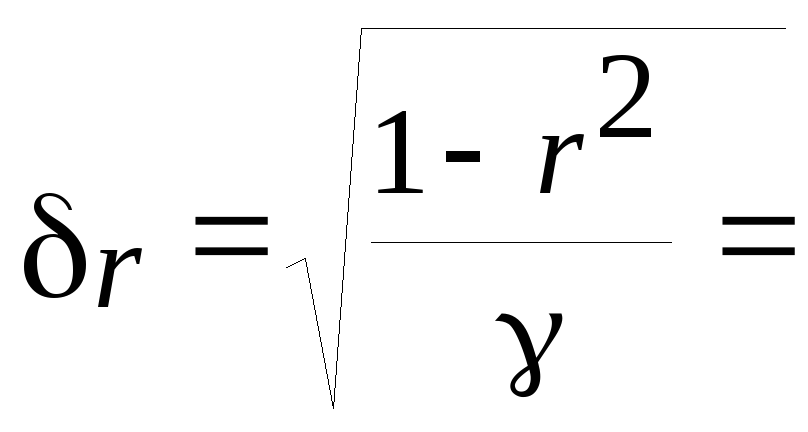
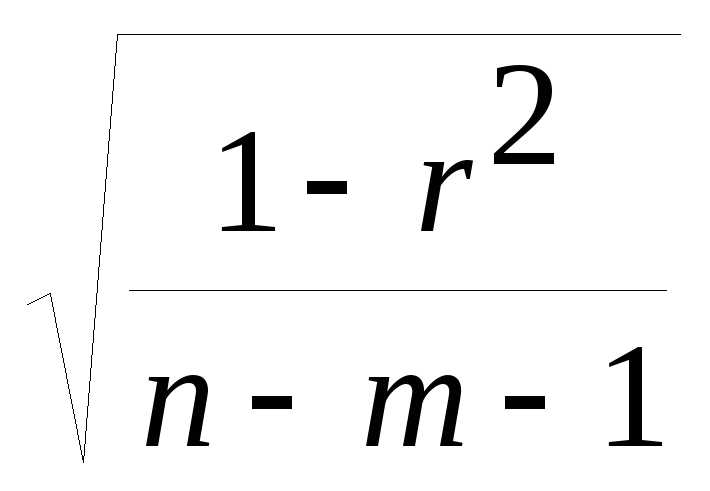 =
=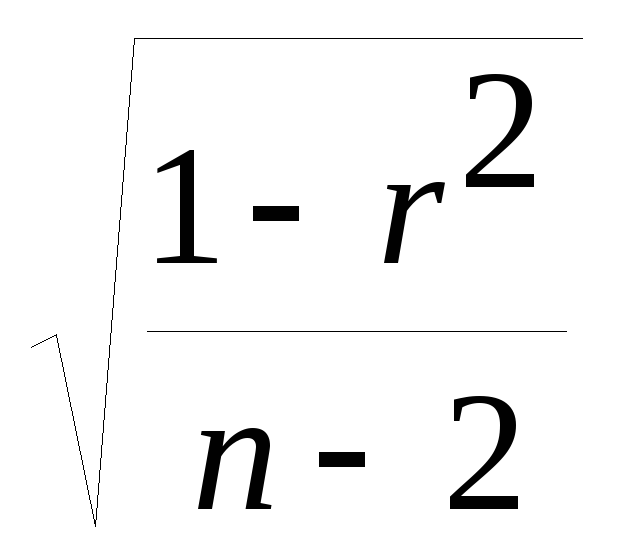 ;
;
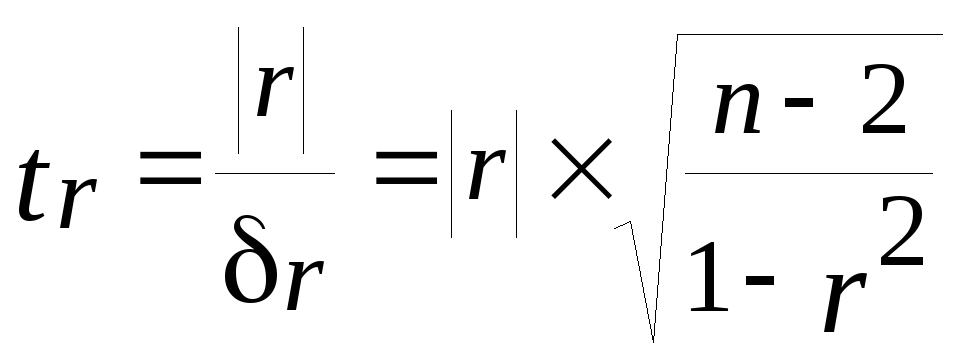 Если tr
> tтабл. , то
коэффициент парной корреляции – общий
или чистый является статистически
значимым, а при tr
≤ tтабл. –
незначимым.
Если tr
> tтабл. , то
коэффициент парной корреляции – общий
или чистый является статистически
значимым, а при tr
≤ tтабл. –
незначимым. -
Ранговые коэффициенты парной линейной корреляции
 и
и
 Спирмэна и Кендэла. В случае
неповторяющихся (несвязных) рангов
Спирмэна и Кендэла. В случае
неповторяющихся (несвязных) рангов
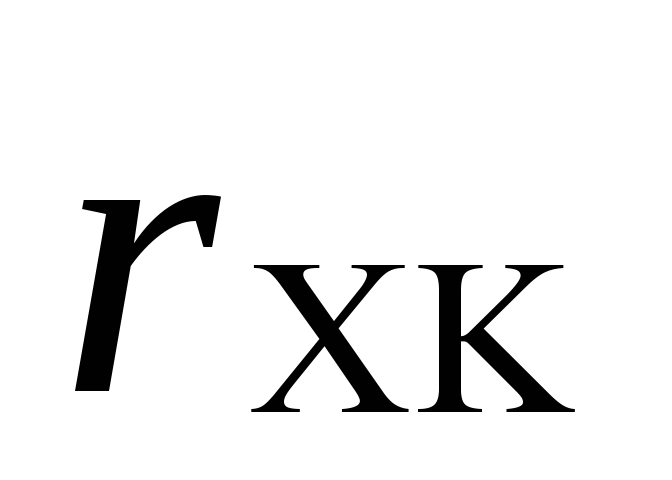 и
и
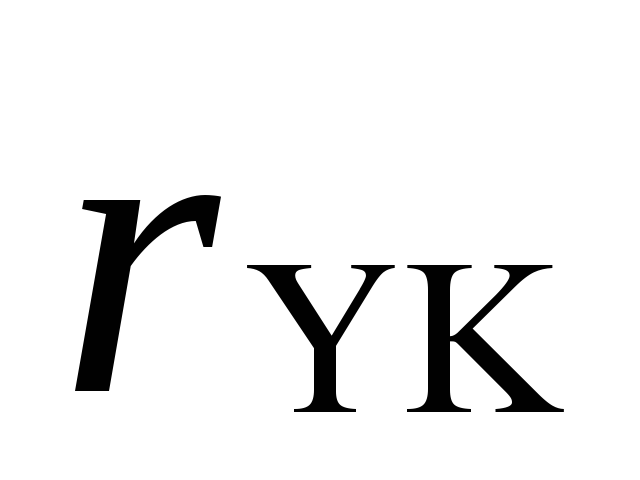 для переменных xк и yк
в их наблюдениях к=
для переменных xк и yк
в их наблюдениях к=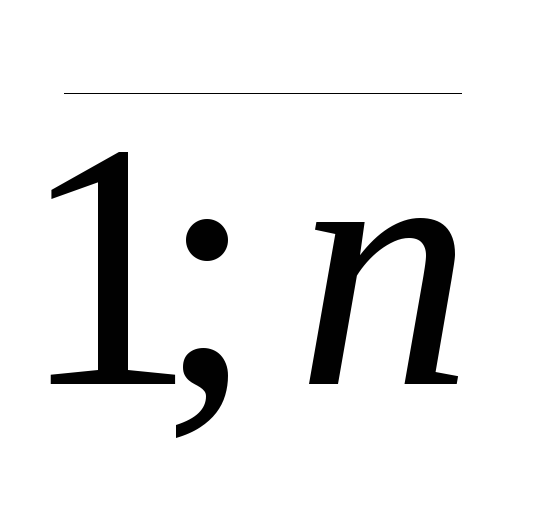 искомые ранговые коэффициенты равны:
а)
искомые ранговые коэффициенты равны:
а)
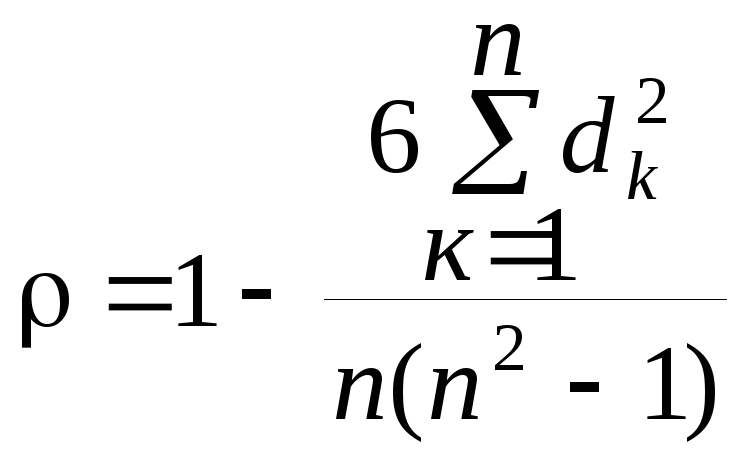 ;
;
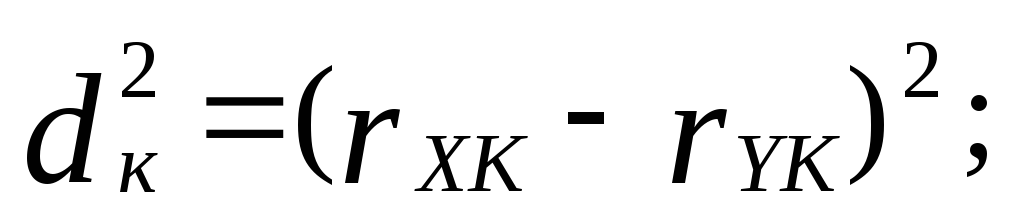 -1
-1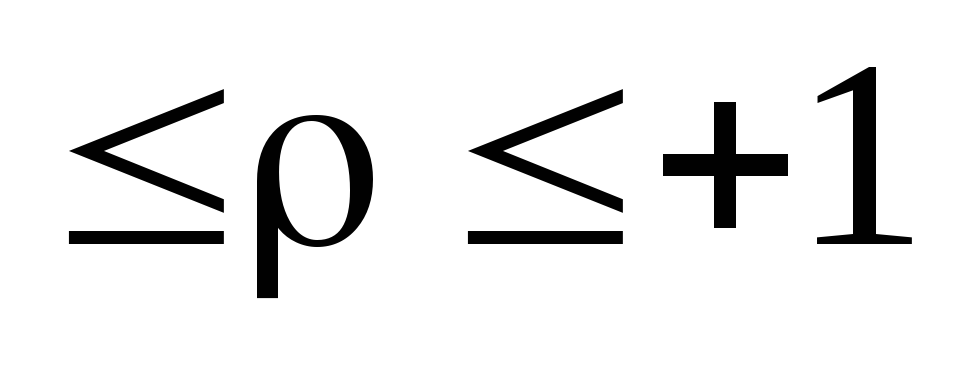 ;
;
 ;
;
б)
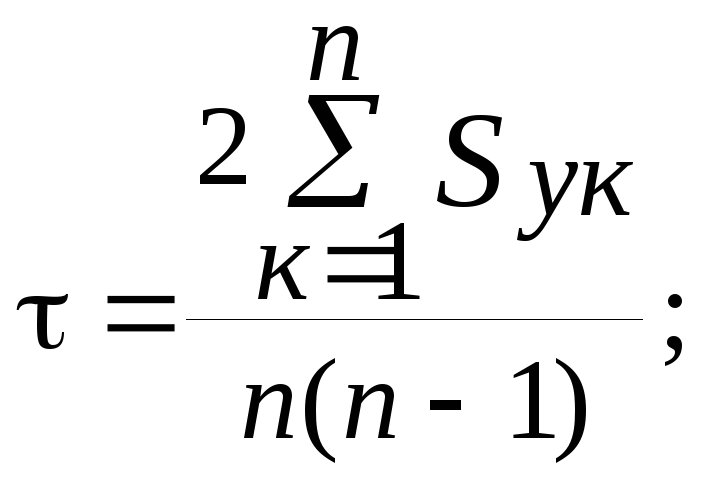
![]() -1
-1![]() ;
;![]() dк2 –
квадрат разности рангов
dк2 –
квадрат разности рангов
![]() и
и
![]() двух переменных x и y
в наблюдении к
двух переменных x и y
в наблюдении к![]() – число рангов
– число рангов
![]() превышающих данный ранг
превышающих данный ранг
![]() зависимой переменной у при сравнении
ее наблюдения К;
зависимой переменной у при сравнении
ее наблюдения К;
![]() – число рангов
– число рангов
![]() превышающих данный ранг
превышающих данный ранг
![]() зависимой переменной у при сравнении
ее наблюдения к со всеми последующими
наблюдениями к + i
для i =
зависимой переменной у при сравнении
ее наблюдения к со всеми последующими
наблюдениями к + i
для i =
![]()
![]() – аналогичное число последующих рангов,
не превышающих данный ранг
– аналогичное число последующих рангов,
не превышающих данный ранг
![]() ;
;
![]() – сумма превышающих и непревышающих
рангов.
– сумма превышающих и непревышающих
рангов.
8. Коэффициент линейной конкордации
(экспертного согласия) Кендэла –
коэффициент множественной ранговой
корреляции
![]() ;
S=
;
S=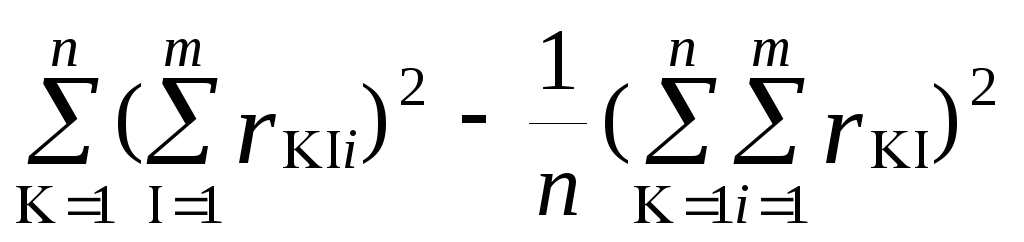 ;
;
![]()
9. Значимость коэффициентов Спирмэна и
Кендэла: критерий Стьюдента
![]() :
:![]()
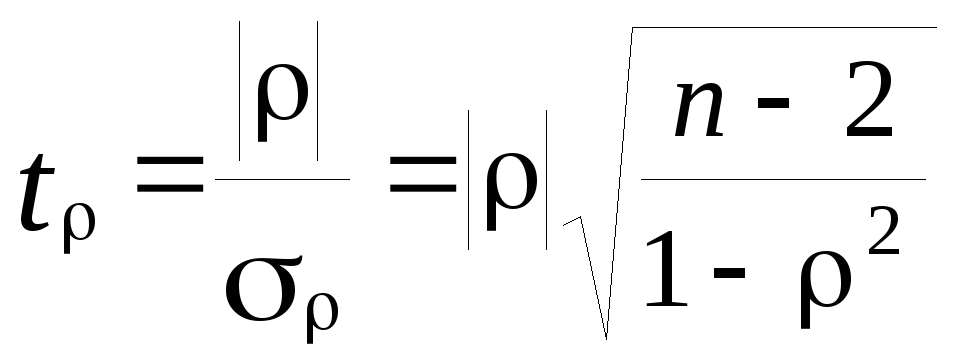 .
Если
.
Если
![]() ,
то коэффициент
статистически значим с заданным уровнем
значимости и
имеющейся степенью свободы
,
то коэффициент
статистически значим с заданным уровнем
значимости и
имеющейся степенью свободы
![]()
![]() .
.
10. Корреляция качественных признаков
-
Коэффициент ассоциации Юла
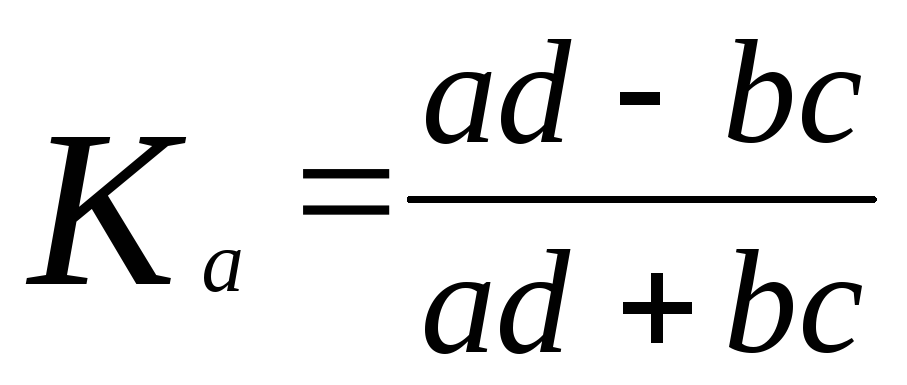
-
Коэффициент контингенции Пирсона )
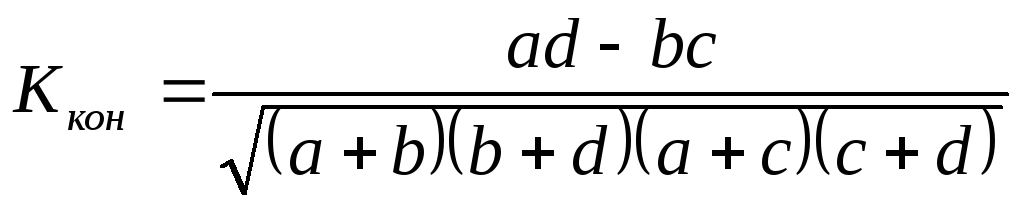
-
Коэффициент взаимной сопряженности Пирсона а) С=
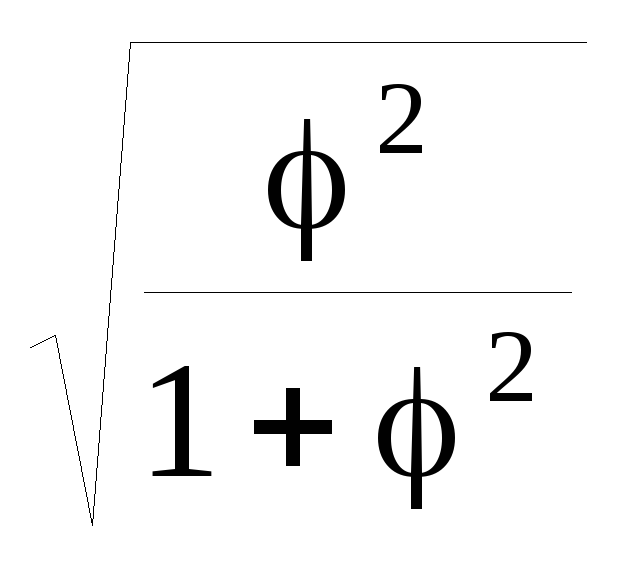 ;
;
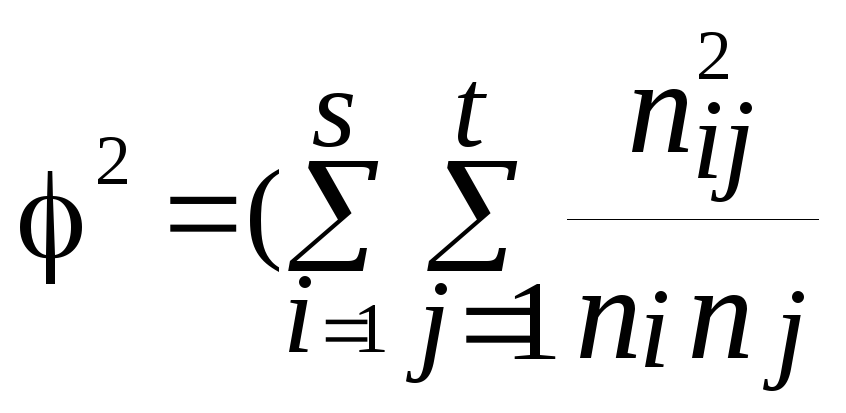 )
– 1;
)
– 1;
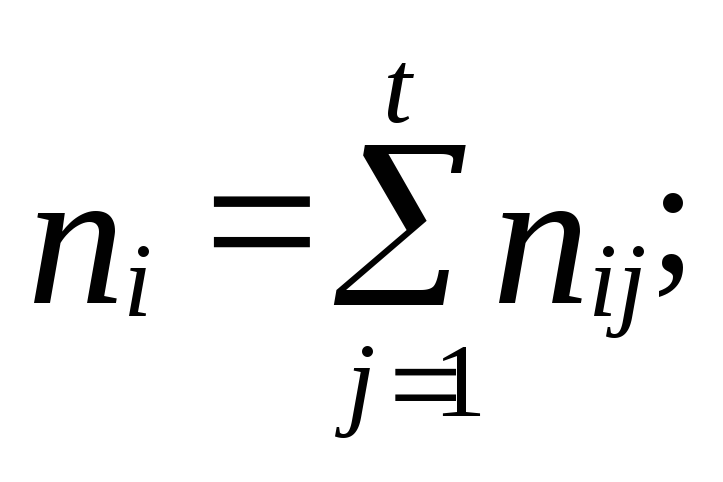
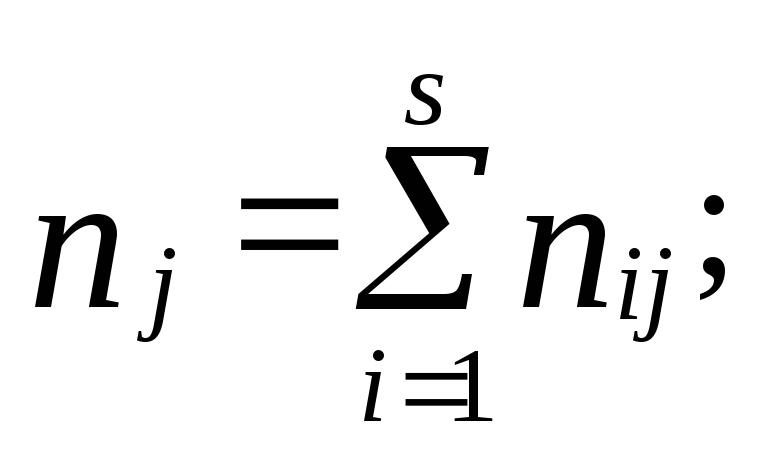
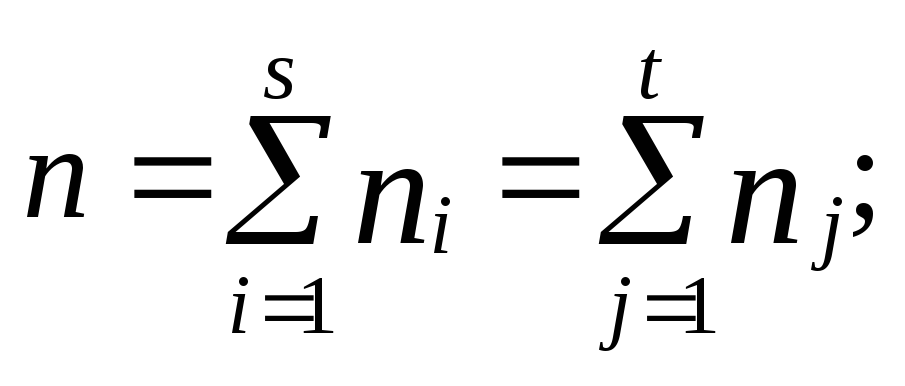 0
0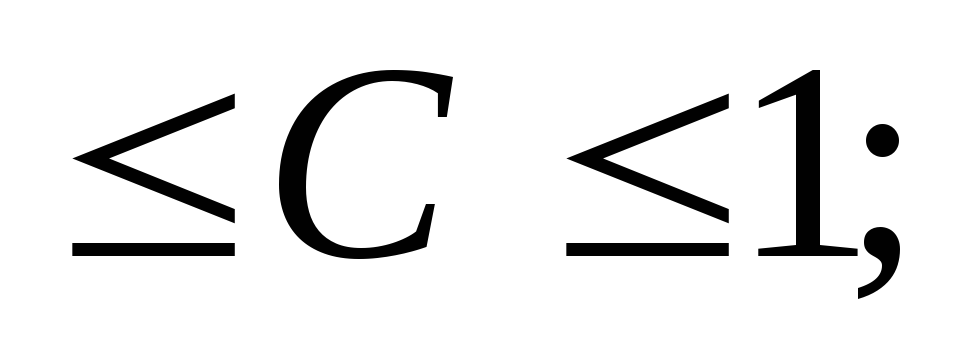
Коэффициент взаимной сопряженности
Чупрова Т=![]() 0
0![]() .
.
![]() – показатель "средней квадратической
сопряженности" (по Пирсону) как общая
сумма отношений квадратов клеточных
частот к произведению их маргинальных
(итоговых) частот за вычетом из этой
суммы единицы.
– показатель "средней квадратической
сопряженности" (по Пирсону) как общая
сумма отношений квадратов клеточных
частот к произведению их маргинальных
(итоговых) частот за вычетом из этой
суммы единицы.
Ряды динамики
-
Средний уровень в интервальных рядах динамики
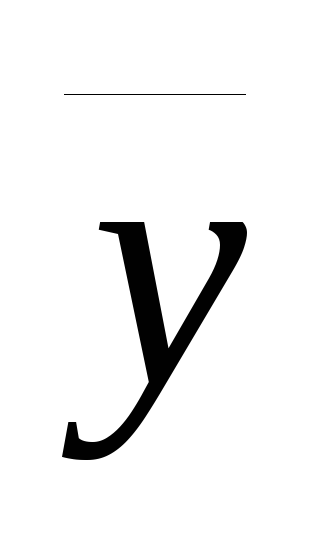 =
=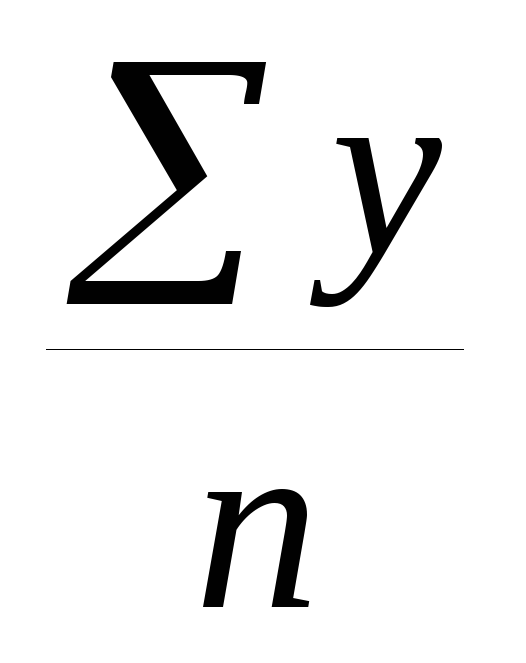 ,
, -
Моментные ряды динамики
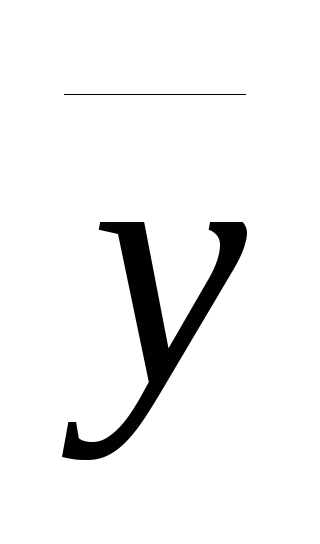 =
=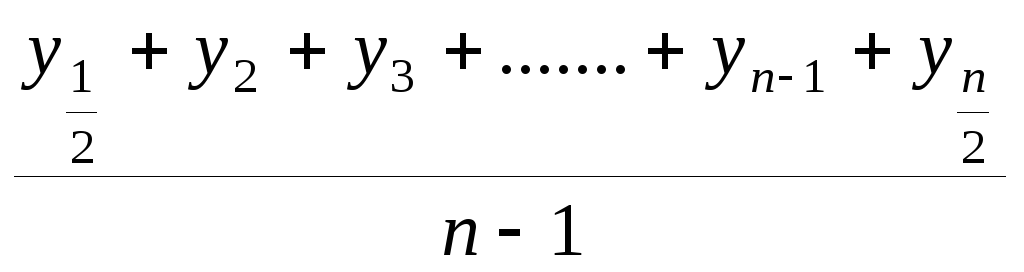 n
–число моментов (уровней ряда); n
– 1 – число
периодов времени (лет, кварталов,
месяцев).
n
–число моментов (уровней ряда); n
– 1 – число
периодов времени (лет, кварталов,
месяцев). -
С неравными интервалами времени
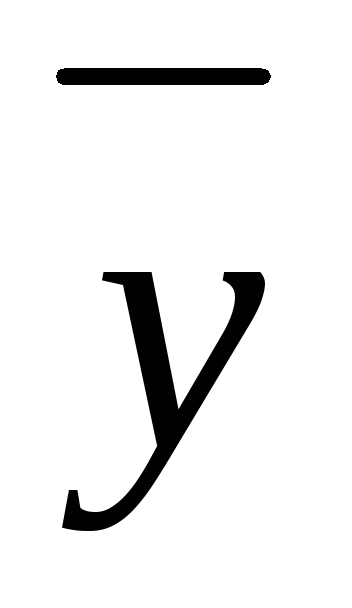 =
=
-
Когда конкретные даты изменения показателя неизвестны,
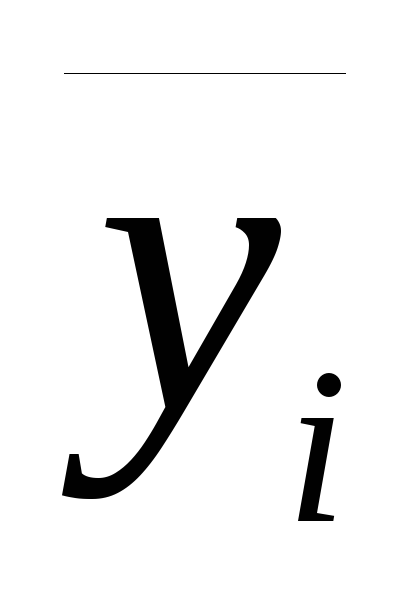 =
=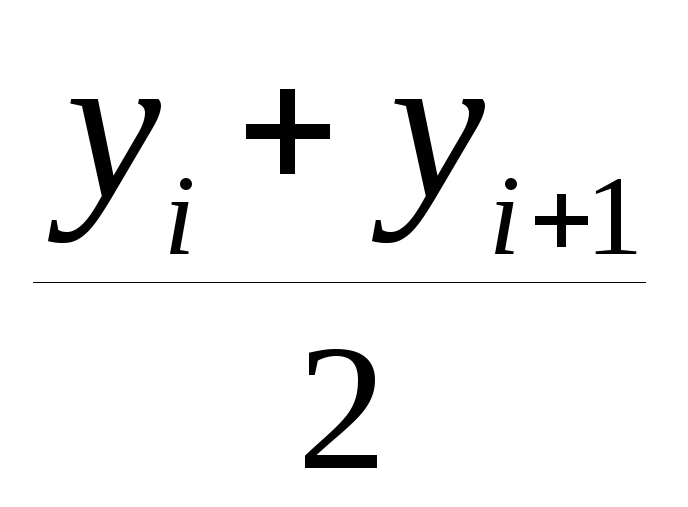 ;
;
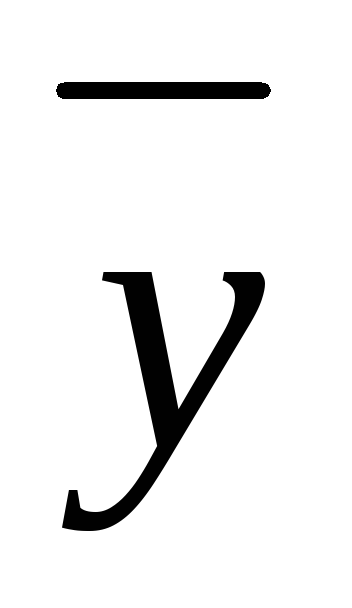 =
=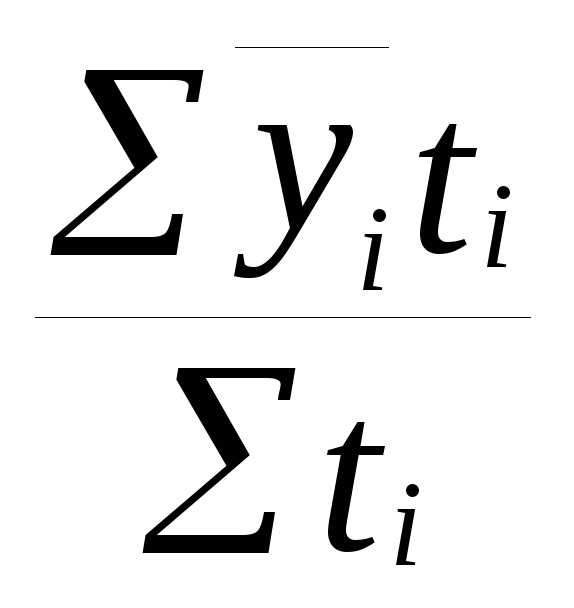
-
Средний уровень в производных рядах средних величин
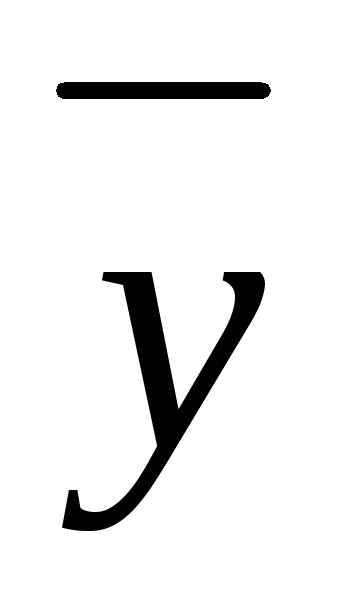 =
=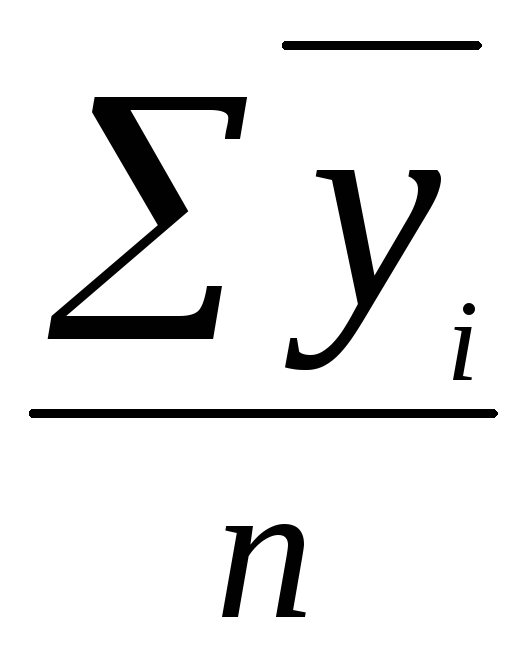
-
Абсол. прирост, темпы и к-ты (при)роста
-
Индекс сезонности исчисляется путем деления средних величин за каждый месяц на общую среднюю месячную величину, принятую за 100%
-
Методы выравнивания рядов динамики
-
метод укрупнения интервалов (простая средняя)
-
метод скользящей средней;
-
метод аналитического выравнивания (Ур-е регрессии) ;
Выборка
-
Доля выборки kn = n/N.
-
Выборочная доля w = nn/n.
-
Средняя ошибка выборки есть величина m =
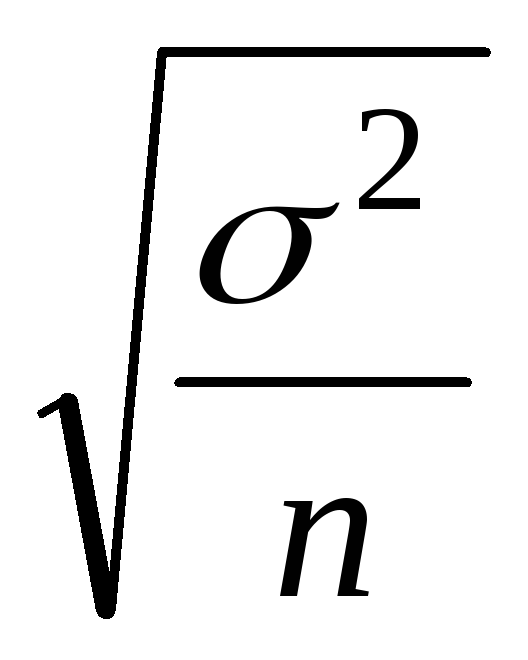 ,
выражающая среднее квадратическое
отклонение выборочной средней от
математического ожидания
,
выражающая среднее квадратическое
отклонение выборочной средней от
математического ожидания -
2 = s2
 ,
, -
Средняя ошибка (m) выборочных средней (x) и доли (р) для разных видов выборки
|
Вид выборки |
Отбор |
|
|
Повторный |
Бесповторный |
|
|
Количественный признак |
||
|
Собственно-случайная |
mx
= |
mx
= |
|
Механическая |
– |
-"- |
|
Типическая (стратифицированная) |
mx
= |
mx
= |
|
Серийная |
mx
= |
mx
= |
|
Альтернативный признак |
||
|
Собственно-случайная |
mp
=
|
mp
=
|
|
Механическая |
- |
-"- |
|
Типическая (стратифицированная) |
mp
=
|
mp
=
|
|
Серийная |
mx
=
|
mx
=
|
Где ![]() –
средняя из внутригрупповых выборочных
дисперсий для непрерывного признака;
–
средняя из внутригрупповых выборочных
дисперсий для непрерывного признака;
![]() – средняя из внутригрупповых дисперсий
доли;
– средняя из внутригрупповых дисперсий
доли;
r – число отобранных серий, R – общее число серий;
![]() =
=![]() ,
,
гдеxi* – средняя i-й серии;
x – общая средняя по всей выборочной совокупности для непрерывного признака;
![]() =
=![]() ,
,
где wi * – доля признака в i-й серии;
w – общая доля признака по всей выборочной совокупности.
6.
ОШИБКА – ВЕРОЯТНОСТЬ
Значения функции Ф(t) при некоторых значениях t равны:
|
t |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
|
Ф(t) |
0,683 |
0,866 |
0,954 |
0,98 8 |
0,997 |
0,999 |
Предельная ошибка () выборки для средней (x) и доли (р) для разных видов выборочного наблюдения
|
N |
Вид выборки |
Отбор |
|
|
повторный |
бесповторный |
||
|
1 |
2 |
3 |
4 |
|
Количественный признак |
|||
|
1 |
Собственно-случайная |
t
|
t
|
|
2 |
Механическая (n ) |
– |
-"- |
|
3 |
Типическая (стратифицированная) |
t
|
t
|
|
4 |
Серийная |
t
|
t
|
|
1 |
2 |
3 |
4 |
|
Альтернативный признак |
|||
|
5 |
Собственно-случайная |
t
|
t |
|
6 |
Механическая (n) |
– |
-"- |
|
7 |
Типическая (стратифицированная) |
t
|
t
|
|
8 |
Серийная |
t
|
t
|
ИНДЕКСЫ
-
Индивидуальные индексы
Физического объема товарооборота
цен
товарооборота
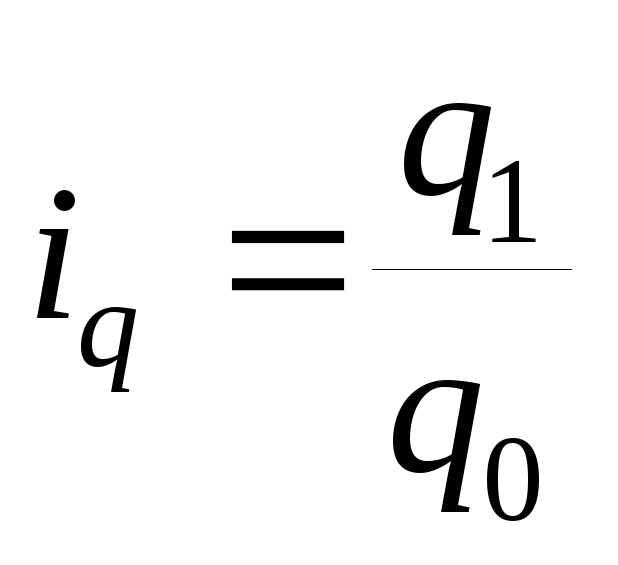

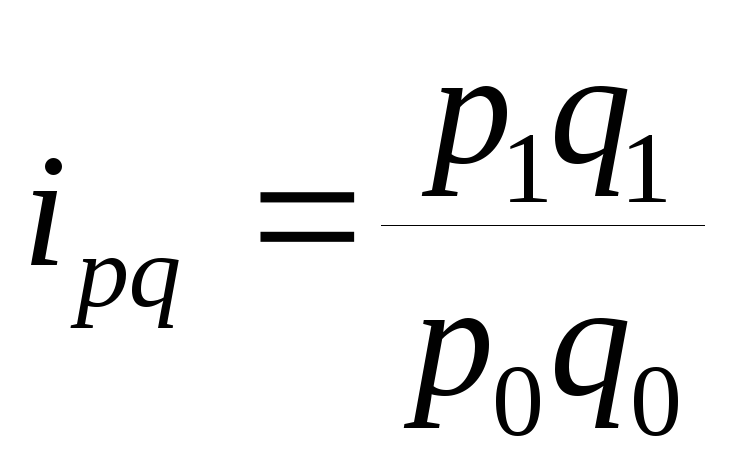
-
Общий индекс товарооборота по формуле:
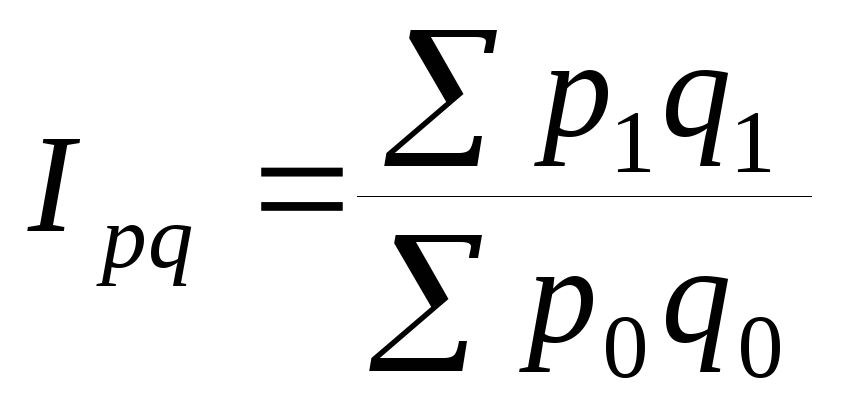
-
Общий индекс физического объема товарооборота по формуле:
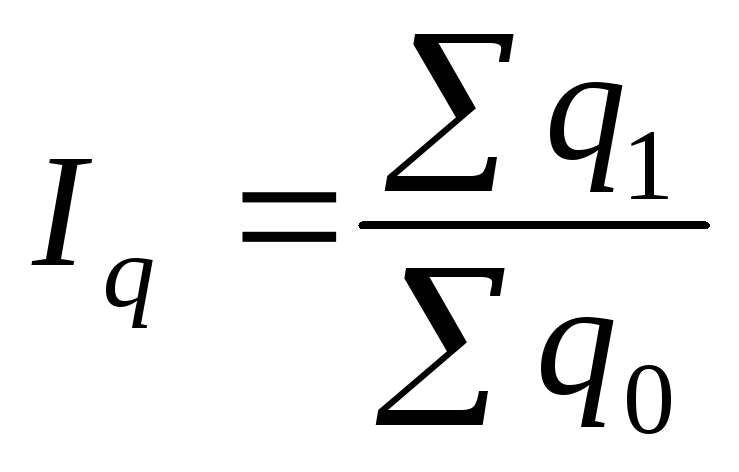 ,
, -
Индекс физического объема товарооборота должен показать изменение количества проданных разнородных товаров
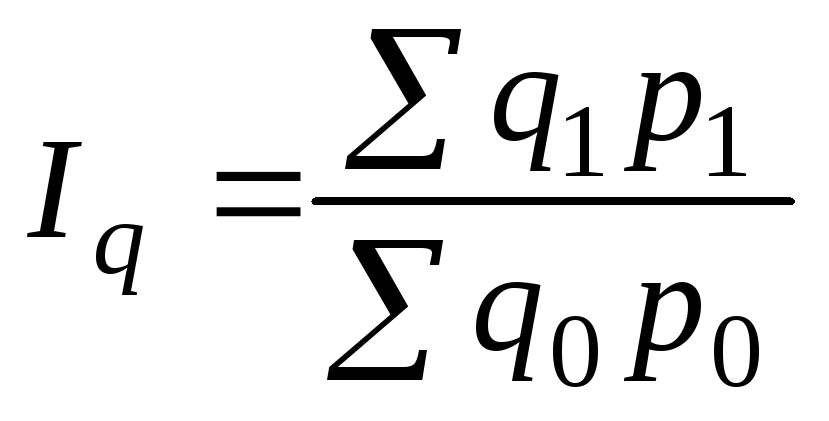
-
Агрегатный индекс цен немецкого экономиста Э. Пааше:
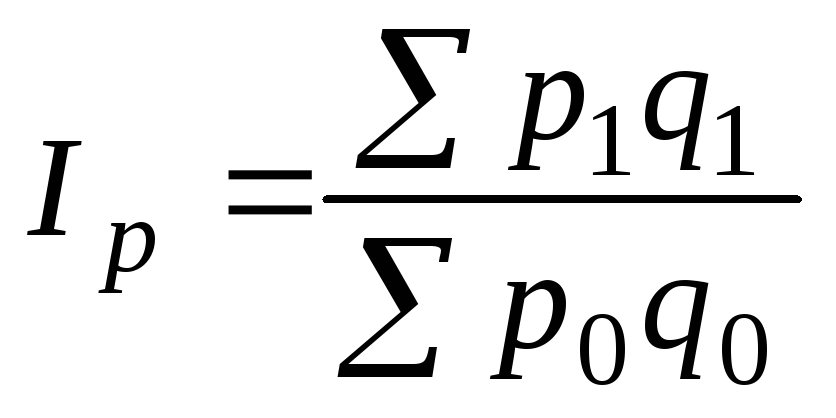 .
. -
Индекс цен, построенный с базисными весами Э. Ласпейреса:
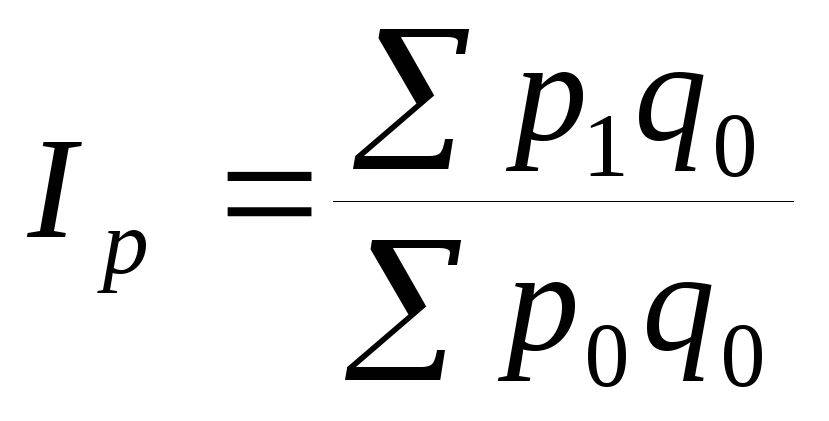 .
. -
Средние индексы применяются в том случае, когда в исходной информации нет данных для расчета индексов в агрегатной форме. Получают средний индекс путем замены в исходном агрегатном индексе индексируемого показателя его выражением, выведенным из индивидуального индекса. Если такая замена произведена в числителе исходного агрегатного индекса, то получим средний арифметический индекс, а если в знаменателе, то – средний гармонический индекс.
-
Средний арифметический индекс физического объема товарооборота:
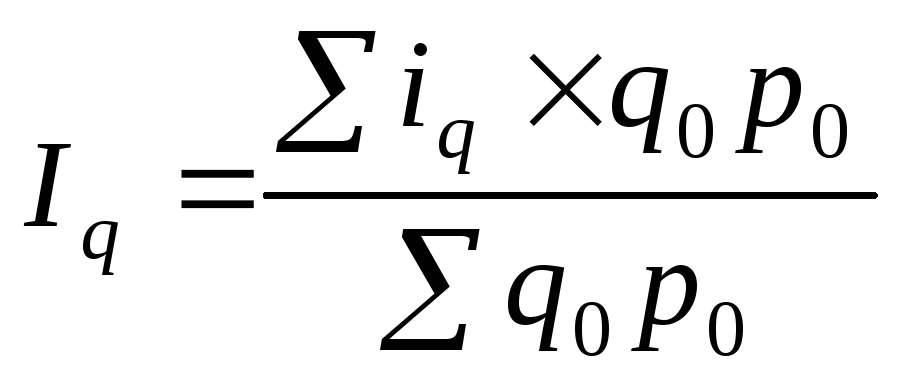 .
.