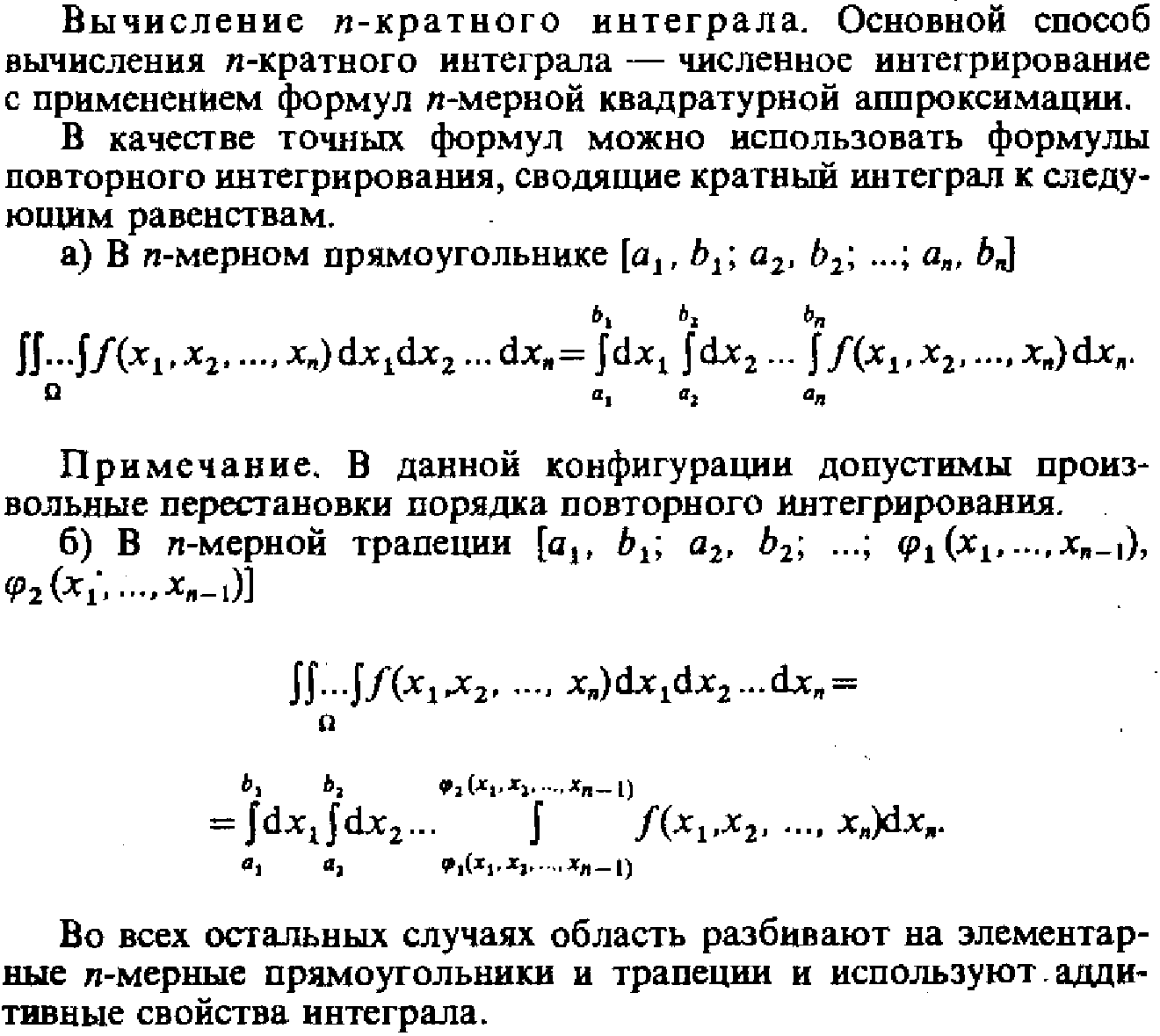Ответы на вопросы к экзамену

1. Понятие о функциях и способах их задания:

у наз.ф-цией от х , если каж.рассматр знач-ю х соотв.опред.знач-е величины у

х-аргумент,у-ф-ция. Способы задания:а)аналитический б)графический в)табличный

2. Классификация функций

Заданные аналитически:1)алгебраические-получены в рез-те алгебраич.действий над знач-ми аргумента(многочлен) 2)неалгебраические(логафифм, тригонометрические)

Обратные ф-ции-получ.ф-ной зависимостью у=f(х) но у-аргумент, х-ф-ция

3. Пределы. Понятия о пределах послед-тей и ф-ций

4. Непрерывность и разрыв ф-ций

5. Бесконечно малые ф-ции

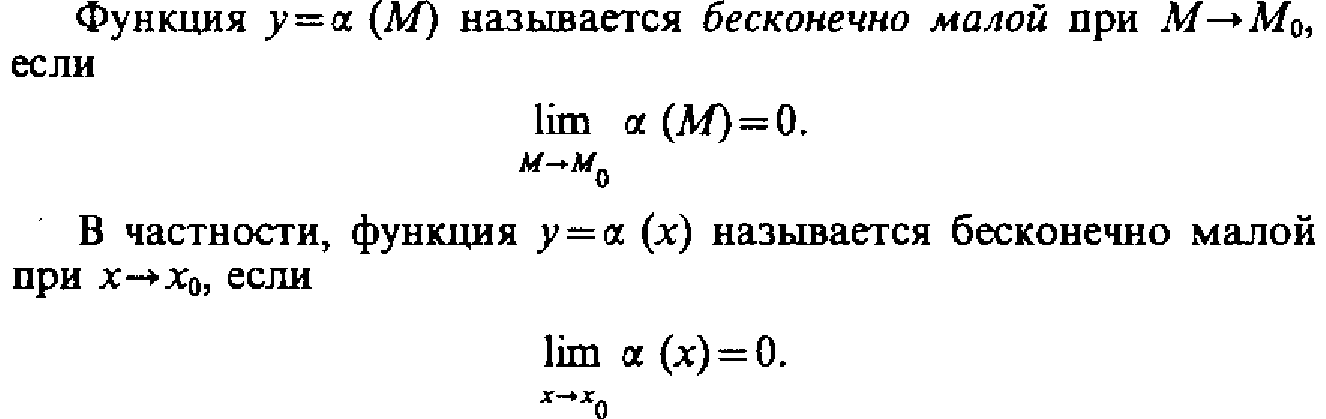
5. Теоремы о пределах

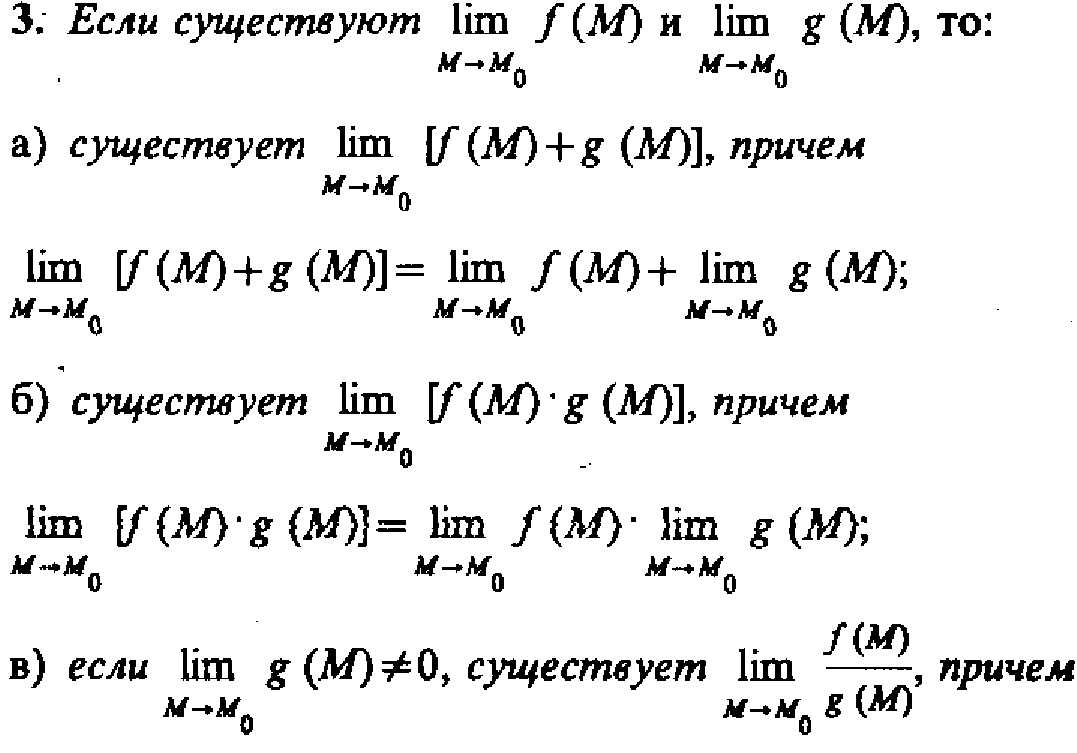
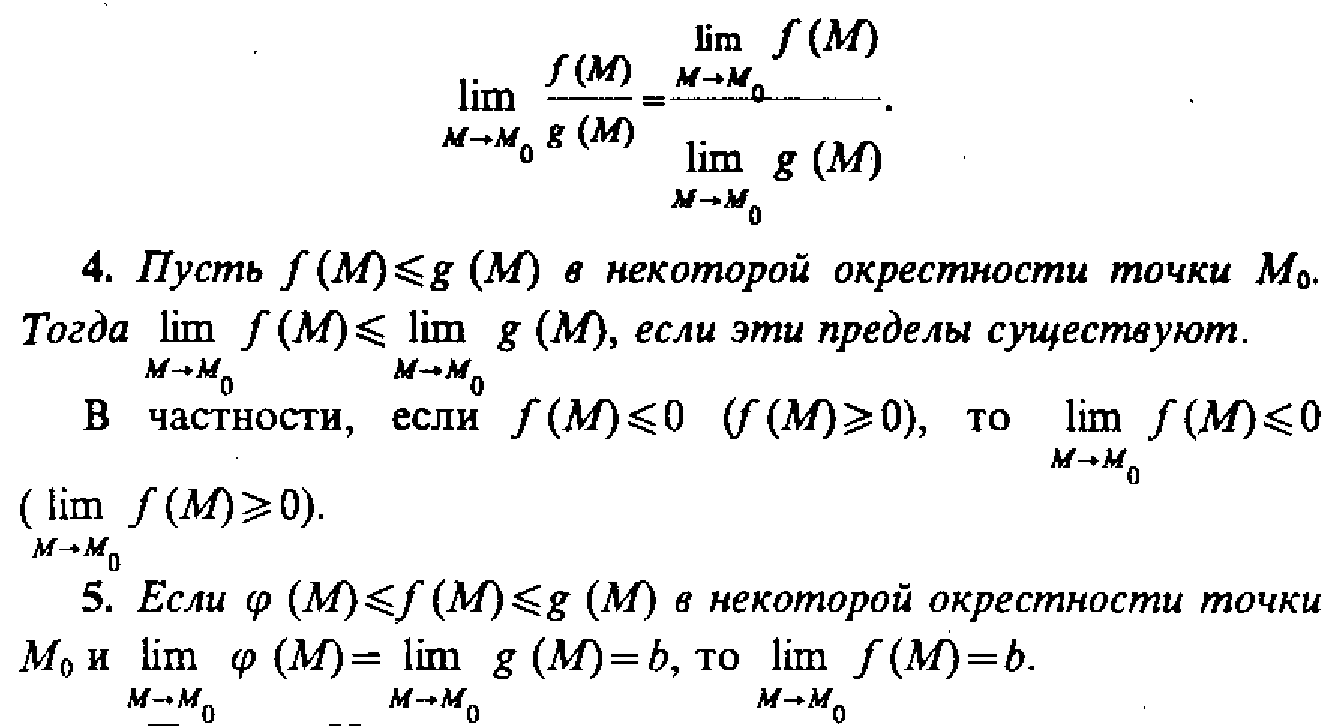
5. Замечательные пределы

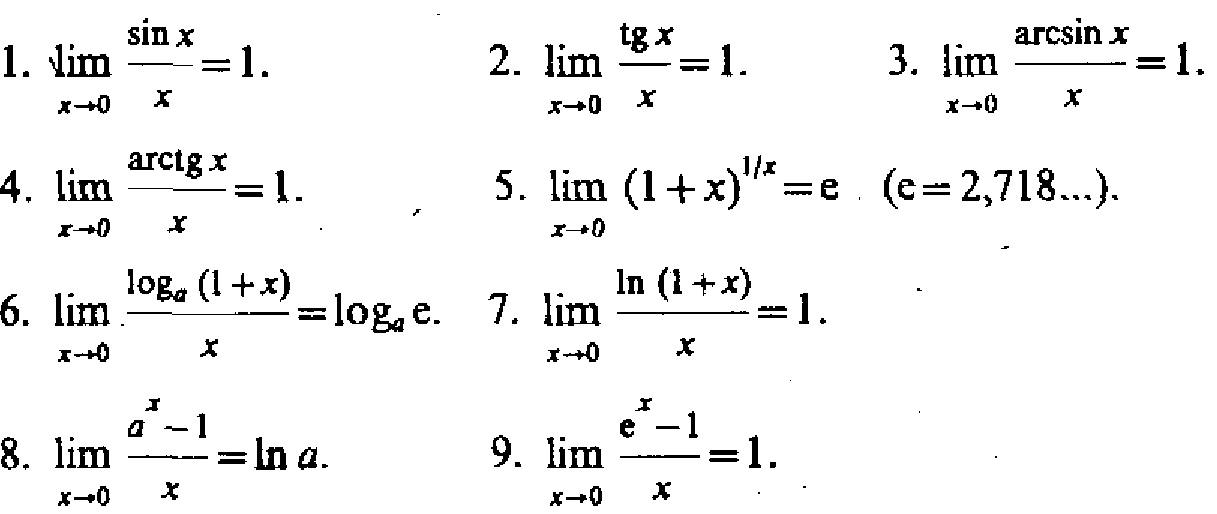
Рассмотрим сектор АОС

S_кр=πr^2=π (т.к r =1)→2π радиан, S_сек=у →х радиан

У=S_сек=πх/2π=х/2

S_АOC<S_секАОС<S_BOC

1/2*1*sinx≤x/2≤1/2*1*1*tgx

(*)1<x/sinx<1/cosx,х є (0;2π) х=-у след-но у є (-π/2;0) 1<-y/sin(-y) < 1/cos(-y) 1<y/siny<1/cosy y є(-π/2; 0)

Отсюда с учетом нер-ва(*) получаем (**) 1<x/sinx<1/cosx,х є (-π/2;0)υ(0;π/2). Т.к 1/cosx стремится к 1/cosx=1,то из нер-ва(**) по теореме о пределе пром ф-ии lim_x→0 x/sinx=1

5. Понятие о производной.Механич. и геометрич.смыслы

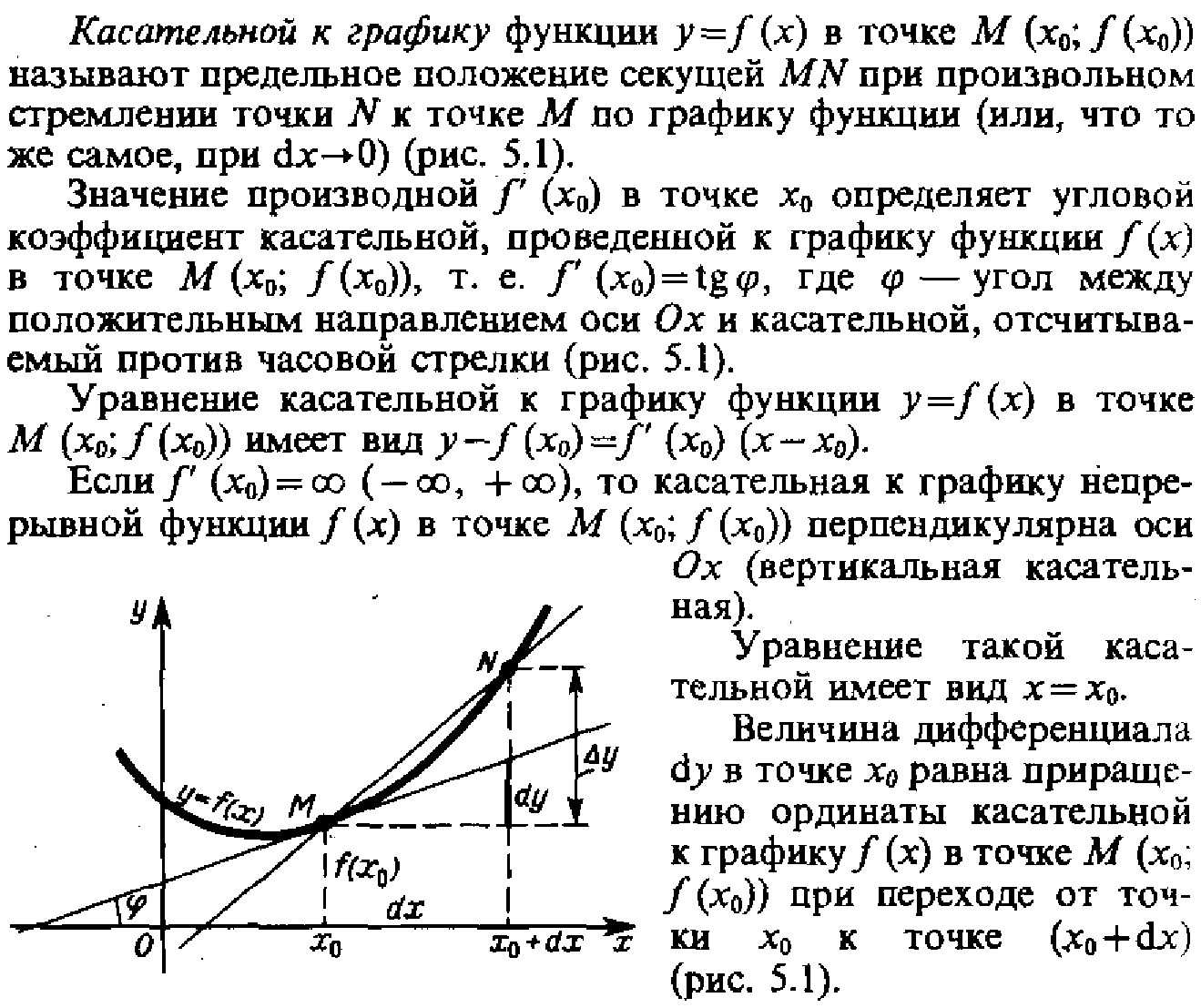
5. Теоремы о произв.пост.величины,суммы, произвед,дроби

(10,11,12,13,14,15,16,17)

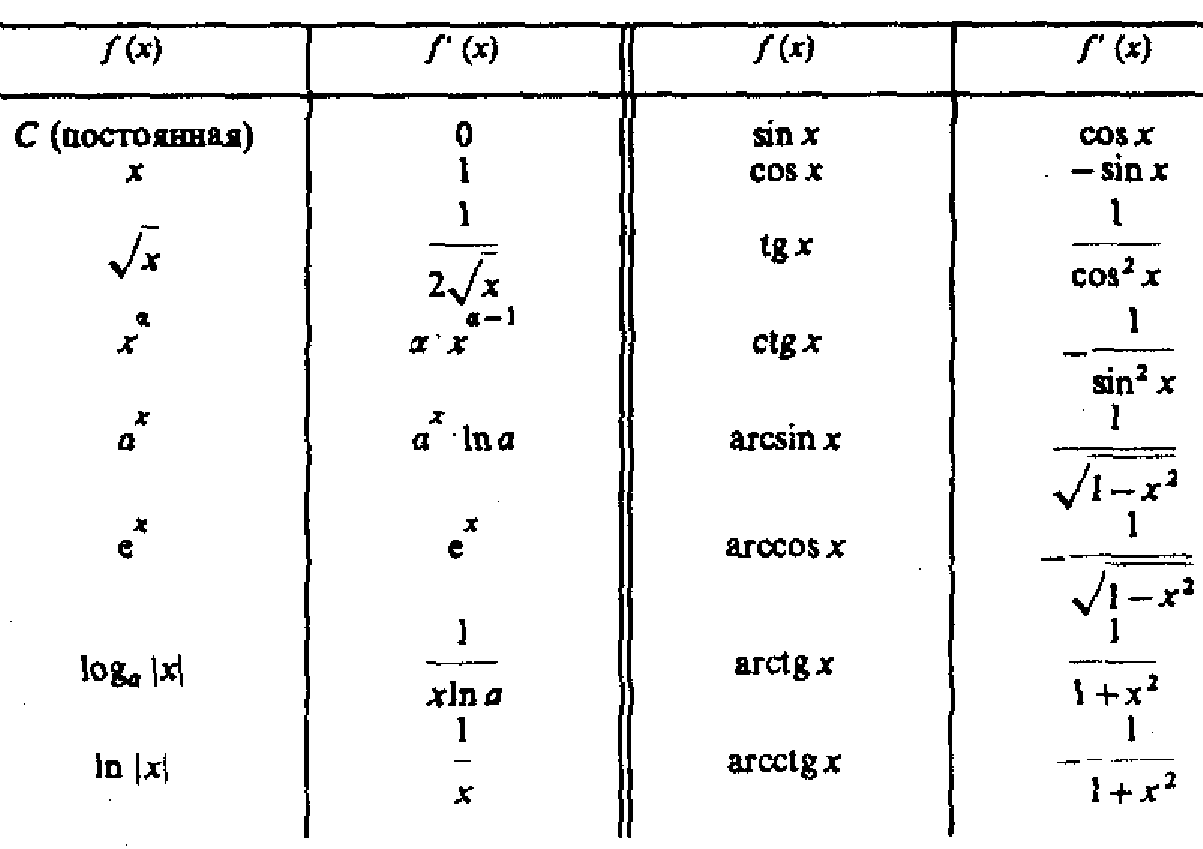
18. Производные высших порядков ф-ций с одной переменной

19. Теорема о корнях производных(Ролля)

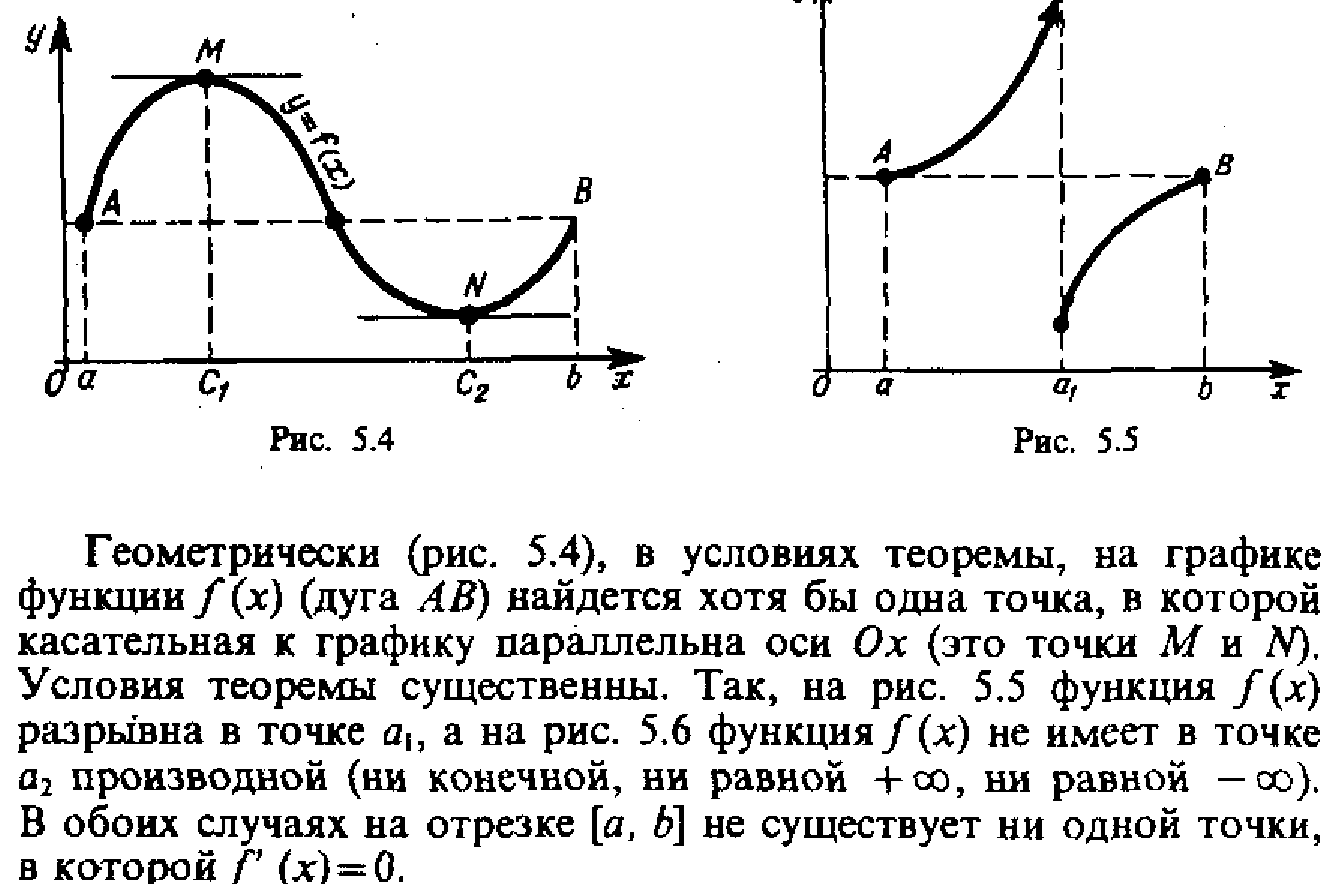
20. Теорема о конечном приращении ф-ции(Лагранжа)

21 Правило Лопиталя

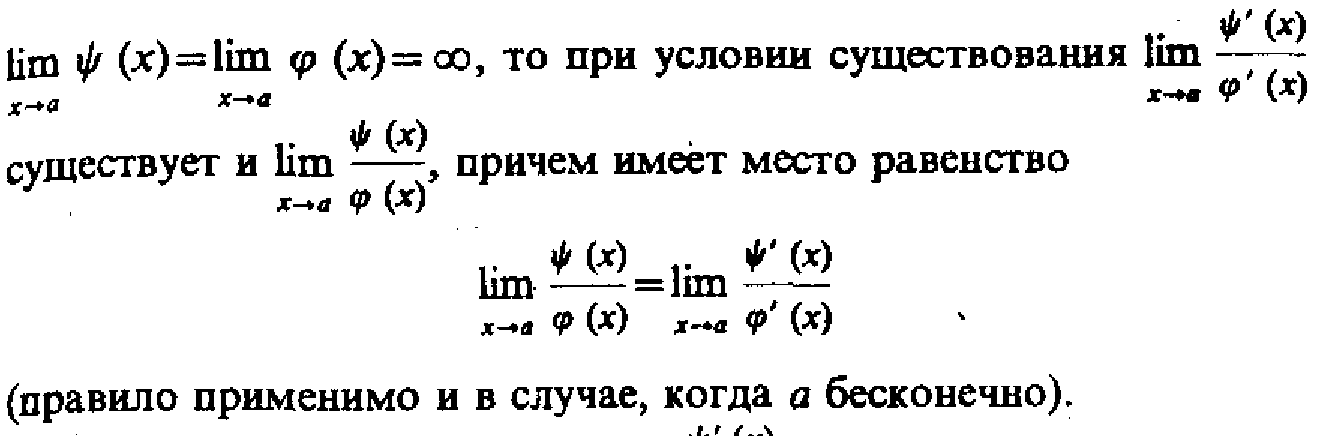
22. max и min ф-ций

23. Необходимое условие существования экстремума ф-ции с одной перем.

24. Достаточное условие существования экстремума ф-ции с одной перем.

25. Асимптоты

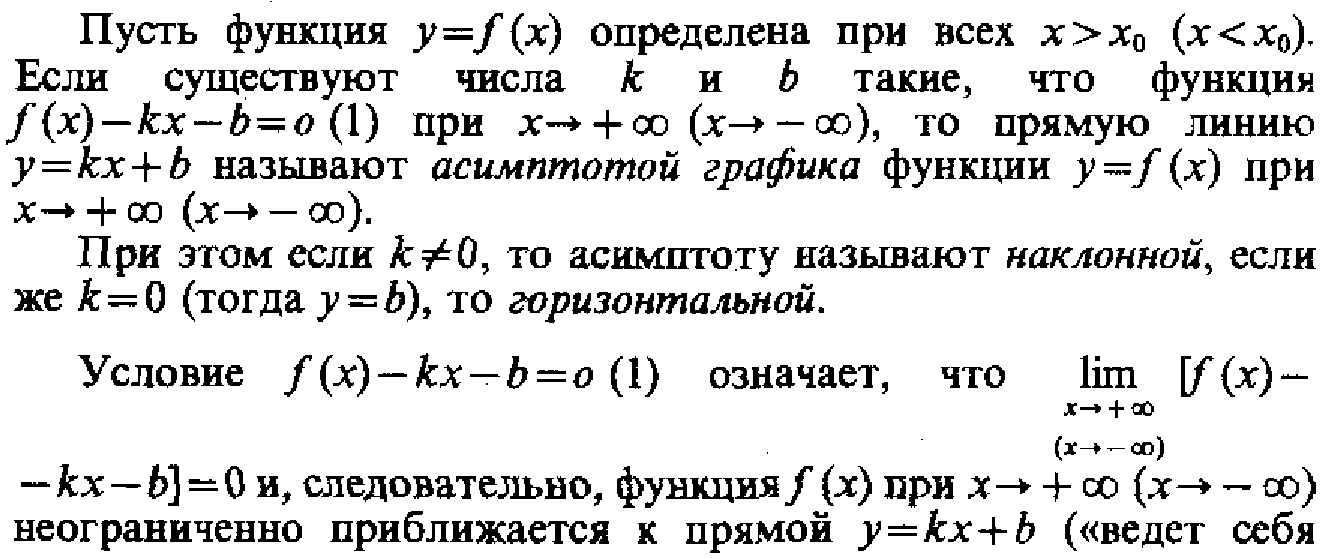
26. Дифференциал ф-ции с одной переменной

27. Функции многих переменных. Частные и полные приращения(28)

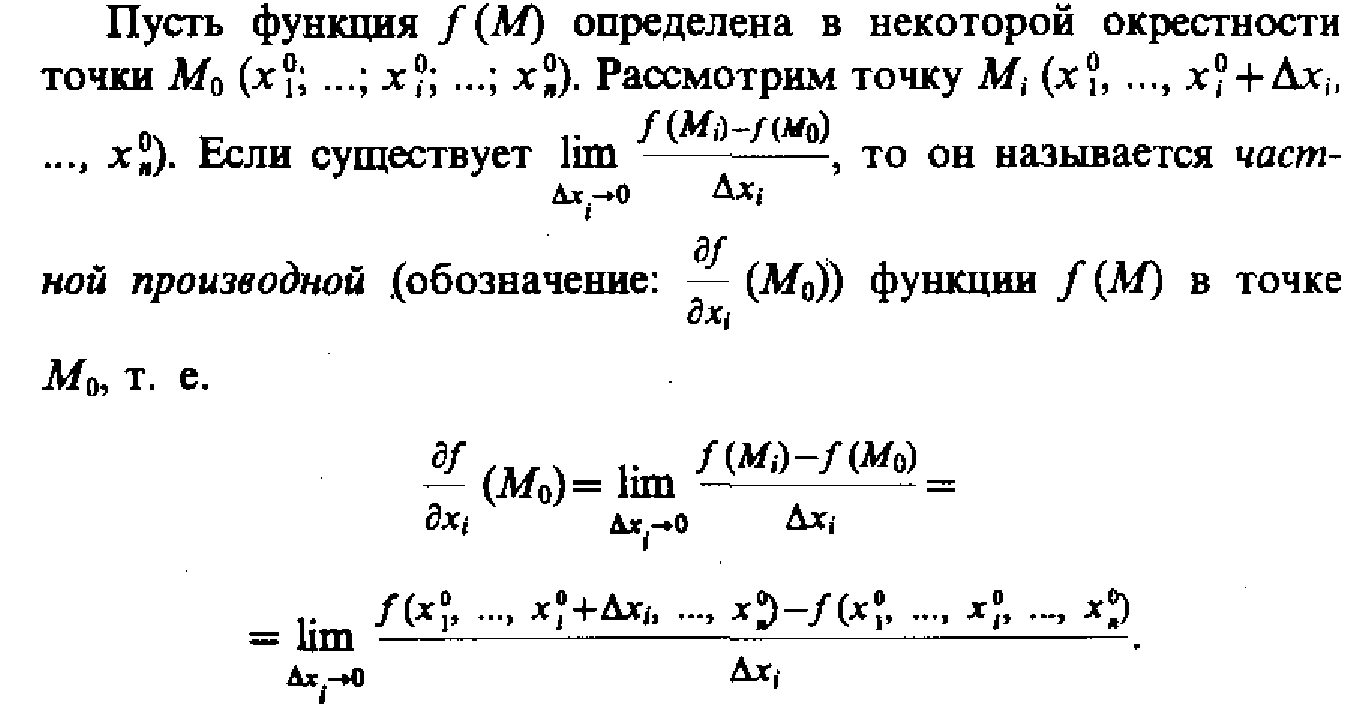
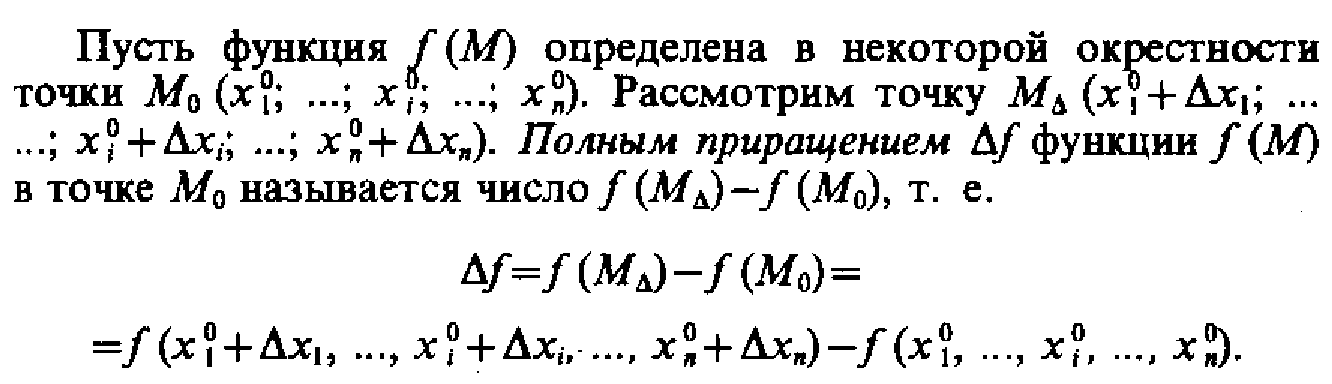
29. Частные производные высших порядков

30. Дифференциал ф-ции многих переменных

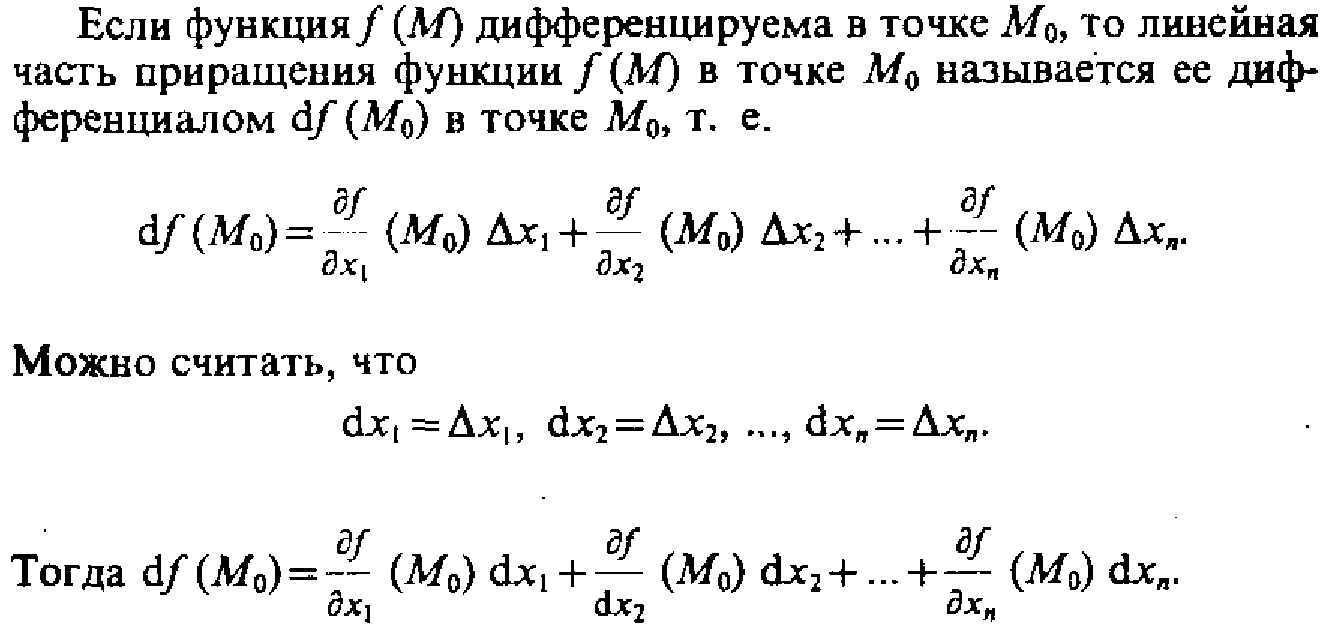
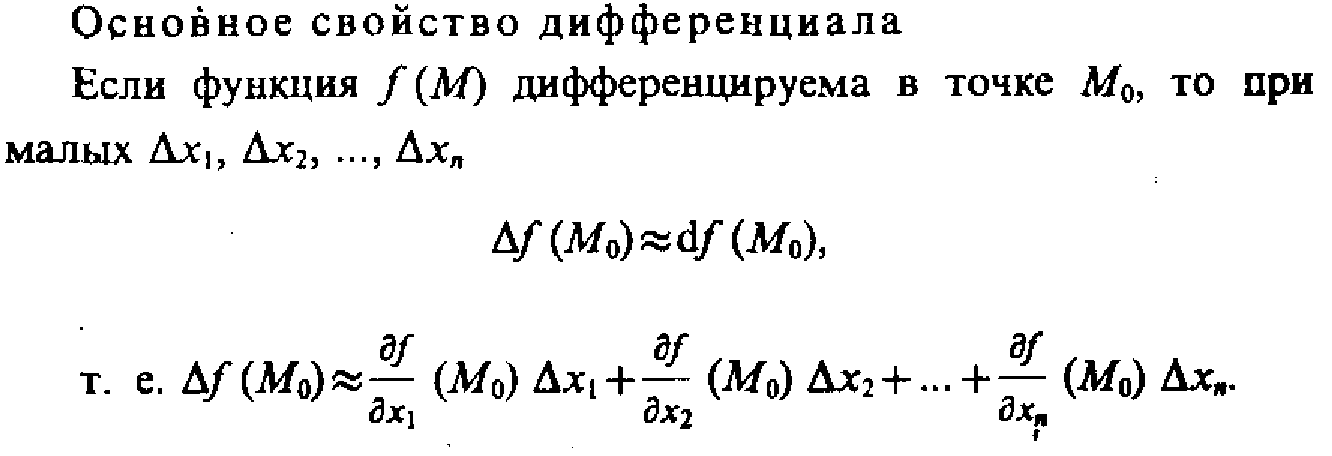
31. Экстремум ф-ции многих перем. Необходимое условие существования

32. Достаточное условие экстремума ф-ции многих переменных

все частные производные равны 0

33.Условный экстремум. Ф-ция Лагранжа

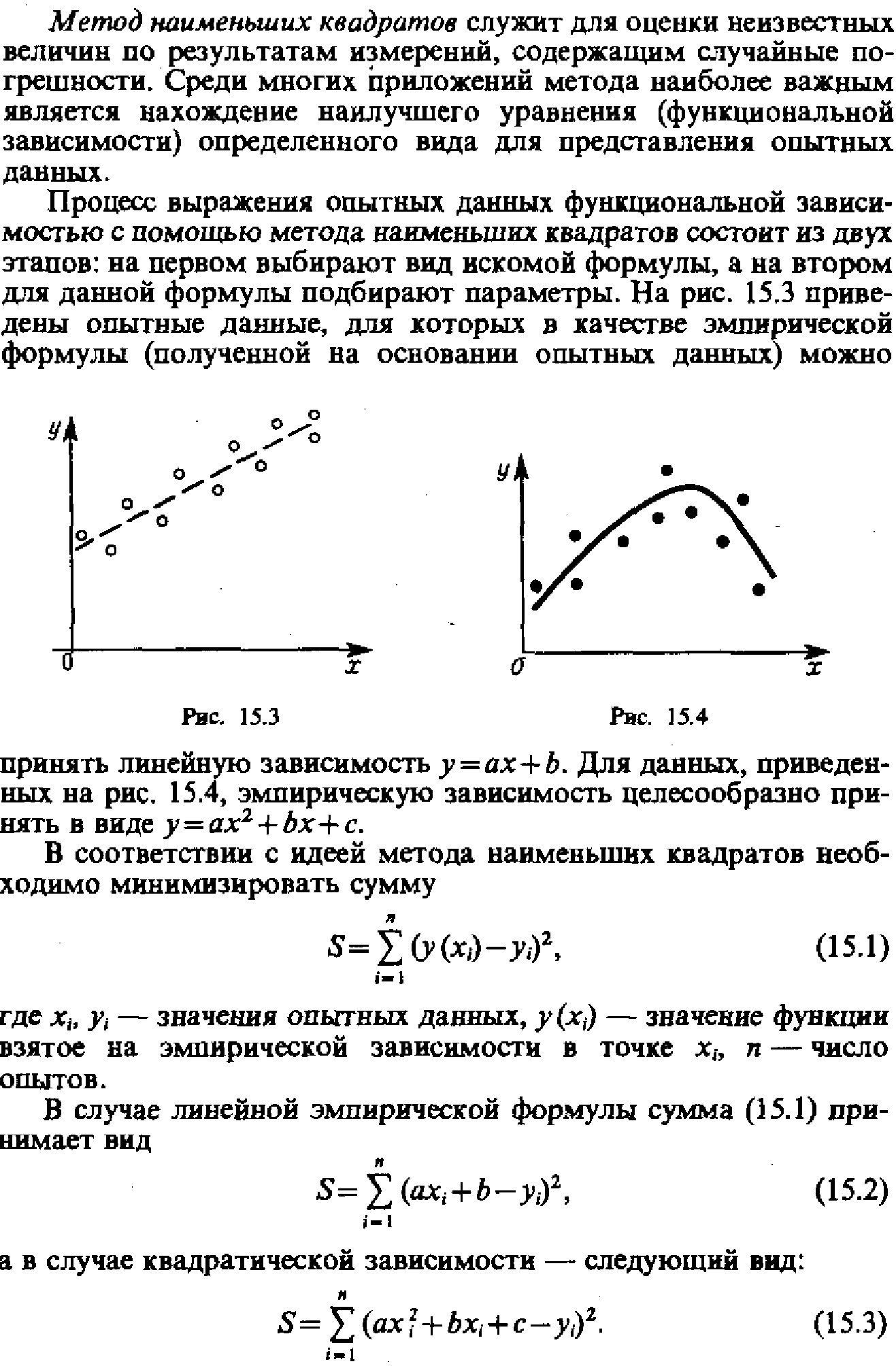
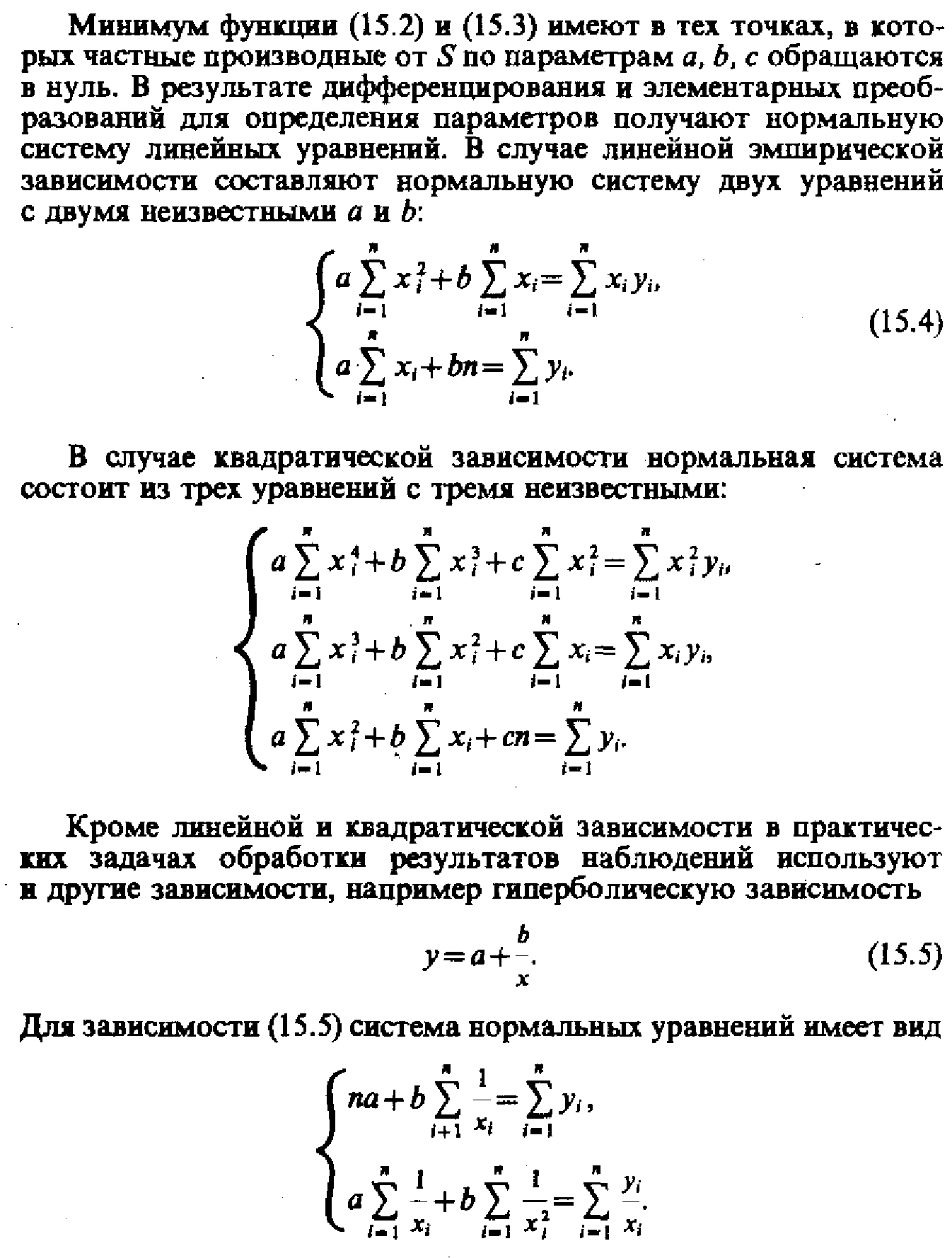
34. Метод наименьших квадратов

35. Первообразная и неопределённый интеграл. Таблица интегралов.

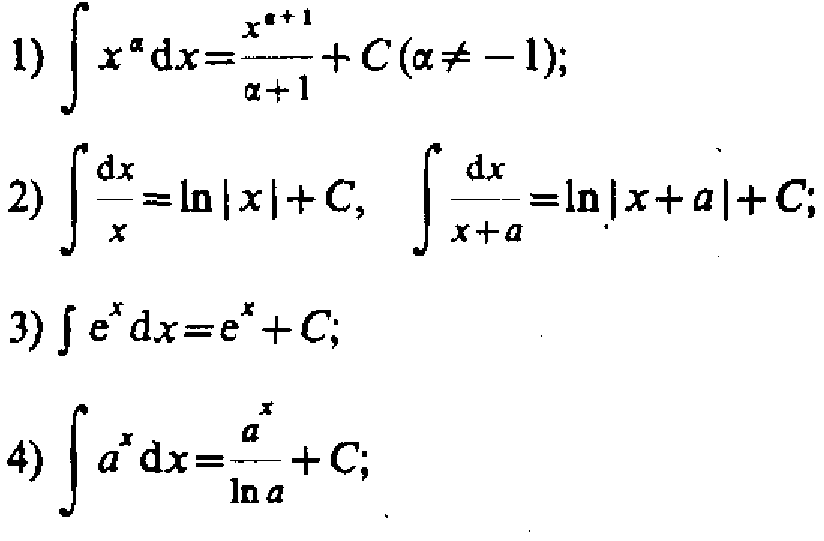
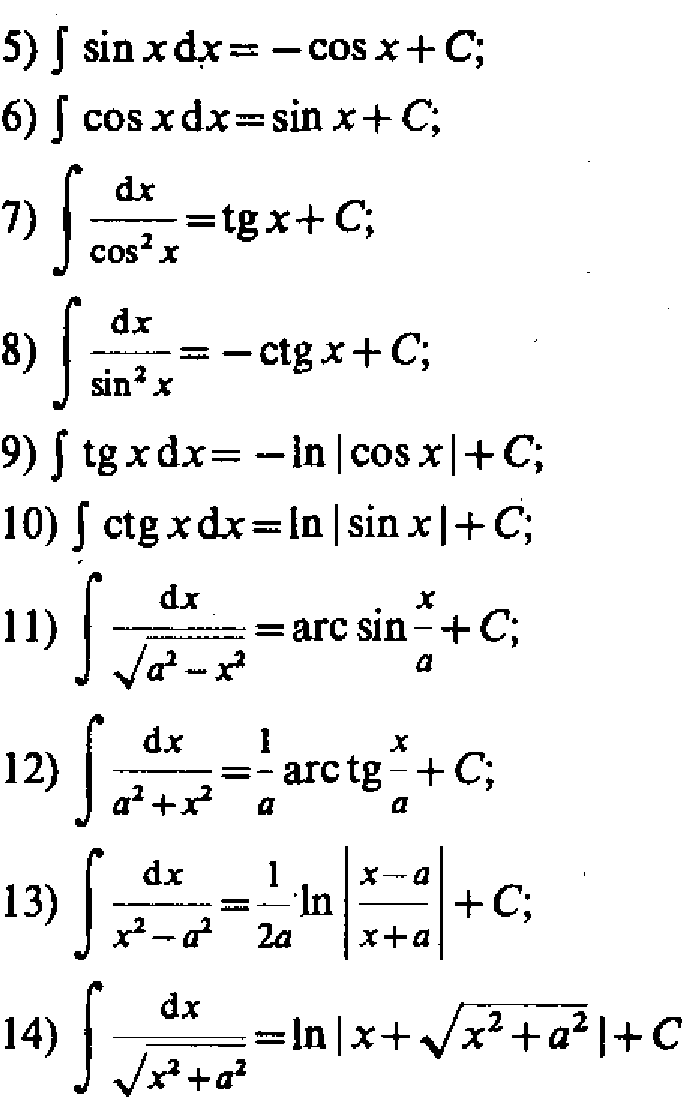
36. Метод замены переменных при интегрировании

37. Интегрирование по частям

38. Интегрирование тригонометрических функций

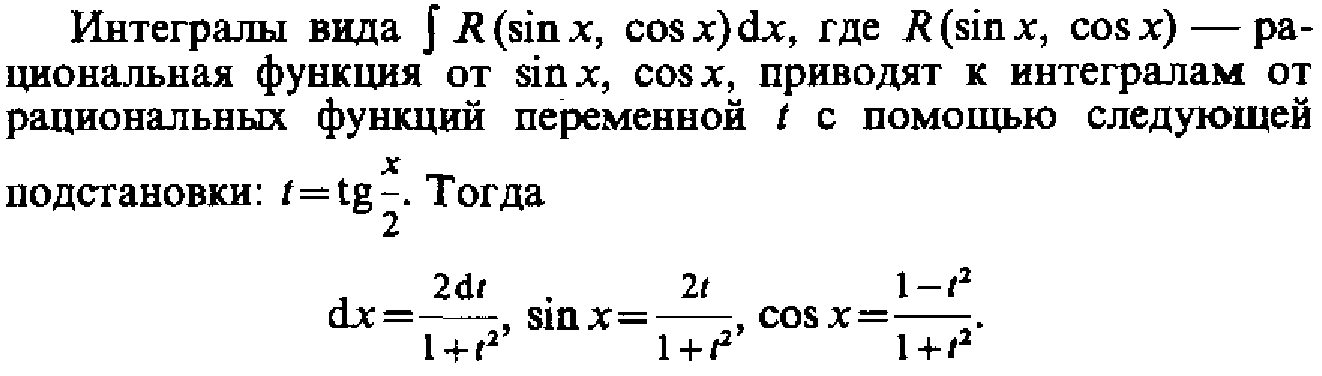
39. Интегрирование рациональных дробей

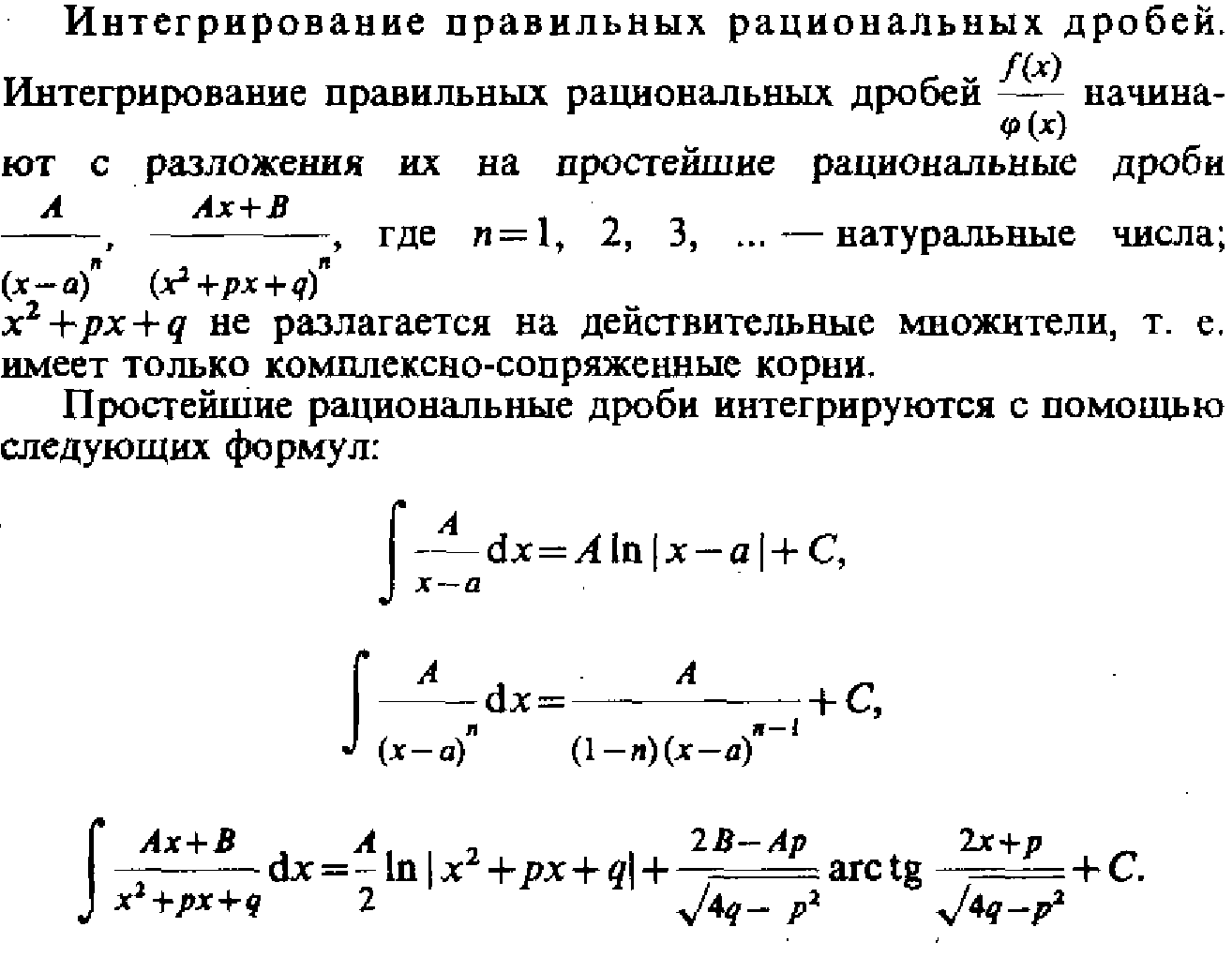
40. Определённый интеграл как предел интегральной суммы. Формула Ньютона-Лейбница.

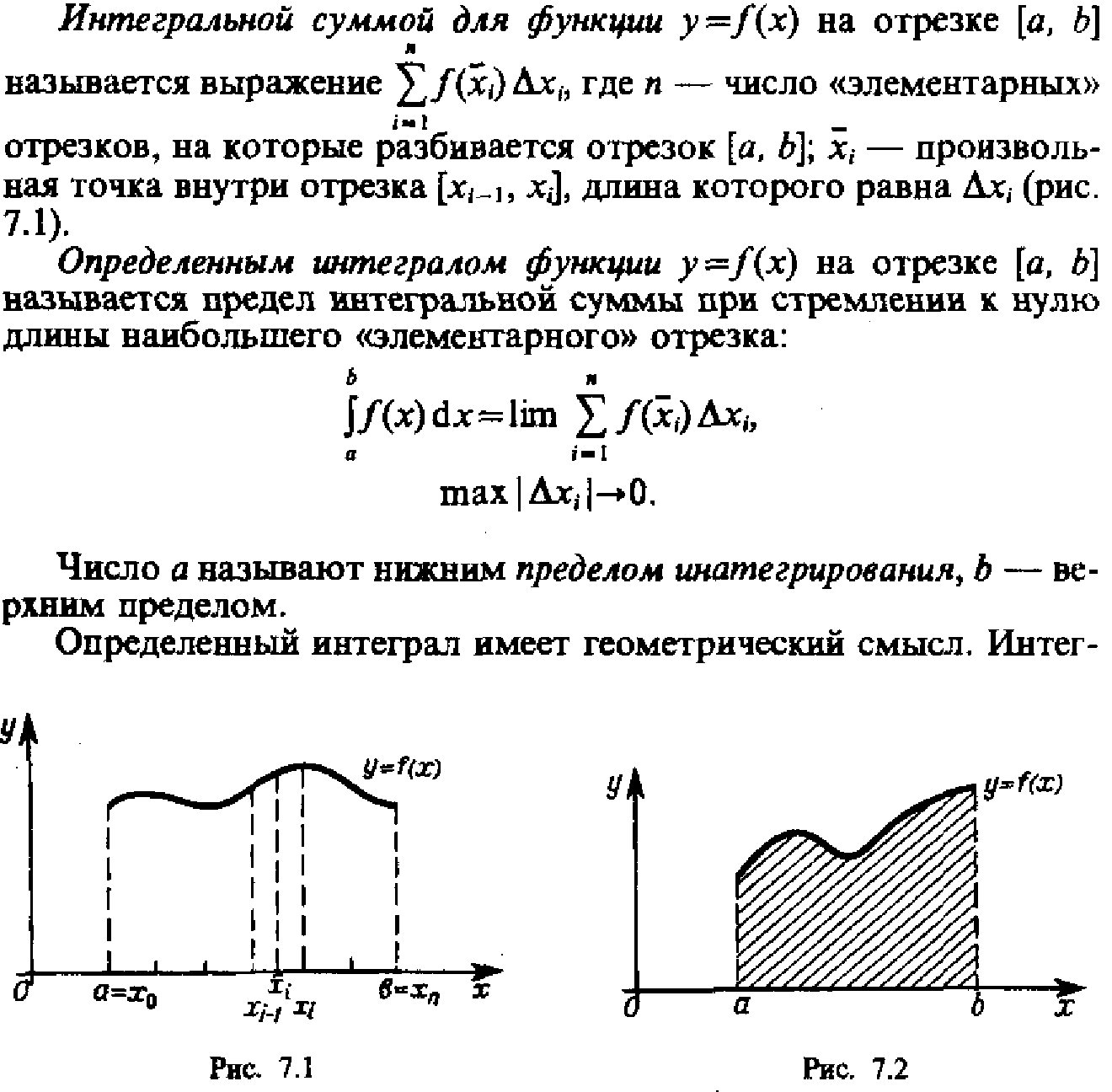
41. Вычисление площадей плоских фигур с пом.опред.интеграла

42. Вычисление объёмов тел вращения

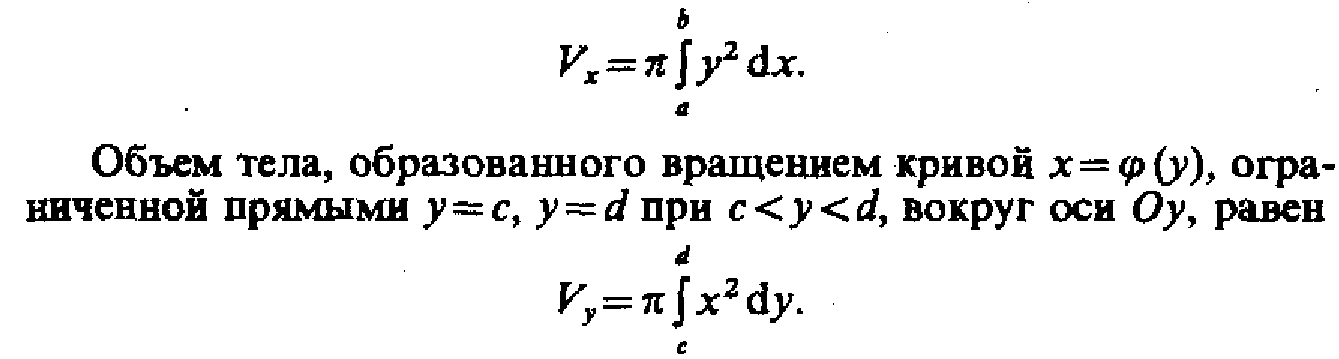
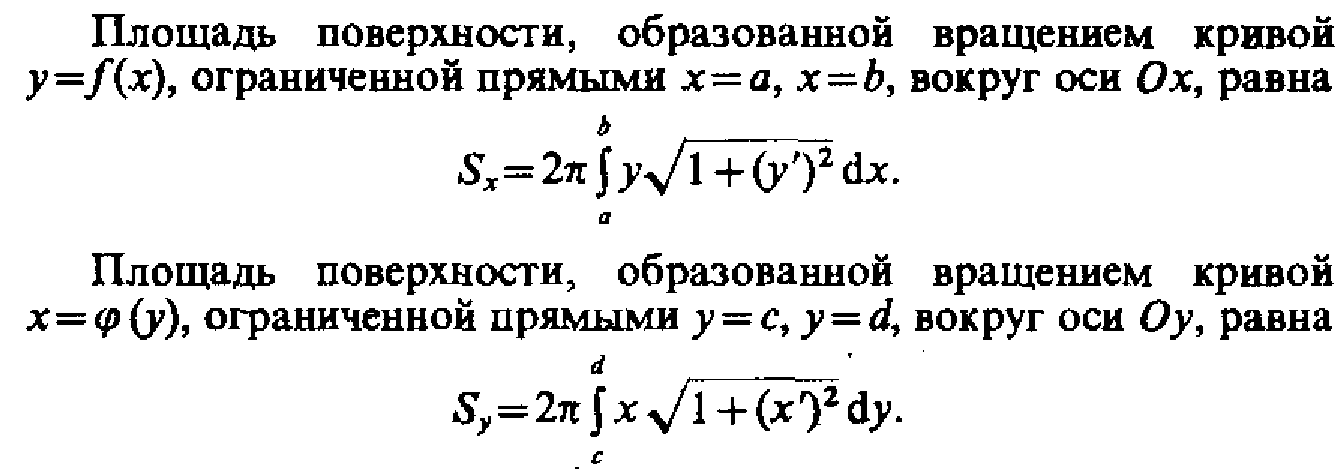
43. Вычисление длины кривой

44. Приближённые методы вычисления определённого интеграла

45. Несобственные интегралы

46. Кратные интегралы

9