2-3

Билет 2.

6 свойств определенного интеграла:

1)Если f(x) интегрируема в наибольшем из промежутков [a,b], [a,c], [c,b], и acb, тогда она интегрируема в двух других и имеет место равенство

каково бы ни было взаимное расположение точек a, b, c.

2)Пусть ф-я f(x) и интегрируемы на отрезке [а,b] и удовлетворяют условию f(x). Тогда

3) Если f(x) интегрируем в промежутке [a,b], то и kf(x) (k=const) также интегрируема в этом промежутке, причем

4) Если f(x) и g(x) – обе интегрируемы в промежутке [a,b], то и f(x) g(x) также интегрируема в этом промежутке, причем

.

5) Если f(x) интегрируема в [a,b], где a<b, и если во всем этом промежутке имеет место неравенство m≤f(x)≤M, то

6)теорема о среднем значении.

Пусть f(x) интегрируема в [a,b] (ab) и пусть во всем этом промежутке m≤f(x)≤M, тогда

где m≤f(c)≤M.

Доказательство:

Если a<b, то по свойству 5 будем иметь откуда

Положив

.Т.к. f(x) непрерывна на [a,b], то по второй теореме Больцано-Коши, она принимает промежуточное значение в не которой точке с отрезка [a,b],т.е. найдется с[a,b],такая, что =f(c),т.е.f(c)= или

2. Площaдь S плоской облaсти G вырaжaется, в зaвисимости от рaссмaтривaемой системы координaт, следующими интегрaлaми:

в декaртовых прямоугольных координaтaх,

в криволинейных координaтaх. Здесь

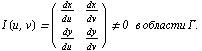
В чaстности, в полярных координaтaх имеем

Конец формы

Двукратный интеграл

Пусть функция f(x,y) непрерывна в обл. D, правильной в направлении оси Оу. Рассмотрим интеграл

Его называют повторным или двукратным интегралом по области D.

При вычислении двукратного интеграла сначала вычисляется внутренний интеграла вычисляется внутренний интеграл

Он вычисляется в предположении, что переменная х сохраняет постоянное значение, а интегрирование проводится по переменной у. В результате получится непрерывная функция только переменной х.

После того, как эта функция Ф(х) определена, вычисляется внешний интеграл

В результате этого вторичного интегрирования получится некоторое число.

Если область Dправильная в направлении оси Ох, то двукратный интеграл по обл. D

Внутренний интеграл вычисляется по переменной х, а переменная у считаетс постоянной величиной, внешний интеграл вычисляется по переменной y.

Расстановка пределов в двукратном интеграле:

1. У внешнего интеграла пределы всегда постоянны.

2. У внутренного интеграла оба предела постоянны только тогда, когда областью интегрирования является прямоугольник. В общем случае пределы внутреннего интеграла есть функции той переменной, по которой вычисляется внешний интеграл и которая при вычислении внутреннего интеграла считается постоянной.

Билет №3

Определенный интеграл с переменным верхним пределом

Пусть функция f(t) интегрируема на отрезке [а,Ь]. Возьмем ∀x∈ [a,b]. По свойству 3° f(t) интегрируема и на отрезке [а, х]. Подсчитаем . Это будет некоторое число, равное площади

криволинейной трапеции аАХх

Таким образом ставится в соответствие число. Тем самым на отрезке [a,b] задана функциякоторую называют определенным интегралом с переменным верхним пределом.

Теорема.

Пусть функция f(t) непрерывна на отрезке [a,b]. Тогда функция F(x) имеет производную в каждой точке , причем

Доказательство.

Дадим аргументу приращение и подсчитаем приращение функции

По свойству 3°

поэтому

По теореме о среднем найдется точка , такая, что

Составим разностное отношение

в силу непрерывности f(x) на [a,b]

Таким образом, мы доказали утверждение, сформулированное в главе I о том, что для непрерывной на отрезке [а,b] функции f(x) всегда существует первообразная; примером ее является определенный интеграл

с переменным верхним пределом

Формула Ньютона-Лейбница

Теорема. Пусть Ф(х)- какая-либо первообразная для непрерывной функции f(x) на отрезке [a,b]

Тогда справедлива формула

Доказательство

Для непрерывной на отрезке [a,b] функции f(x) интеграл является первообразной функцией.

Доказано, что разность между двумя первообразными равна постоянному числу, т. е. F(x)-Ф(x)=C. Чтобы определить С, положим здесь х = а и учтем, что F(a)=0. Тогда 0—Ф(а)=С или С = - Ф(а). При х = b получим F(b) =

Формулу называют формулой Ньютона-Лейбница. Она устанавливает, что значение определенного интеграла равно разности двух значений любой первообразной функции - значению в верхнем пределе интеграла и значению в нижнем пределе интеграла.

§ 5. Тройной интеграл

1.Определение

Пусть в некоторой пространственной области V, ограниченной и замкнутой, задана непрерывная функция f(x,y,z). Разобьем область V на конечное число пространственных ячеек e1,e2,en , имеющих объемы

V(e1),V(e2),…,V(еn). В каждой ячейке ei возьмем произвольно точку Qi(xi,yi,zi). Составим интегральную сумму для функции f(x,y,z) по области V

Если существует конечный , то функция f(x,y,z) называется интегрируемой в области V, а величина предела называется тройным интегралом от функции f(x,y,z) по области V и

обозначается или

2.Вычисление тройного интеграла

Пространственная область V называется правильной, если:

1)прямая, параллельная оси Oz, проведенная через любуювнутреннюю точку области V, пересекает границу области ровно в двух точках;

2)область D - проекция области V на плоскость хОу – правильная двухмерная область.

В общем случае такая область V ограничена сверху поверхностью z = 2(х,у), снизу поверхностью z = 1 (x,y), а с боков - цилиндрической поверхностью с образующими параллельными оси Oz Предположим, что область D ограничена линиями y= 1(x), y=2(x), x=a, x=b

Определение. Трехкратным интегралом по области V от функции f(x,y,z), непрерывной в области V называется

интеграл

Сначала вычисляется внутренний интеграл , при этом

переменные х и у рассматриваются как постоянные, а интегрирование проводится по переменной z в пределах от значения z на нижней границе области V до значения z на верхней границе области V. В результате получается функция F(x,y) двух переменных х и у. Затем вычисляется двойной интеграл

Теорема. Тройной интеграл от функции f(x,y,z) по правильной области V равен трехкратному интегралу от f(x,y,z) по области V (без доказательства).

Замена переменных в тройном интеграле. Цилиндрические и сферические координаты

Пусть функции

х = (u,t,w),

y = (u,t,w)

z= χ (u,t,w)

задают регулярное отображение пространственной области V в декартовых координатах х, у, z на области V в криволинейных координатах u, t, w.

Аналогично тому, как это было сделано для двойного интеграла, можно доказать, что формула замены переменных в тройном интеграле имеет вид , где I-якобиан отображения

Наиболее употребительные системы криволинейных координат в пространстве - цилиндрические и сферические координаты.

В цилиндрических координатах положение точки М в пространстве определяется ее декартовой координатой z и полярными координатами р, <р ее проекции Мху на плоскость хОу. Из рисунка видно, что цилиндрические координаты точки М связаны с ее декартовыми следующими соотношениями:

x = p*cosq,

y=p*sin𝛗

z=z

Якобиан, соответствующий переходу от декартовых координат к цилиндрическим равен

Тройной интеграл от функции f(x,y,z) в прямоугольных координатах преобразуется в тройной интеграл в цилиндрических координатах по формуле