19

Билет № 19.

1. Интегрирование по частям.

   0. Для неопределенных интегралов.

Для неопределенных интегралов.

Пусть u(x) и V(x) дифференцируемые функции. По правилу дифференцирования произведения двух функций d(uV)= udV+Vdu или udV = d(uV) – V(du). Возьмем интегралы от обеих частей этого равенства (1)

Формула (1) называется формулой интегрирования по частям. Для применения этой формулы нужно подынтегральное выражение представить как произведение двух множителей u и dV так, чтобы задача вычисления двух интегралов – V(x) = $dV b $du – была бы легче, чем вычисления исходного интеграла. Если подынтегральное выражение есть произведение алгебраического многочлена на какую-либо тригонометрическую или показательную функцию, то за u надо брать многочлен, а все остальное за dV.

Если под интегралом есть логарифмическая функция или обратная тригонометрическая, то за u нужно брать логарифмическую функция или обратную тригонометрическую, все остальное за dV/

1.2 Для определенных интегралов.Пусть функции u(x) и V(x) имеют непрерывные производные на отрезке [a,b]. Тогда (2)

Доказательство. Обозначим . По формуле Ньютона-Лейбница получаем

Так как , то приходим к формуле (2).

2.Ряд Тейлора.

Пусть функция f(x) определена в окрестности точки a и в точке x=a имеет производные до n-ого порядка включительно. Тогда для любого значение f(x) можно приближенно найти по формуле Тейлора

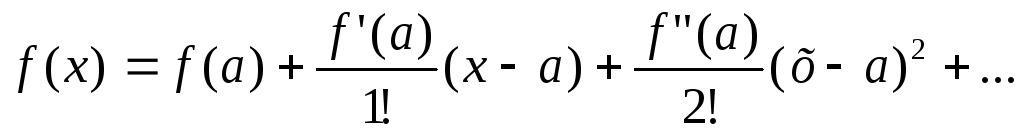
Точность приближения характеризуется значением остаточного члена Если в u(a) функция f(x) имеет производную (n+1)-го порядка, то остаточный член может быть представлен в форме Лагранжа.

, a<c<x

Пусть функция f(x) определена в u(a) и имеет производные любого порядка в точке x=a, т.е. .Тогда в формуле Тейлора мы можем брать n сколь угодно большим и записывать справа бесконечное число членов. Таким образом, мы приходим к следующему ряду:

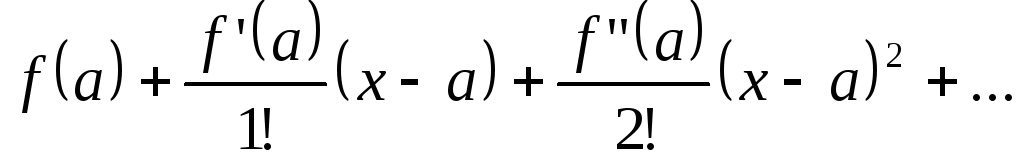
Этот ряд независимо от того, сходится ли он и имеет ли своей суммой f(x), называется рядом Тейлора функции f(x) по степеням (x-a). Ряд Тейлора есть степенной ряд вида

коэффициенты которого an есть коэффициенты многочлена Тейлора

В частности, при a=0 получим ряд Тейлора по степеням x. Его называют рядом Маклорена.

Теорема1.Если функция f(x) разлагается в степенной ряд на итервале (-R, R), то этот ряд является ее рядом Телора, т.е. его коэфф. Находятся по формулам Тейлора

Доказательство.Пусть

По свойству 5 для степенных рядов сумма ряда f(x) ,бесконечно дифференцируема и имеют место равенства

……………………………………………………………………………………...

Полагая в этих равенствах x=0, получим

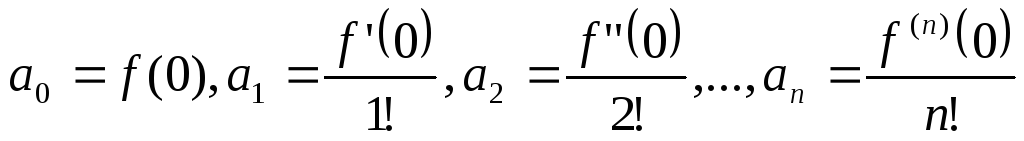
Мы доказали, что если функцию f(x) можно разложить в степенной ряд, то он является для этой функции рядом Тейлора.

Следствие. Если функция f(x) разлагается в степенной ряд на интервале (-R,R), то это разложение единственно. Допустим противное: сущ. два разложения:

По теореме 1 оба ряда есть ряды Тейлора для f(x). Следовательно их коэф. совпадают:

Замечание.Существуют функции, ряд Тейлора которых сходится, но не к данной функции. Проведем пример такой функции.

Функция в точке x=0 имеет производные любого порядка, равные нулю.Поэтому коэф.Тейлора для это йфункции равны нулю. Ряд Тейлора сходится и его сумма S(x)=0, но функция f(x)=0 только при x=0.

Теорема 2. Для того, чтобы функцию f(x) можно было разложить в степенной ряд на интревале (-R,R), R0, необходимо и достаточно, чтобы f(x) имела на этом интервале производные всех порядков и чтобы остаточный член в форм.Тейлора

стремился к нулю при при всех .

Доказательство.1.Пусть f(x) = (-R,R), тогда по св-ву 5 для степенных рядов f(x) имеет производные всех порядков внутри (-R,R). По теореме 1 ряд f(x) = (-R,R) есть ряд Тейлора ф-ции f(x) и данное рав-во можно переписать как 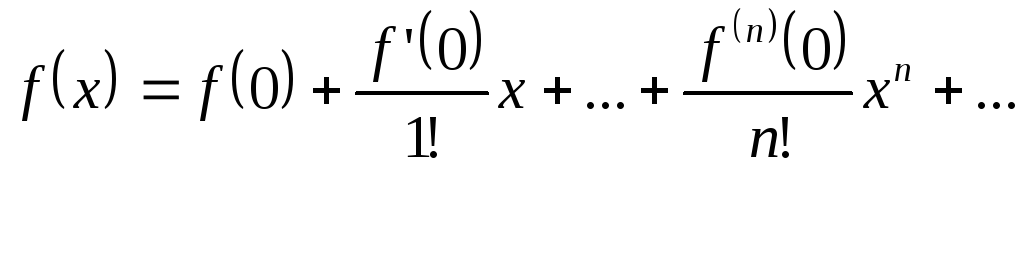так как этот ряд сходится на (-R,R) то для всех (-R,R) разность между суммой и частной суммой ряда, равная остаточному члену в ф.Тейлора, т.е. при для всех (-R,R).

2.Пусть f (x) имеет производные всех порядков на интервале (-R,R) и остаточный член в ф-ле Тейлора при для всех (-R,R). Так как остаток ряда , то ряд сходится и его сумма равна f(x) на инт. (-R,R).

Теорема 3. Для того, чтобы функцию f(x) можно было разложить в степенной ряд на интревале (-R,R), R0, необходимо и достаточно, чтобы f(x) имела на этом интервале производные всех порядков и чтобы все эти производные были равномерно ограничены на интервале (-R,R).

Доказательство. По усл-ю производные всех порядков ограничены на (-R,R). Это означает, что существует такое число M, что при n=0,1,2,…и всех (-R,R) (*)

Так как ф-ция f(x) имеет произв. всех порядков на (-R,R), то для нее можно построить ряд Тейлора. Чтобы док-ть, что этот ряд сходится к f(x), достаточно, согласно теореме 2, док-ть, что остатю член в ф-ле Тейлора стермится к нулю при при всех (-R,R). Записав остаточный член в форме Лагранжа, получим в силу (*), следующую оценку:

< при n=1,2…и (-R,R) (**)

0<с<1. По признаку Даламбера можно установить что ряд сходится, поэтому и

При и всех (-R,R) в силу (**)