Уравнение Рейнольдса 17-3

(17) Уравнение Рейнольдса для турбулентных потоков.

Дифференциальные уравнения движения реальной жидкости при турбулентном режиме – уравнения Рейнольдса

Можно предположить, что как при ламинарном, так и при турбулентном движении справедливы закон внутреннего трения Ньютона ,

а значит и опирающиеся на него уравнения Навье-Стокса

(и т.д. по осям и )

Однако использовать уравнения Навье-Стокса для турбулентного режима движения практически невозможно, так как входящие в них мгновенные скорости и давления являются пульсирующими величинами. Поэтому для турбулентного режима ставится задача отыскания осредненных во времени скоростей и давлений.

Для получения уравнений Рейнольдса используются уравнения Навье-Стокса, все члены которых подвергаются операции осреднения.

Операция осреднения основана на предположении о существовании для данного турбулентного движения такого интервала осреднения Т, что выполненное по нему осреднение не изменяется при повторном осреднении.

Операция осреднения производится по определенным правилам.

Пусть и суть зависимые переменные, которые необходимо осреднить, и пусть – есть одна из независимых переменных ( ).

Правила осреднения

1. прим.: повторное осреднение осредненной есть сама осредненная

2. : осредненная сумма есть сумма осредненных

3. : осреднение произведения осредненной на неосредненную есть произведение осредненных

4. : осреднение производной есть производная осредненной

5. : осреднение интеграла есть интеграл осредненной

Запишем первое из уравнений Навье-Стокса*¹ (остальные преобразуются аналогично)

_(*)

Движение установившееся, значит локальная производная скорости в правой части уравнения равна нулю .

Конвективную часть производной преобразуем.

Предварительное замечание. Рассмотрим сумму производных произведений*² скоростей и приведем ее к виду правой части имеющегося уравнения.

Уравнение неразрывности в дифференциальной форме

С учетом приведенных замечаний получим

Выполнив операции осреднения членов уравнения получим

_(*)

Вспомним, что мгновенная скорость представляется суммой осредненной и пульсационной составляющей , и . Осредненная пульсационная составляющая равна нулю

При дальнейших преобразованиях учтем, что

Произведем преобразование*³ правой части полученного выше уравнения

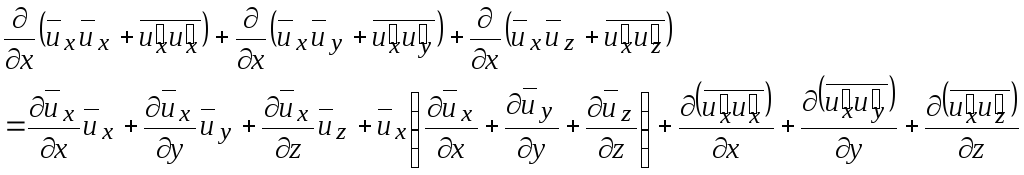После осреднения уравнение неразрывности , значит скобка при в правой части равна нулю.

_(*)

Каждый из членов, содержащих пульсационные составляющие скорости, можно переписать в ином виде:

Уравнения Рейнольдса:

_(*)

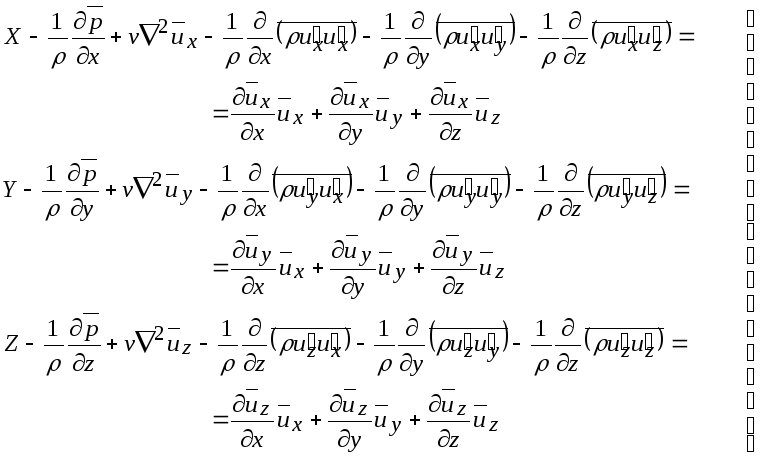Члены вида имеют размерность напряжений. Таким образом в левой части уравнений имеются члены, отражающие действие только вязкостных напряжений и содержащие напряжения, связанные с пульсациями скоростей, т.е. появляющиеся только при турбулентном режиме движения .

При турбулентном режиме касательные напряжения могут быть представлены суммой вязкостных и касательных напряжений, появляющихся вследствие турбулентных пульсаций :

.

Турбулентные касательные напряжения выражаются формулой , при этом они подчиняются свойству взаимности .

Полученная система является незамкнутой.

Проблема замыкания уравнений Рейнольдса в общем виде не решена.

Конец раздела 17

1* Напомним физический смысл членов уравнения. Проекция на ось х плотности распределения массовых сил. Распределение гидродинамического давления. Влияние вязкости жидкости. Правая часть – полная производная, состоящая из локальной (первое слагаемое) и конвективной (три слагаемых) частей.

2* Производная произведения есть производная первого сомножителя, умноженная на второй плюс производная второго сомножителя, умноженная на первый

3* производная суммы есть сумма производных