Уравнение Навье-Стокса 09-5

(09) Дифференциальные уравнения движения вязкой жидкости Навье-Стокса.

Общая интегральная форма уравнений количества движения и момента количества движения.

Дифференциальные уравнения движения вязкой жидкости Навье-Стокса

Штеренлихт, стр. 90-97

Напряжения в движущейся вязкой жидкости

В невязкой жидкости действуют только нормальные напряжения.

При движении вязкой жидкости в ней возникают не только нормальные, но и касательные напряжения, так как вязкая жидкость обладает способностью оказывать сопротивление относительному сдвигу своих слоев.

Эти напряжения зависят не только от координат точки, но и от ориентации площадки действия.

Рассмотрим элементарный параллелепипед с ребрами , выделенный в движущейся жидкости.

Обозначим сопротивления на гранях. Первый индекс – направление оси, к которой перпендикулярна данная грань. Второй индекс – направление действия напряжения. Считая напряжение непрерывными, используя разложение в ряд Тейлора, определим напряжения на гранях, удаленных от начала координат. На рисунке показаны только напряжения, действующие на левую и правую грани.

грань	нормальное напряжение	касательное напряжение
левая
правая
задняя
передняя
нижняя
верхняя

Отметим без доказательства, что касательные напряжения на взаимно перпендикулярных площадках, направленные по нормали к линии пересечения этих площадок, равны друг другу:

, ,

Составим уравнение движения массы жидкости, заключенной в элементарном параллелепипеде. Сумма сил, действующих на жидкую частицу, равна произведению ее массы на ускорение. Силы массовые и поверхностные. Сначала в проекции на ось .

Проекция суммарной массовой силы на ось есть произведение плотности распределения равнодействующей массовых сил на массу частицы .

Поверхностные силы действуют на все шесть граней. Они равны произведению соответствующего напряжение (нормального или касательного) на площадь грани. Запишем только силы, проекция которых на ось не равна нулю:

Левая грань и правая:

Задняя грань и передняя:

Нижняя грань и верхняя:

Масса на ускорение:

После сокращения и деления на массу получим

Без доказательства укажем: В вязкой жидкости сумма нормальных напряжений по трем взаимно перпендикулярным граням не зависит от ориентации этих площадок. Введем понятие давления в движущейся жидкости, численно равное среднему нормальному напряжению

Выразим нормальные напряжения на грань через давление и добавочное вязкое напряжение

.

По закону Ньютона, распространяя его на пространственное движение, вязкое напряжение пропорционально

Произведем необходимые подстановки. Упростим, используя уравнение неразрывности в дифференциальной форме .

Учтем, что и по аналогии запишем проекции на другие оси.

Уравнения Навье-Стокса для неустановившегося движения несжимаемой вязкой жидкости

Упростим запись, используя оператор Лапласа ¹

Субстанциальное ускорение в правой части можно раскрыть как сумму локального и конвективного ( аналогично по другим осям).

Эти уравнения совместно с уравнением неразрывности и уравнением состояния образуют замкнутую систему, которая, однако, не имеет общих решений.

Общая интегральная форма уравнения количества движения

и момента количества движения

В основу гидродинамики как раздела гидромеханики положены четыре основных закона механики:

• закон сохранения массы

• закон изменения количества движения (импульса)

• закон изменения момента количества движения

• закон изменения кинетической энергии

Эти законы формулируются для объемов жидкости конечных размеров.

Закон сохранения массы. При движении жидкого объема его масса остается неизменной. . Из этого вытекают уравнения неразрывности в дифференциальной форме и для потока жидкости.

Закон изменения количества движения. Изменение количества движения жидкого объема за единицу времени равно сумме всех приложенных к нему внешних (массовых и поверхностных) сил.

В векторной форме или

Закон изменения момента количества движения. Изменение момента количества движения жидкого объема относительно некоторой неподвижной точки за единицу времени равно сумме моментов всех внешних (массовых и поверхностных) сил, действующих на этот объем.

Закон изменения кинетической энергии. Изменение кинетической энергии жидкого объема за единицу времени равно мощности всех внешних и внутренних (поверхностных и массовых) сил, действующих на этот объем жидкости.

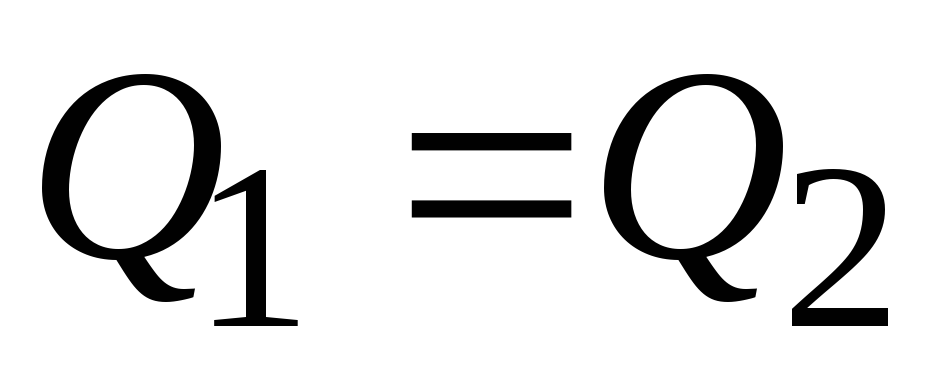
Рассмотрим закон изменения количества движения применительно к потоку жидкости. Жидкость несжимаема : Движение установившееся : На выделенный объем действуют массовая сила веса, поверхностные силы давления , 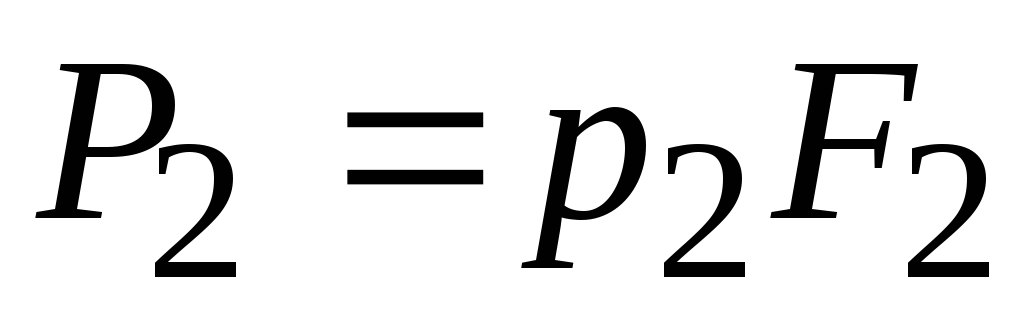и реакция стенок канала . За время жидкость из сечения 1 переместится в сечение 1`, а из сечения 2 в сечение 2`.

Изменение количества движения

Изменение количества движения равно разности количества движения вышедшей массы и вошедшей массы.

Входящая масса

Выходящая масса

Изменение количества движения за единицу времени:

Закон изменения количества движения

( При изображении многоугольника сил (см. рисунок) следует правильно выбирать их направления. Вес вниз, силы давления нормальны к сечениям и действуют внутрь объема,

следовательно , а направления векторов количества движения совпадают с направлениями скоростей, сила реакции обеспечивает поворот).

Как правило неизвестной является реакция стенок канала . Векторное уравнение решается обычно через проекции на оси координат.

1 Дифференциальная операция второго порядка : расхождение потенциального вектора .