
- •А.В. Алёшкин
- •Топологическая матрица
- •Матрица индексов
- •Измененные с троки матрицы жесткости при наложении граничных условий
- •4. Формирование матриц жесткости и масс в глобальной системе координат для рамы
- •Координатная матрица узлов рамы
- •Топологическая матрица элементов рамы
- •Матрица индексов перемещений узлов рамы
- •6. Задания для выполнения лабораторных работ
- •6.1 Исследование вращения твердого тела вокруг неподвижной оси
- •6.2Исследование равновесия твердого тела
- •6.3 Расчет плоской фермы методом конечных элементов
- •Вариант 2
- •6.5 Расчет плоского потенциального течения жидкости методом конечных элементов
- •Литература
6.2Исследование равновесия твердого тела
Определить реакции опор твердого тела под действием заданных активных сил. При нахождении неизвестных сил сотавить уравнения равновесия и представить их в матричной форме. Решить систему линейных уравнений с помощью алгоритмической программы. Выполнить проверку путем составления и решения системы уравнений для новой системы координат.
Методические указания и пример расчета
Дано:Плита,
закрепленная на шести стержнях, находится
в равновесии под действием двух активных
сил: составляющей угол
составляющей угол с
осьюxв плоскости
(z,x)
и силы тяжести
с
осьюxв плоскости
(z,x)
и силы тяжести Известны размеры
Известны размеры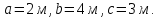
Определить:усилия в стержнях
 Выполнить
проверку.
Выполнить
проверку.

Рис. 6.7 Схема заданных сил и закрепления плиты
Решение:
Полагая
стержни растянутыми, приложим к плите
усилия со стороны отброшенной части
стержней с нижними опорами (Рис. 6.8).
Обозначим два острых угла
 ,
которые наклонные стержни составляют
с вертикалью. Определим их значения в
градусах:
,
которые наклонные стержни составляют
с вертикалью. Определим их значения в
градусах:

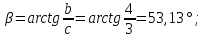
 Рис. 6.8 Схема заданных сил и реакций
связей
Рис. 6.8 Схема заданных сил и реакций
связей
Составим систему уравнения равновесия в осях (x,y,z):

Перенесем активные силы в правую часть уравнений, меняя при этом знак.

Представим систему уравнений равновесия в матричной форме

Обозначим матрицу в левой части системы

 ;
;
вектор-столбец в правой части системы
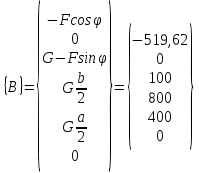 ;
;
и вектор-столбец неизвестных

Тогда система уравнений запишется в компактной форме

Решение
системы сводится к отысканию вектор-столбца
неизвестных реакций стержней Для
определения реакций стержней воспользуемся
методом Гаусса решения систем линейных
уравнений методом исключения. Существуют
стандартные программы решения системы
линейных алгебраических уравнений
методом Гаусса без нахождения обратной
матрицы к матрице жесткости (SIMQ“Fortrun”). Используем
аналогичную подпрограмму на языкеC#
(ПРИЛОЖЕНИЕ 5).
Для
определения реакций стержней воспользуемся
методом Гаусса решения систем линейных
уравнений методом исключения. Существуют
стандартные программы решения системы
линейных алгебраических уравнений
методом Гаусса без нахождения обратной
матрицы к матрице жесткости (SIMQ“Fortrun”). Используем
аналогичную подпрограмму на языкеC#
(ПРИЛОЖЕНИЕ 5).
Единственная форма проекта в конструкторе имеет вид:

Рис. 6.9 Форма проекта в конструкторе
При запуске проекта на выполнение и подстановке исходных данных результат расчетов появляется в нижней таблице:

Рис. 6.10 Форма проекта при запуске программы
Для
проверки правильности решения задачи
перенесем систему координат в нижний
ярус конструкции и составим новую
систему уравнений в осях
 :
:

Возможно
использовать эти уравнения для подстановки
в них найденных сил, при правильном
решении, уравнения должны обращаться
в тождества. Другой способ проверки
заключается в повторном нахождении
неизвестных из новых уравнений равновесия
в системе координат
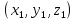 и сравнении их с ранее найденными в
системе координат
и сравнении их с ранее найденными в
системе координат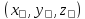 .
Используем второй способ.
.
Используем второй способ.
Перенесем активные силы в правую часть уравнений, меняя при этом знак.

Представим систему уравнений равновесия в матричной форме


Обозначим матрицу в левой части системы

 ;
;
вектор-столбец в правой части системы
 ;
;
Результат вычислений представлен на форме:
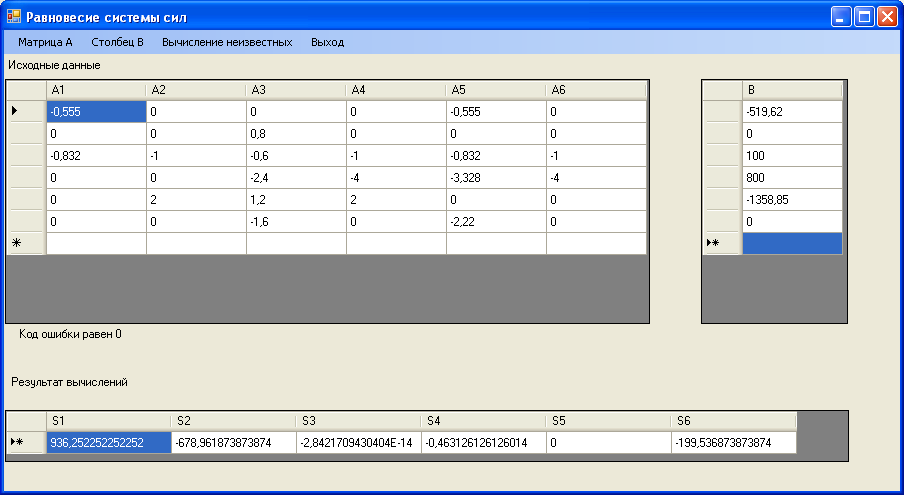
Рис. 6.11 Форма проекта с проверкой.
Есть
отклонения в результатах расчетных
усилий
 ,
, , которые менее 0,2 % от усредненных
значений искомых сил.
, которые менее 0,2 % от усредненных
значений искомых сил.
Варианты заданий
Варианты: 1, 2, 3, 4 (Рис. 6.12)
Дано:Плита,
закрепленная на шести стержнях, находится
в равновесии под действием двух активных
сил: составляющей угол
составляющей угол с
осьюx и лежащей
в плоскости параллельной плоскости
(z,x)и силы тяжести
с
осьюx и лежащей
в плоскости параллельной плоскости
(z,x)и силы тяжести Известны размеры
Известны размеры
Вариант 1: Сила Fприложена в точкеA;
Вариант 2: Сила Fприложена в точкеB;
Вариант 3: Сила Fприложена в точкеC;
Вариант 4: Сила Fприложена в точкеD
Определить:усилия в стержнях
Выполнить проверку.

Рис. 6.12 Схема к вариантам заданий 1,2,3,4.
Варианты: 5,6,7,8 (Рис. 6.13)
Дано:Плита,
закрепленная на шести стержнях, находится
в равновесии под действием двух активных
сил: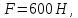 составляющей угол
составляющей угол с
осьюy и лежащей
в плоскости параллельной плоскости
(y,z)и силы тяжести
с
осьюy и лежащей
в плоскости параллельной плоскости
(y,z)и силы тяжести Известны размеры
Известны размеры
Вариант 5: Сила Fприложена в точкеA;
Вариант 6: Сила Fприложена в точкеB;
Вариант 7: Сила Fприложена в точкеC;
Вариант 8: Сила Fприложена в точкеD
Определить:усилия в стержнях
Выполнить проверку.

Рис.6.13. Схема к вариантам заданий 5,6,7,8.
Варианты: 9,10,11,12. (Рис. 6.14)
Дано:Плита,
закрепленная на шести стержнях, находится
в равновесии под действием двух активных
сил: составляющей угол
составляющей угол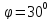 с
осьюx и лежащей в
плоскости (x,y)и силы тяжести
с
осьюx и лежащей в
плоскости (x,y)и силы тяжести Известны размеры
Известны размеры
Вариант 9: Сила Fприложена в точкеA;
Вариант 10: Сила Fприложена в точкеB;
Вариант 11: Сила Fприложена в точкеC;
Вариант 12: Сила Fприложена в точкеD
Определить:усилия в стержнях
Выполнить проверку.

Рис. 6.14. Схема к вариантам заданий 9,10,11,12.
Содержание отчета
Постановка задачи для конкретного варианта.
Расчетные уравнения в развернутой и в матричной форме (в символьном виде и с подстановкой численных значений), сопровождая уравнения подробными расчетными схемами.
Текст клиентского кода программы.
Результаты выполнения программы (экранные формы).
