4. Формирование матриц жесткости и масс в глобальной системе координат для рамы

Узловые перемещения рамного конечного элемента в локальной системе координат 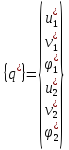выражаются через глобальные узловые обобщенны перемещенияи углы α и β рис.4.1 в виде

Рис. 4.1. Преобразование на плоскости узловых перемещений рамного конечного элемента

В матричной форме это преобразование запишем так

где

(4.2)

Направляющие косинусы локальной оси определяются глобальными координатами узлов

(4.3)

(4.4)

где

(4.5)

длина элемента.

Матрица жесткости конечного элемента в глобальной системе координат преобразуется с учетом выражения (4.1) и зависимости для потенциальной энергии элемента, которая не зависит от выбора системы отсчета:

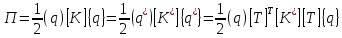
тогда

(4.6)

Аналогично преобразуется и матрица масс конечного элемента , на основании того, что кинетическая энергия элемента не зависит от направления осей координат, по аналогии с потенциальной энергией получим:

(4.7)

Узловые силы и моменты, приложены к узлам рамы, которые задаются в глобальной системе координат, в преобразованиях не нуждаются.

Силы, заданные в локальной системе отсчета для каждого элемента должны быть приведены к глобальной системе отсчета. Распределенные нагрузки приведенные к узловым силам в локальной системе координат совершают возможную работу на глобальных возможных перемещениях

,

где узловые силы в локальной системе отсчета равны

Выразим глобальные перемещения через локальные по уравнениям (4.1):

,

учитывая

,

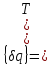или

,

тогда

,

Коэффициенты в выражении возможной работы при вариациях обобщенных координат есть вклад в обобщенные силы от распределенных внешних нагрузок

(4.8)

Добавляя в выражение (4.8) вклад сил заданных в глобальной системе отсчета и объединяя уравнения равновесия для всей совокупности конечных элементов, получим уравнения равновесия системы при статической задаче:

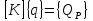(4.9)

И уравнения динамического равновесия для движения всей конструкции:

(4.10)

Рассмотрим, как формируется матрица жесткости и уравнения равновесия для механической системы, содержащей рамные конечные элементы (рис. 4.2), к которой приложены распределенные силы интенсивности p=400 Н/м и сосредоточенные силаF=700 Н и моментM=200 Нм. Известны размерыБез учета закрепления узлов необходимо ввести 24 обобщенных перемещений (по три на каждый из 8 узлов). Матрица жесткости для такой системы будет иметь размер 2424, а матрица каждого элемента, приведенная к глобальной системе координат, имеет размер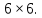Таким образом, конечные элементы, узлы которых совпадают должны вносить общий суммарный вклад в соответствующие элементы матрицы жесткости, причем шарнирно-соединенные элементы получают в точке соединения разные глобальные номера узлов. Это обусловлено тем, что углы поворота таких узлов разные.

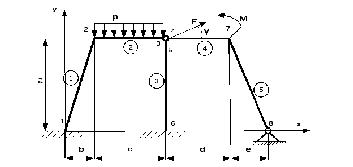
Рис. 4.2 Рама с номерами узлов: 1...8 и номерами стержней 1...5 (в окружностях)

Рис. 4.3 Нумерация глобальных обобщенных координат для трех первых элементов с указанием в скобках номеров внутренней нумерации

В качестве исходных данных для формирования матрицы жесткости потребуется координатная матрица для узлов и топологическая матрица для конечных элементов. Координатная матрица – это таблица, которая содержит информацию о номере узла и его координатах, а также о способе его закрепления и приложенных сосредоточенных силовых воздействиях. В соответствии с количеством узлов выбирается число обобщенных перемещений.

Для конструкции рисунка 4.2 с учетом размеровкоординатная матрица имеет вид таблицы 4.1.

Таблица 4.1