
- •Интегральное исчисление
- •Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Определенный интеграл
- •Свойства определенного интеграла
- •2.2 Интегрирование методом замены переменной и по частям в определенном интеграле
- •Несобственные интегралы с бесконечными пределами
- •Геометрические и физические приложения определенного интеграла
- •Контрольные вопросы и задания
Свойства определенного интеграла
По определению,
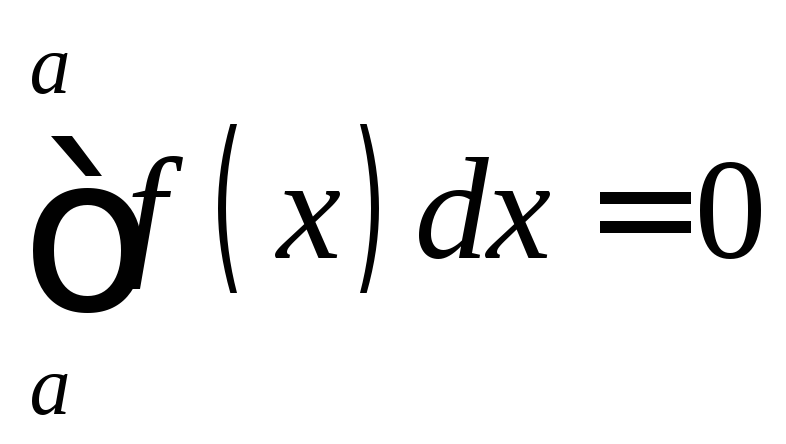 .
. .
. .
. .
. (свойство
аддитивности).
(свойство
аддитивности).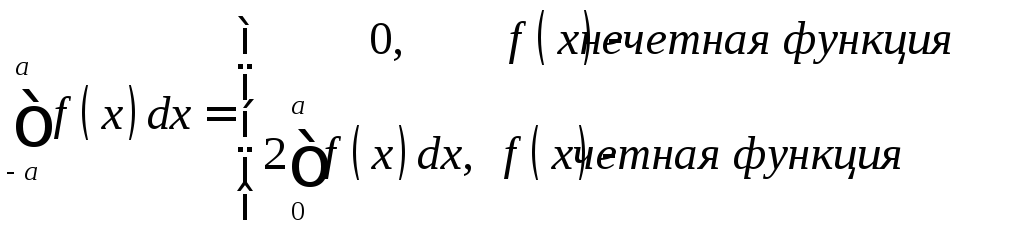 .
.Теорема о среднем. Если функция
 непрерывна на
непрерывна на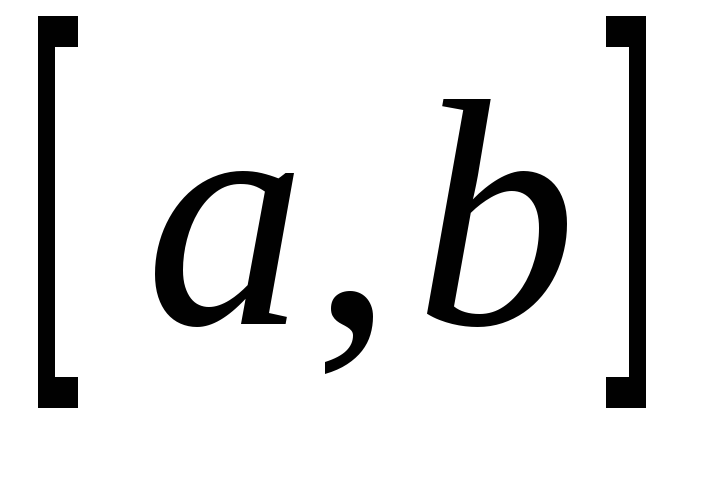 ,
то существует точка
,
то существует точка такая, что
такая, что .
Число
.
Число называетсясредним
значением
функции
называетсясредним
значением
функции
 на отрезке
на отрезке .
.
Пример 1. Вычислить
интеграл
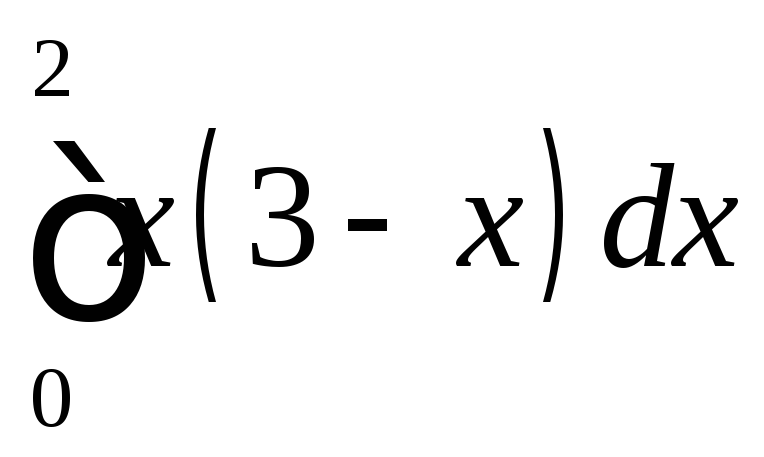 .
.
Раскроем скобки и по свойствам 1 и 2 определенного интеграла получим:
 .
.
Пример 2.
Вычислить интеграл
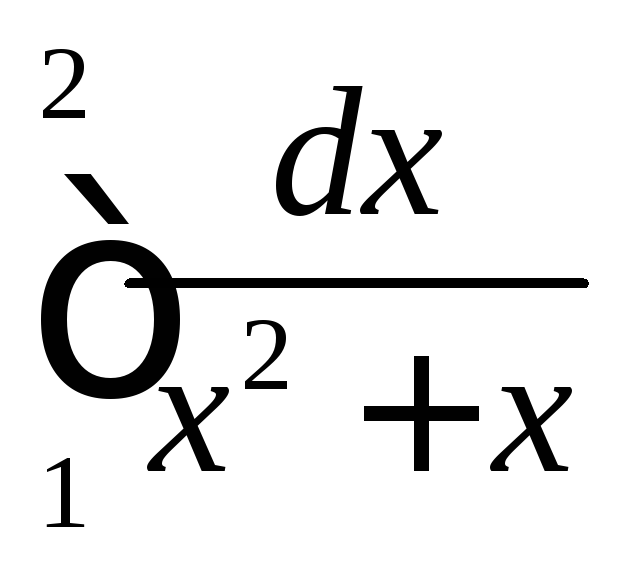 .
.
Разложим знаменатель
на множители, к 1 в числителе прибавим
и вычтем
![]() и разделим почленно числитель на
знаменатель:
и разделим почленно числитель на
знаменатель:

![]() .
.
Заметим, что данный интеграл можно найти методом неопределенных коэффициентов, разложив подынтегральную функцию на простейшие дроби.
2.2 Интегрирование методом замены переменной и по частям в определенном интеграле
Формулы замены переменной и интегрирования по частям в определенном интеграле аналогичны соответствующим формулам (1) и (2) в неопределенном интеграле:
 –(4)
–(4)
формула замены
переменной в определенном интеграле,
где
![]() и
и![]() – непрерывно дифференцируемая функция
на отрезке
– непрерывно дифференцируемая функция
на отрезке![]() .
.
Напомним, что формула часто применяется в обратном порядке:
 ,
где
,
где
![]() .
.
Замена пределов
интегрирования позволяет после нахождения
первообразной подынтегральной функции
не делать обратную подстановку, а
подставить новые пределы интегрирования
вместо переменной
![]() ,
которые определяются из соответствующих
равенств.
,
которые определяются из соответствующих
равенств.
Пример 1. Вычислить
интеграл
 .
.
Пусть
![]() ,
тогда
,
тогда![]() ;
;![]() ,
тогда
,
тогда![]() .
.
 .
.
 –(5)
–(5)
формула интегрирования
по частям в определенном интеграле, где
![]() – непрерывно дифференцируемые функции
на отрезке
– непрерывно дифференцируемые функции
на отрезке![]() .
.
Пример 2. Вычислить
интеграл
 .
.

![]() .
.
Несобственные интегралы с бесконечными пределами
Обобщим понятие определенного интеграла на случай, когда промежуток интегрирования является бесконечным.
Пусть функция
![]() определена на промежутке
определена на промежутке![]() и интегрируема на любом отрезке
и интегрируема на любом отрезке![]() .
.
Если существует
конечный предел
 ,
то он называетсянесобственным
интегралом с бесконечным верхним
пределом
(1-го рода) и обозначается
,
то он называетсянесобственным
интегралом с бесконечным верхним
пределом
(1-го рода) и обозначается
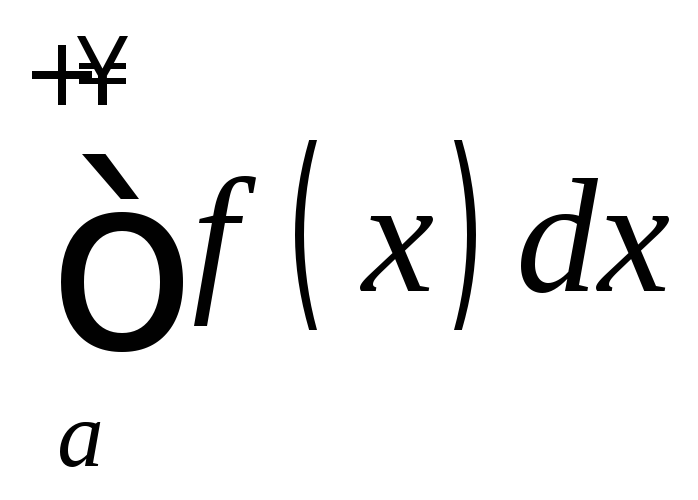 .
.
Таким образом, по определению
 .
(6)
.
(6)
В этом случае
говорят, что несобственный интеграл
 сходится.
сходится.
Если предел
 не существует или равен бесконечности,
то говорят, что интеграл
не существует или равен бесконечности,
то говорят, что интеграл расходится.
расходится.
Аналогично
определяется несобственный интеграл
на промежутке
![]() :
:
 –несобственный
интеграл с бесконечным нижним пределом.
–несобственный
интеграл с бесконечным нижним пределом.
По определению, несобственный интеграл с бесконечными пределами
 ,
,
где
![]() – произвольное действительное число.
– произвольное действительное число.
В этом случае
интеграл
 сходится, если сходятся оба интеграла
правой части.
сходится, если сходятся оба интеграла
правой части.
Примеры.
Вычислить несобственные интегралы или установить их расходимость:
![]() ,
т.к.
,
т.к.
![]() .
Интеграл
расходится.
.
Интеграл
расходится.
 .
.
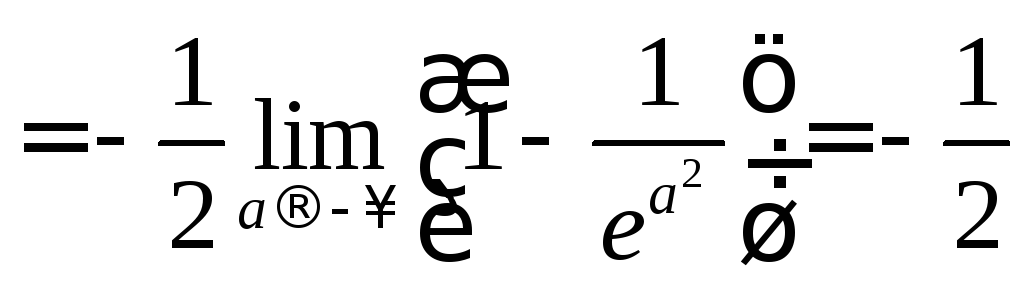 ,
т.к.
,
т.к.
 .
.
Геометрические и физические приложения определенного интеграла
Площадь плоской фигуры.
Вычисление площадей плоских фигур основано на геометрическом смысле определенного интеграла.
Площадь плоской фигуры, ограниченной кривой
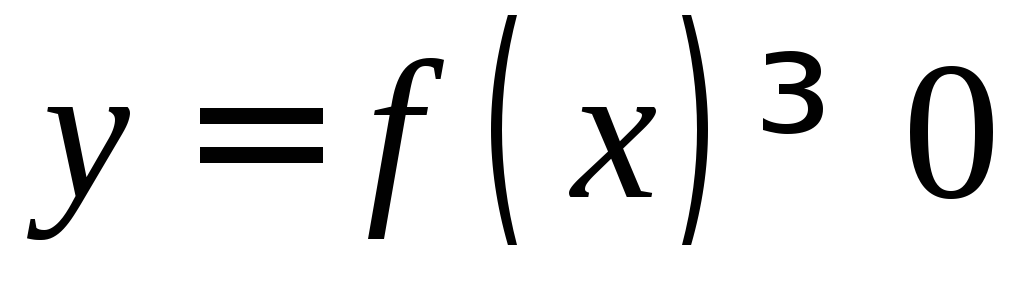 ,
осью
,
осью и прямыми
и прямыми (рис. 1), находится по формуле
(рис. 1), находится по формуле
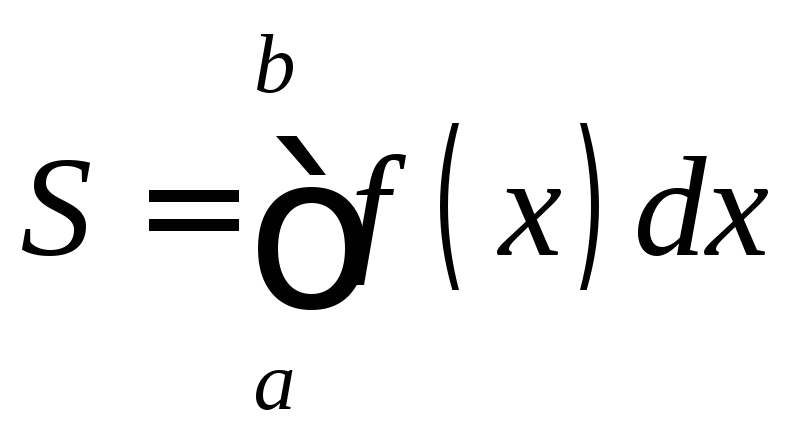 .
(7)
.
(7)
Такую фигуру называют криволинейной трапецией.

Замечание. Если
![]() ,
то
,
то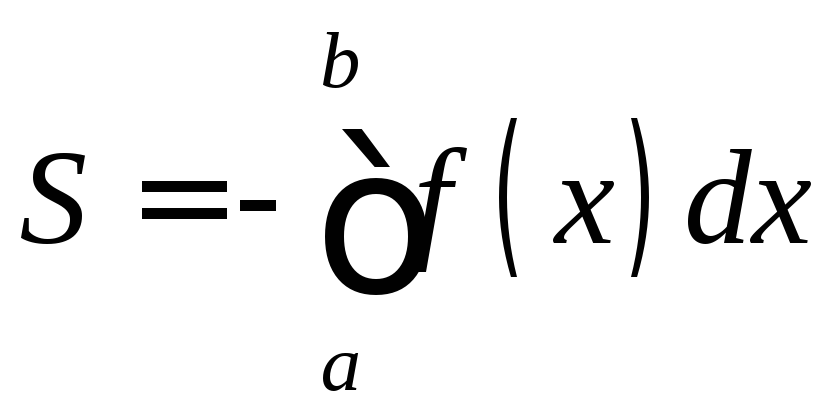 .
.
Площадь плоской фигуры, ограниченной кривыми
 и прямыми
и прямыми (рис. 2), находится по формуле
(рис. 2), находится по формуле
 .
(8)
.
(8)

В некоторых случаях
удобно использовать формулы, аналогичные
формулам (7) и (8), считая
![]() функцией от
функцией от![]() .
.
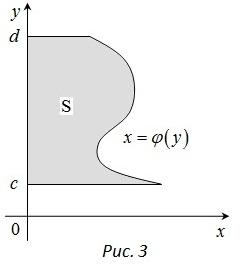
Площадь плоской фигуры, ограниченной кривой
 ,
осью
,
осью и прямыми
и прямыми (рис. 3), находится по формуле
(рис. 3), находится по формуле
 .
(9)
.
(9)
Площадь плоской фигуры, ограниченной кривыми
 и прямыми
и прямыми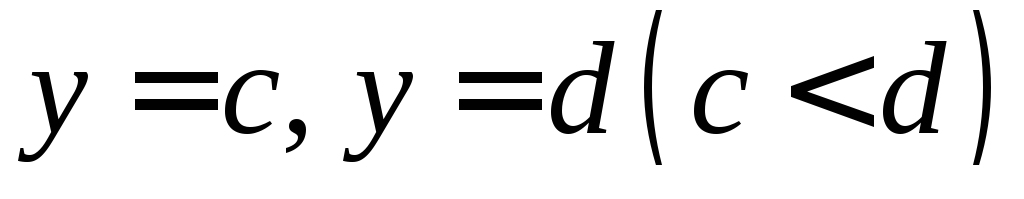 ,
находится по формуле
,
находится по формуле
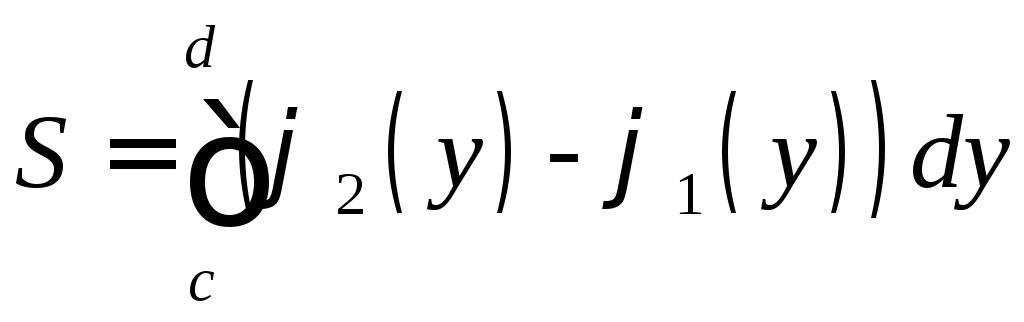 .
(10)
.
(10)
Пример 1. Вычислить
площадь фигуры, ограниченной линиями
![]() .
.
Абсцисса точки
пересечения линий
![]() (парабола
(парабола![]() ,
смещенная вправо на 2 единицы) и
,
смещенная вправо на 2 единицы) и![]() (прямая, проходящая через начало координат
под углом
(прямая, проходящая через начало координат
под углом![]() к оси
к оси![]() )
находится подбором:
)
находится подбором:![]() .
Фигура, ограниченная данными кривыми
состоит из двух частей, заданных на
отрезках
.
Фигура, ограниченная данными кривыми
состоит из двух частей, заданных на
отрезках![]() и
и![]() ,
поэтому ее следует разбить на части,
найти площадь каждой области и полученные
результаты сложить (свойство 5 определенного
интеграла). Каждая из площадей находится
по формуле (7).
,
поэтому ее следует разбить на части,
найти площадь каждой области и полученные
результаты сложить (свойство 5 определенного
интеграла). Каждая из площадей находится
по формуле (7).
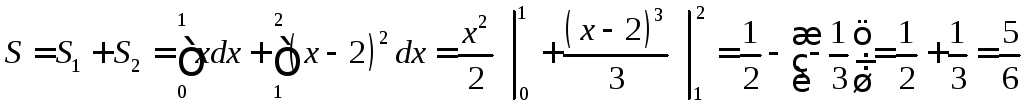 .
.
Пример 2. Вычислить
площадь фигуры, ограниченной линиями
![]() .
Сделать чертеж.
.
Сделать чертеж.
Для данных кривых
(парабола, ветви которой направлены
вправо, и прямая, рис. 4) наиболее
рационально найти ординаты
точек пересечения, решив систему
уравнений:
 .
.

На отрезке
 выполняется
выполняется![]() ,
тогда площадь фигуры находим по формуле
(10):
,
тогда площадь фигуры находим по формуле
(10):

Объем тела вращения.
Рассмотрим вращение плоских фигур вокруг координатных осей прямоугольной декартовой системы координат.
Объем тела, образованного вращением вокруг оси
 фигуры, ограниченной кривой
фигуры, ограниченной кривой ,
осью
,
осью и прямыми
и прямыми ,
находится по формуле
,
находится по формуле
 .
(11)
.
(11)
Объем тела, образованного вращением вокруг оси
 фигуры, ограниченной кривыми
фигуры, ограниченной кривыми и прямыми
и прямыми ,
находится по формуле
,
находится по формуле
 .
(12)
.
(12)
Объем тела, образованного вращением вокруг оси
 фигуры, ограниченной кривой
фигуры, ограниченной кривой ,
осью
,
осью и прямыми
и прямыми ,
находится по формуле
,
находится по формуле
 .
(13)
.
(13)
Объем тела, образованного вращением вокруг оси
 фигуры, ограниченной кривыми
фигуры, ограниченной кривыми и прямыми
и прямыми ,
находится по формуле
,
находится по формуле
 .
(14)
.
(14)
Пример 1. Найти
объем тела, образованного вращением
фигуры, ограниченной линиями
![]() ,
вокруг: а) оси
,
вокруг: а) оси![]() ;
б) оси
;
б) оси![]() .
Сделать чертеж.
.
Сделать чертеж.
Фигура (криволинейная
трапеция) ограничена ветвью параболы
![]() и прямыми
и прямыми![]() .
.
а) Построим тело (рис. 5).

Тогда по формуле (11):
 .
.
б) Построим тело (рис. 6).

Тогда по формуле (14):
 .
.
Пример 2. Найти
объем тела, образованного вращением
фигуры, ограниченной линиями
![]() ,
вокруг оси
,
вокруг оси![]() .
.
Найдем абсциссы
точек пересечения кривых. Для этого
решим систему уравнений:
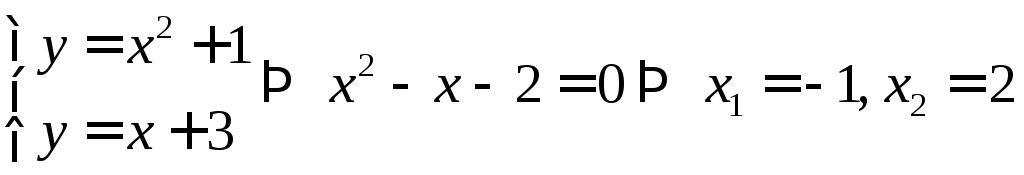 .
.
На отрезке
![]() выполняется
выполняется![]() ,
тогда объем тела находим по формуле
(12):
,
тогда объем тела находим по формуле
(12):


 .
.
Длина дуги плоской кривой.
Рассмотрим случаи, когда кривая задана явно и параметрически.
Длина дуги плоской кривой, заданной уравнением
 на отрезке
на отрезке ,
находится по формуле
,
находится по формуле
 ,
(15)
,
(15)
где
![]() – непрерывно дифференцируемая функция
на
– непрерывно дифференцируемая функция
на![]() .
.
Длина дуги плоской кривой, заданной уравнениями
 на отрезке
на отрезке ,
находится по формуле
,
находится по формуле
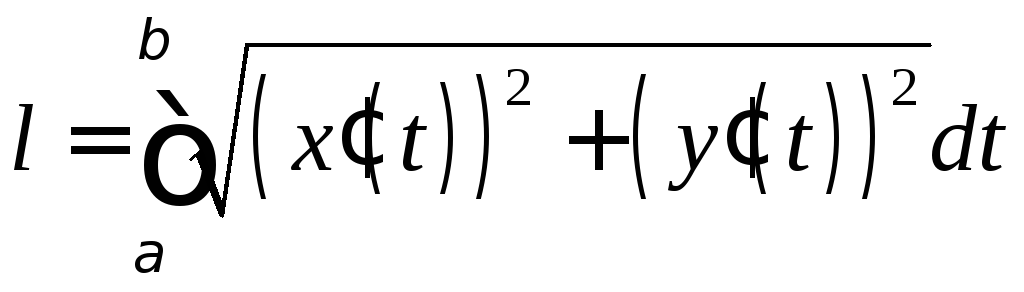 ,
(16)
,
(16)
где
![]() – непрерывно дифференцируемые функции
на
– непрерывно дифференцируемые функции
на![]() .
.
Пример. Найти
длину дуги кривой
![]() .
.
Данное уравнение
задает окружность, где
![]() .
Найдем четвертую часть длины дуги. Тогда
по формуле (15):
.
Найдем четвертую часть длины дуги. Тогда
по формуле (15):


![]() .
.
Рассмотрим другой
способ решения.
Параметризуем уравнение окружности:
![]() ,
где
,
где![]() .
Тогда длина дуги по формуле (16) равна:
.
Тогда длина дуги по формуле (16) равна:
 .
.
Путь, пройденный телом.
Путь, пройденный
телом за отрезок времени
![]() со скоростью
со скоростью![]() ,
находится по формуле
,
находится по формуле
 .
(17)
.
(17)
Пример. Скорость
автобуса при торможении меняется по
закону
![]() .
Какой путь пройдет автобус от начала
торможения до остановки?
.
Какой путь пройдет автобус от начала
торможения до остановки?
Тело остановится,
если скорость равна нулю, т.е.
![]() ,
тогда
,
тогда![]() .
По формуле (17) находим путь:
.
По формуле (17) находим путь:
 .
.
Работа переменной силы.
Работа переменной
силы
![]() ,
направленной вдоль оси
,
направленной вдоль оси![]() на отрезке
на отрезке![]() ,
находится по формуле
,
находится по формуле
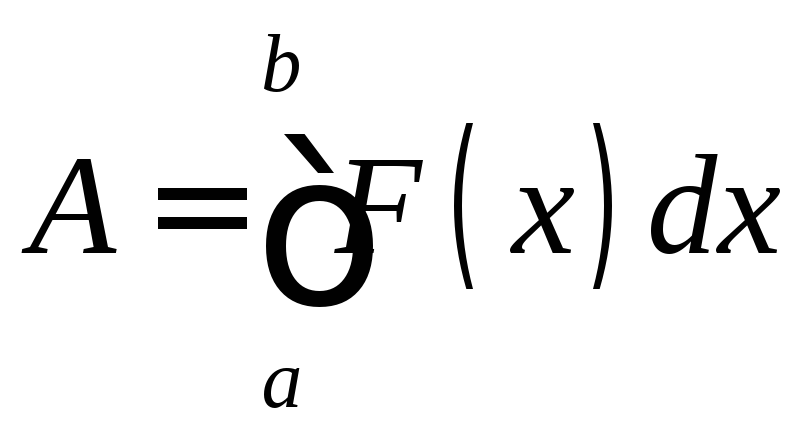 .
(18)
.
(18)
Пример.
Какую
работу надо затратить, чтобы растянуть
пружину на
![]() ,
если сила в
,
если сила в![]() растягивает ее на
растягивает ее на![]() ?
?
По закону Гука
упругая сила, растягивающая пружину,
пропорциональна растяжению, т.е.
![]() ,
где
,
где![]() – коэффициент пропорциональности,
– коэффициент пропорциональности,![]() – растяжение пружины. По условию
– растяжение пружины. По условию![]() .
Тогда по формуле (18) находим работу:
.
Тогда по формуле (18) находим работу:
 .
.
Масса неоднородного стержня.
Масса неоднородного
стержня линейной плотности
![]() на отрезке
на отрезке![]() ,
находится по формуле
,
находится по формуле
 .
(19)
.
(19)
Пример.
Найти
массу стержня длины
![]() ,
если линейная плотность стержня меняется
по закону
,
если линейная плотность стержня меняется
по закону![]() ,
где
,
где![]() – расстояние от одного из концов стержня.
– расстояние от одного из концов стержня.
Массу стержня находим по формуле (19):
 .
.



