2. Интегрирование рациональных дробей

Рациональной дробью (дробно-рациональной функцией) называется отношение многочленов , гдеи– степени многочленов.

Например, – многочлен степени.

Степень одночлена, представляющего собой действительное число, равна нулю.

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя , иначе –неправильной.

Например,

1. –неправильные дроби;

2. –правильные дроби.

Всякая неправильная рациональная дробь может быть представлена в виде суммы многочлена и правильной рациональной дроби. Такое преобразование называется выделением целой части неправильной дроби и может быть выполнено делением числителя на знаменатель по правилу деления многочлена на многочлен.

Например, , т.к.

В некоторых случаях целую часть неправильной дроби можно выделить с помощью элементарных преобразований.

Например, .

Всякая правильная рациональная дробь может быть представлена в виде суммы простейших дробей следующих четырех типов:

,

где и,, многочленне имеет действительных корней.

Для того чтобы правильную рациональную дробь представить в виде суммы простейших дробей, надо найти корни многочлена, т.е. решить уравнение, и разложить знаменатель на множители (многочлены первой степени и многочлены второй степени, не имеющие действительных корней, с действительными коэффициентами):

,

где – коэффициент многочленапри,,.

Степени показывают, сколько раз линейные и квадратичные множители входят в разложение. Линейному множителю видасоответствует действительный коренькратности; если, то – простой корень. Квадратичному множителю видасоответствует пара комплексно-сопряженных корней кратности.

Например,

1. .

Напомним, если – действительные корни квадратного трехчлена, то.

2. .

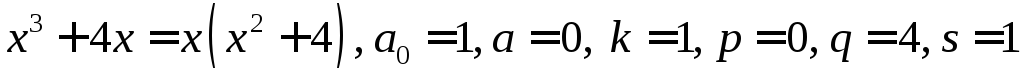Тогда в разложении правильной дроби:

1. каждому множителю вида будет соответствовать сумма простейших дробейитипа:,

2. каждому множителю вида – сумма простейших дробейитипа:.

Например, разложение правильной дроби на простейшие дроби:

1. ;

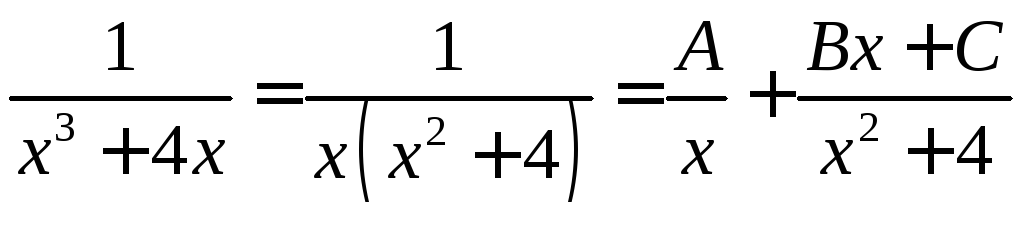2. , где – неопределенные коэффициенты.

Неизвестные коэффициенты в разложении правильной рациональной дроби можно найти методом неопределенных коэффициентов. Для этого надо правую часть привести к общему знаменателю, приравнять коэффициенты при одинаковых степеняхмногочлена числителя левой части и получившегося многочлена числителя правой части и решить линейную систему. Заметим, что неизвестные коэффициенты можно также определить, придаваяконкретные значения (обычно значения действительных корней многочлена). В этом случае для нахождения неизвестных коэффициентов, надо приравнять значения соответствующих многочленов.

Правило интегрирования рациональных дробей

1. Определить вид рациональной дроби. Если дробь неправильная, выделить целую часть.

2. Разложить знаменатель правильной рациональной дроби на линейные и квадратичные множители и представить ее в виде суммы простейших дробей с неопределенными коэффициентами.

3. Найти неизвестные коэффициенты.

4. Проинтегрировать целую часть (многочлен) и сумму простейших дробей с найденными коэффициентами.

Пример 1. Найти интеграл .

Разложим правильную дробь на простейшие дроби (см. выше):

.

Запишем правую часть по степеням :и составим систему:. Тогда

.

Покажем, как можно найти неизвестные коэффициенты идругим способом. Рассмотрим тождество .

Пусть , тогда.

Пусть , тогда.

Пример 2. Найти интеграл .

Разложим правильную дробь на простейшие дроби (см. выше):

.

Запишем правую часть по степеням :и составим систему:. Тогда

.

Пример 3. Найти интеграл .

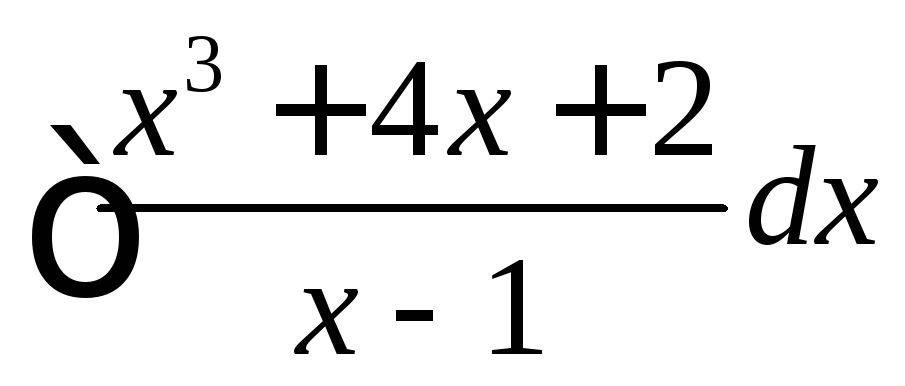Выделим целую часть неправильной дроби (см. выше):

.

Пример 4. Найти интеграл .

Выделим в знаменателе полный квадрат, получим простейшую дробь II типа:

.

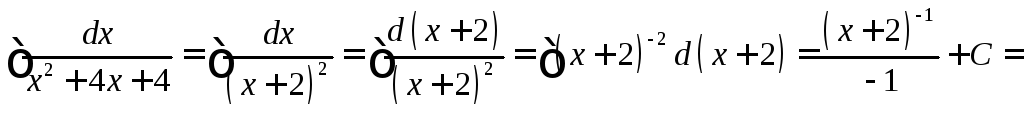
Пример 5. Найти интеграл (простейшая дробьтипа, т.к.).

Выделим в числителе производную знаменателя :

.

Заметим, что многочлен не имеет действительных корней, поэтому для всехпринимает положительные значения и.

Пример 6. Найти интеграл .

Разложим знаменатель правильной дроби на множители: . Здесь– простой корень,– корень кратности, тогда

.

Пусть , тогда.

Пусть , тогда.

Найдем коэффициент . Придадимкакое-нибудь значение, например,, тогда. С учетом найденных значенийиполучим, т.е..

.