Рыночная стоимость облигации через 3,5 года после ее покупки будет

P_t = = 119,2231(д.е.)

Таким образом, стоимость инвестиции в облигацию через 3,5 года после ее покупки составит 76,0486 + 119,2231 = 195,2717 (д.е.).

Теперь предположим, что в момент покупки облигации t = 0 временная структура процентных ставок такова, что безрисковые процентные ставки для всех сроков одинаковы и равны r. Рассмотрим стоимость инвестиции в облигацию через t лет после покупки для двух случаев:

1) временная структура процентных ставок остается неизменной до погашения облигации;

2) сразу после покупки облигации безрисковые процентные ставки для всех сроков мгновенно изменились на одну и ту же величину и стали равными , а затем уже не менялись.

Стоимость инвестиции в облигацию в момент t в первом случае называют планируемой и обозначают через P(r,t), во втором случае – фактической и обозначают через P(, t).

Свойства планируемой и фактической стоимостей инвестиции.

1. P(r, t) и P(, t) – непрерывные возрастающие функции времени:

P(r, t) = , (12.5)

P(, t) =. (12.6)

Действительно, согласно (12.2),

P(r, t) = R_t(r) + P_t(r).

Здесь R_t(r) – результат реинвестирования на момент t поступивших до этого момента платежей от облигации по ставке r, P_t(r) – планируемая рыночная цена облигации через t лет после покупки. Пусть t₁, t₂,…, t_m, t_{m + 1},…, t_n – моменты поступления платежей С₁, С₂,…, С_m , С_m+1,…, С_n соответственно и t [t_m, t_m+1]. Тогда планируемая стоимость инвестиции

P(r, t) = + =

= = .

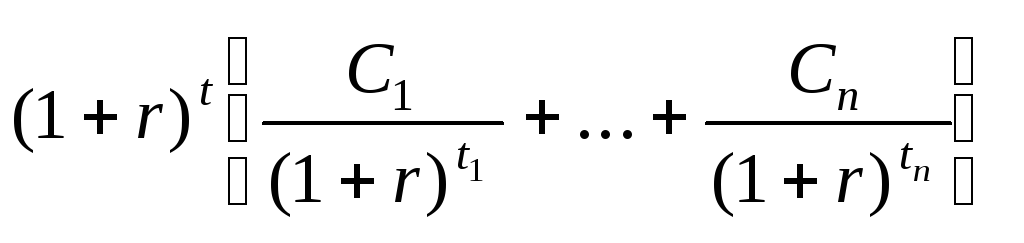Здесь

P(r) =

– рыночная цена покупки облигации в момент t = 0, соответствующая существующей на этот момент времени временной структуре процентных ставок.

Фактическая стоимость инвестиции в момент t согласно (12.2), равна

P(, t) = R_t() + P_t().

Здесь R_t() – результат реинвестирования на момент t поступивших до этого момента платежей от облигации по ставке , P_t() – фактическая рыночная цена облигации через t лет после покупки. Выражение (12.6) для фактической стоимости инвестиции получаем аналогично:

P(, t) = + =

= = .

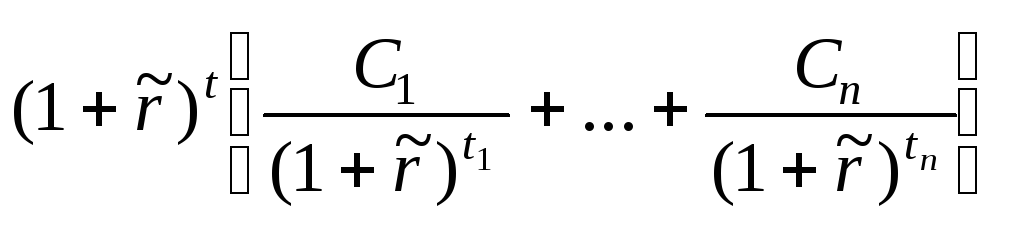Здесь

P() =

– оценка облигации на момент t = 0, соответствующая новой временной структуре процентных ставок сразу после покупки облигации.

(12.5) и (12.6) – это показательные функции времени, основания которых больше единицы. Из элементарной математики известно, что такая функция является непрерывной и возрастающей.

2. Существует и притом единственный момент времени t*, когда фактическая стоимость инвестиции равна планируемой.

Доказательство. Пусть > r. Рассмотрим момент t = 0. Тогда P() < P(r) (см. зависимость цена – доходность, теорема 9.1), или

P(, 0) < P(r, 0). (12.7)

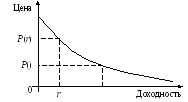
Рис. 1.12.1

Рассмотрим теперь момент погашения облигации t = t_n. Тогда

P(r, t_n) = ,

P(, t_n) = .

Так как > r, то

P(, t_n) > P(r, t_n). (12.8)

Из неравенств (12.7) и (12.8) следует, что существует такой момент времени t*, когда P(, t*) = P(r, t*). Покажем, что момент t* является единственным. Предположим, что равенство стоимостей достигается в точках τ₁ и τ₂. Следовательно

P(,τ₁) = P(r, τ₁) и P(,τ₂) = P(r, τ₂).

= и = .

Тогда

.

Отсюда τ₁ = τ₂ = t*.

Рис. 1.12.2

Случай, когда < r, доказывается аналогично. Найдем t*.

P(, t*) = P(r, t*),

= ,

.

Отсюда

t* = 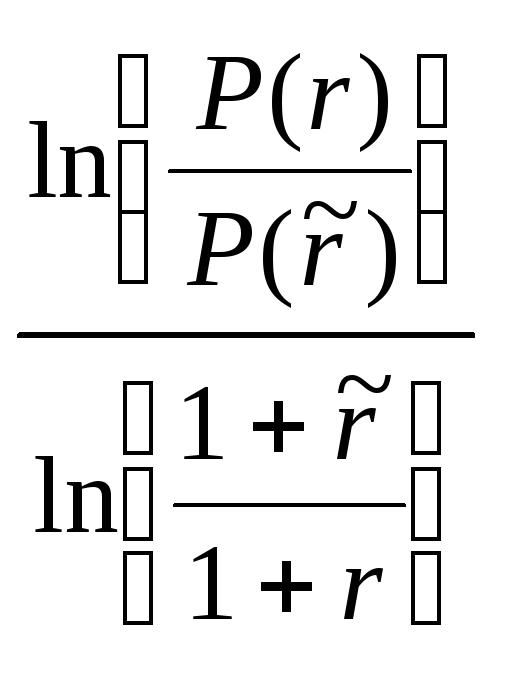. (12.9)