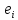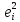ГОУ ВПО
"Российский Экономический университет имени Г.В.Плеханова"
Кафедра
"Математические методы в экономике"
Контрольная работа
по дисциплине
"Эконометрика"
Выполнил:
студент финансового факультета
гр. 2312
Чупрак Д. А.
Проверил:
Колпаков В. Ф.
Москва – 2010
Задача 5. По территориям региона известны данные за 2006 год.
Задание.
-
Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.
-
Оцените по МНК параметры уравнения линейной регрессии.
-
Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.
-
Проверьте качество уравнения регрессии:
-
значимость коэффициентов регрессии;
-
интервальные оценки коэффициентов регрессии;
-
значимость уравнения регрессии в целом.
-
-
Проинтерпретируйте результаты.
-
Сделайте прогноз размера пенсий при значении прожиточного минимума Х = Хпрогн..
Вариант 5.4 (Северный и Северозападный регионы)
|
Номер района |
Средний размер назначенных ежемесячных пенсий, тыс. руб., Y |
Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., Х |
|
1 |
3,8 |
1,8 |
|
2 |
3,8 |
1,9 |
|
3 |
4,1 |
2,4 |
|
4 |
4,0 |
2,1 |
|
5 |
4,5 |
2,7 |
|
6 |
4,3 |
2,0 |
|
7 |
4,6 |
2,6 |
|
8 |
4,2 |
2,5 |
Хпрогн=
3; Уровень значимости
=
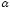0,07.
-
Построим корреляционное поле с помощью Мастера диаграмм, используя данные по средней заработной плате и доле денежных доходов в Дальневосточном регионе.
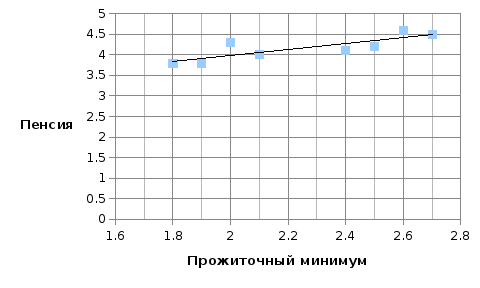
По данному расположению точек можно сделать предположение о наличии линейной зависимости между среднемесячной заработной платой и долей денежных доходов.
-
МНК. Оценка параметров уравнения линейной регрессии.
|
i |
|
|
|
x*y |
|
|
|
|
|
1 |
1,8 |
3,8 |
3,24 |
6,84 |
14,44 |
3,841 |
-0,041 |
0,002 |
|
2 |
1,9 |
3,8 |
3,61 |
7,22 |
14,44 |
3,913 |
-0,113 |
0,013 |
|
3 |
2,4 |
4,1 |
5,76 |
9,84 |
16,81 |
4,270 |
-0,170 |
0,029 |
|
4 |
2,1 |
4 |
4,41 |
8,4 |
16 |
4,055 |
-0,055 |
0,003 |
|
5 |
2,7 |
4,5 |
7,29 |
12,15 |
20,25 |
4,484 |
0,016 |
0,000 |
|
6 |
2 |
4,3 |
4 |
8,6 |
18,49 |
3,984 |
0,316 |
0,100 |
|
7 |
2,6 |
4,6 |
6,76 |
11,96 |
21,16 |
4,412 |
0,188 |
0,035 |
|
8 |
2,5 |
4,2 |
6,25 |
10,5 |
17,64 |
4,341 |
-0,141 |
0,020 |
|
Сумма |
18 |
33,3 |
41,32 |
75,51 |
139,23 |
|
0,000 |
0,201 |
|
Среднее |
2,25 |
4,1625 |
5,165 |
9,43875 |
17,40375 |
|
|
|
;
.
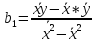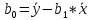Рассчитаем коэффициенты уравнения линейной регрессии двумя способами.
=
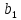0,713415
=
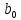2,557317
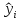= 2,557317 + 0,713415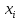
Коэффициент
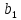показывает тесноту связи между x
и y.
При увеличении зарплаты на единицу,
прирост сбережений будет составлять
0,713415.
-
Выборочный коэффициент корреляции
;
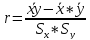
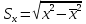0,32016
;
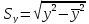0,27811
r = 0,82128
Полученное значение говорит о довольно сильной связи между пенсией и минимальным прожиточным минимумом. Число положительное, а значит связь тоже положительная (заработная плата и доля денежных доходов увеличиваются прямопропорционально).
-
Проверка качества уравнения регрессии.
-
Интерпретация результатов.
По таблице критических
точек Стьюдента, находим
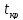= 2,7123 (уровень значимости α = 0,07, в таблицу
входим со значениями: α/2 = 0,035, и ν = n
– 2 = 8 – 2 = 6 степенями свободы).