ЛЕКЦИЯ 5

Теория вероятностей и математическая статистика

Случайные величины

Одномерные случайные величины

Пусть есть случайный эксперимент, ─ пространство элементарных событий.

Определение Случайной величиной называется

функция, отображающая в R.

: R

(То есть = (ω)). Смысл: случайная величина – это

числовая функция, принимающая значения случайным образом.

Дискретные распределения

Определение

Случайная величина имеет дискретное

распределение, если она принимает не более чем счетное число значений.

Значения: a1, a2,…,

Вероятности значений: pi = P( = ai) > 0

pi 1.

i 1

Определение

Если случайная величина имеет

дискретное распределение, то рядом распределения называется соответствие

ai pi, которое имеет вид :

a1 a2 a3 … P p1 p2 p3 …

Пример

Подбрасываем 1 раз кубик. Пусть={1,2,3,4,5,6}, и две функции из в R заданы так: (ω) = ω и (ω) = ω2. Построить ряды распределения.

Решение

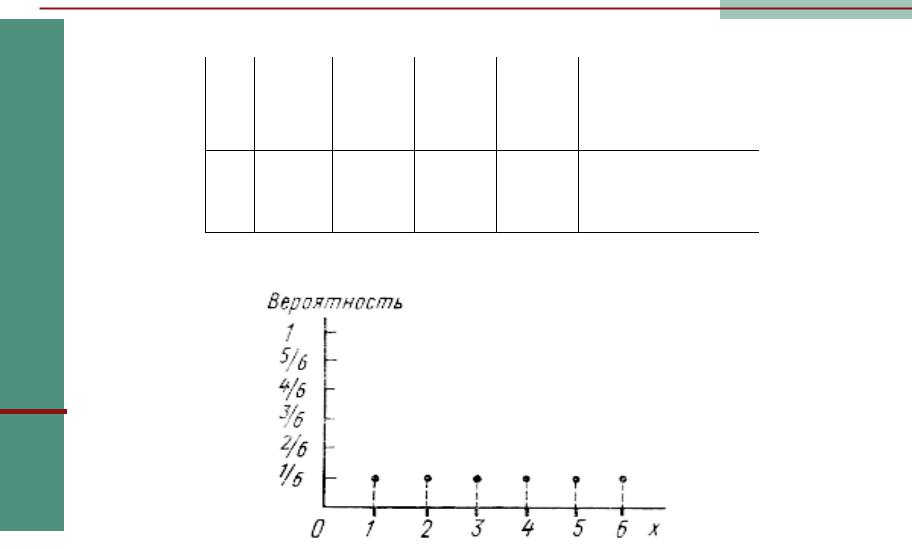
Графическое задание ряда распределения ξ

Примеры дискретных распределений

Вырожденное распределение Ia

Случайная величина имеет вырожденное распределение с параметром a, если принимает единственное значение a с вероятностью 1, т.е. P( = a) = 1. Таблица распределения имеет вид

a P 1

Дискретное равномерное распределение

Случайная величина имеет дискретное равномерное распределение, если принимает n значений х1, х2,..., xn с

вероятностями рi = 1/n.

Распределение Бернулли Bp

Случайная величина имеет распределение Бернулли с параметром p, если принимает значения 1 и 0 с вероятностями p и q = 1 – p, соответственно.

Случайная величина с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха p (0 успехов или 1

успех).

0 1 P q p

Биномиальное распределение B(n,p)

Случайная величина имеет биномиальное распределение с параметрами n и p, где 0 p1, если принимает значения 0, 1, 2, …n с вероятностями P{ = k} = Cnk pk q n –k.

Случайная величина с таким распределением имеет смысл числа успехов в n испытаниях схемы Бернулли с вероятностью успеха p.