7.3. Инвариантное определение ротора и дивергенции

Определение дивергенции векторного поля связано с выбором системы координат, но пользуясь формулой Гаусса-Остроградского

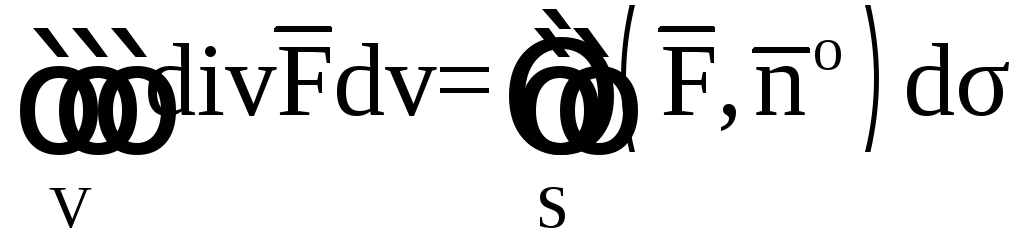(9)

можно дать другое, инвариантное определение дивергенции векторного поля.

Для этого окружим точку M небольшой областью V с объемом v и пусть S есть граница области V.

Применяя (9) и пользуясь теоремой о среднем, запишем

,

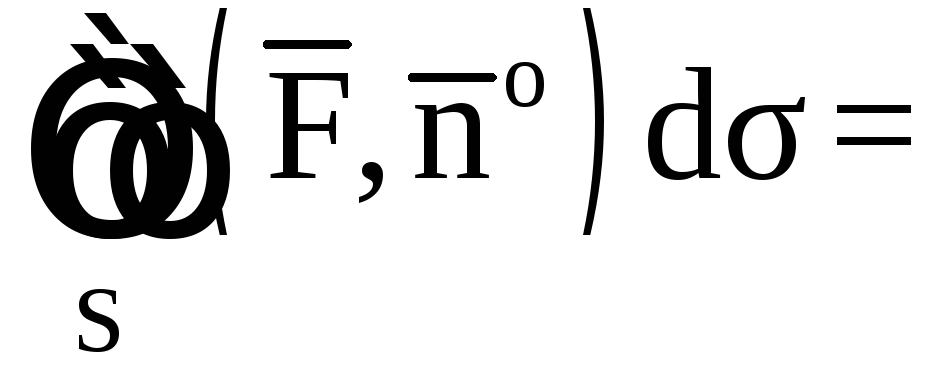
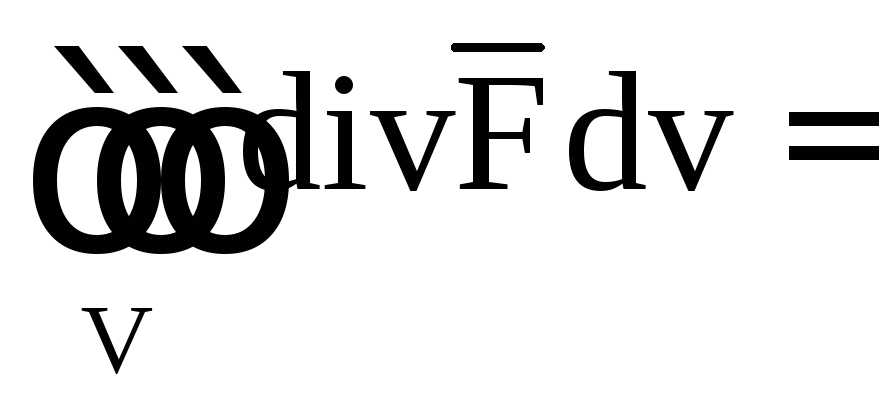
где точка иv – объем области V.

Сжимая V к точке M и учитывая, что тогда , получим

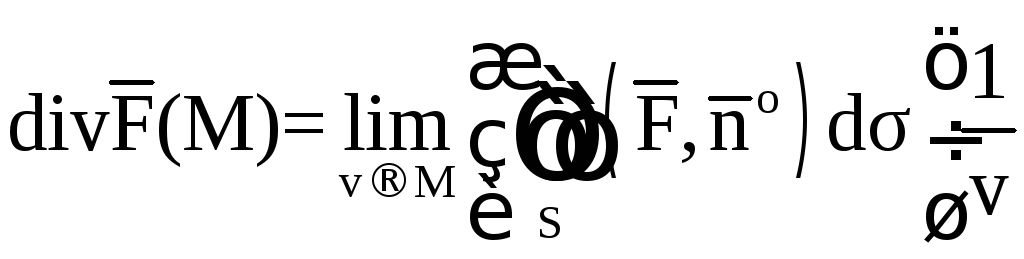. (10)

Аналогично из формулы Стокса получим

,

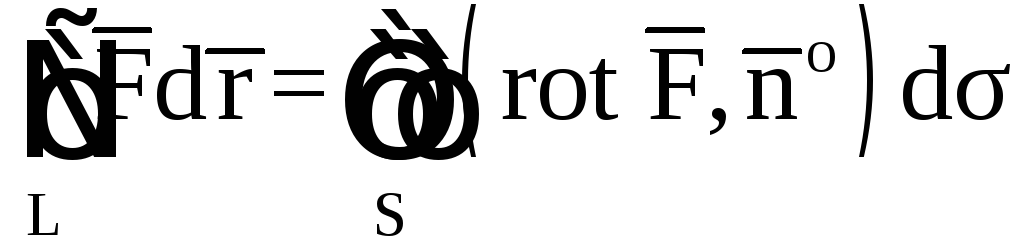где L – граница двумерной области S, а ориентация нормали согласована с ориентацией контураL так, чтобы из конца нормали обход контура в выбранном направлении был виден совершающимся против часовой стрелки, можно получить определение , не связанное с выбором системы координат

.

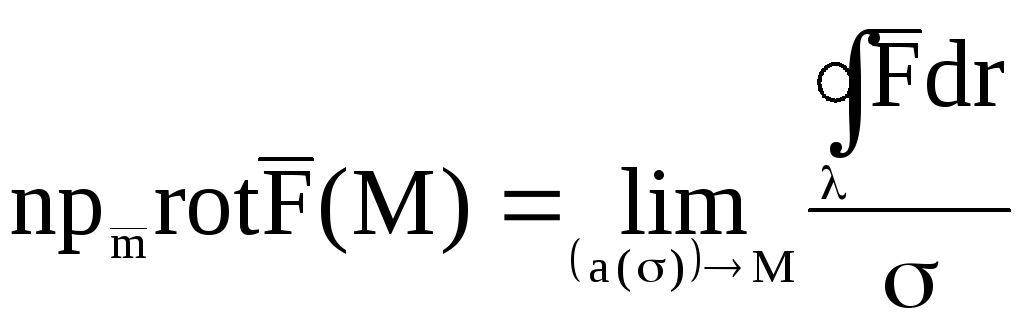Здесь некоторое направление, проходящее через точкуM, −  плоская площадка, проходящая через точкуM перпендикулярно к , σ – площадь областиa(σ), λ – граница области a(σ).

Запись означает, что площадкаa(σ) стягивается к точке M, в которой рассматривается вектор причем направление нормалик этой площадке остается все время одним и тем же.

Пусть скалярное поле u и координаты векторного поля непрерывно дифференцируемые функции. В декартовой системе координат, если

то ,,

.

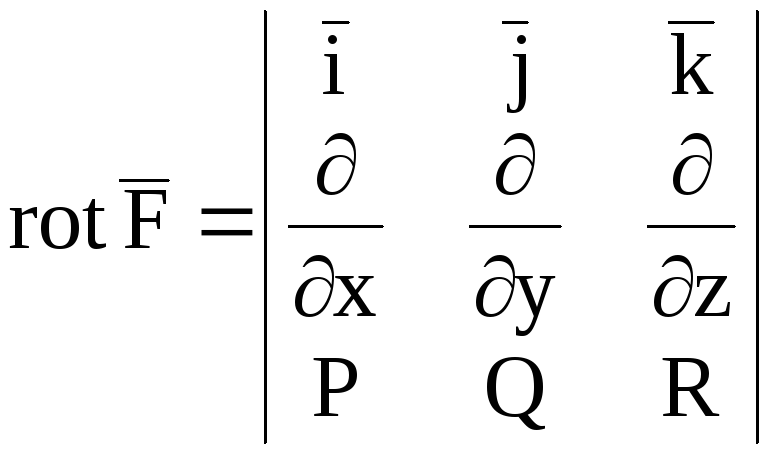Найдем выражения для ,,в криволинейной ортогональной системе координат. Обратимся сначала к.

Рассмотрим элементарный параллелепипед в ортогональных криволинейных координатах и определим поток поля через поверхность этого параллелепипеда.

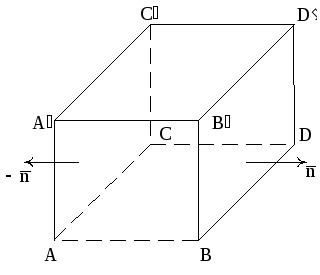
Рис. 18

Далее для вычисления воспользуемся формулой (10).

Начнем с определения потока через правую и левую грани. В основной вершине A криволинейные координаты имеют значения (), остальные вершины имеют следующие координаты:

, ,,

, ,

, .

Заметим, что на правой грани направления внешней нормали совпадают с направлением координатной линииq₁, а на левой грани эти направления противоположны. Еслилокальный ортонормированный базис в точке А, и

, то на правой грани

,

а на левой грани так как из ортонормированности локального базиса следует, что,,.

Ввиду малости граней заменяем поверхностный интеграл по ним просто произведением подынтегральной функциина площадь соответствующей грании таким образом получим для потока через граниивыражение

.

Воспользуемся формулами (8).

Получим

,

где – коэффициенты Ламэ.

По теореме Лагранжа

.

Подставляя это равенство в поверхностный интеграл, получим окончательно выражение потока через правую и левую грани

.

Аналогично поток через заднюю и передние грани

.

А поток через верхнюю и нижние грани

.

Складывая полученные три выражения и деля их на величину элементарного объема (8) , приходим к выражению для дивергенции в криволинейной ортогональной системе координат

.

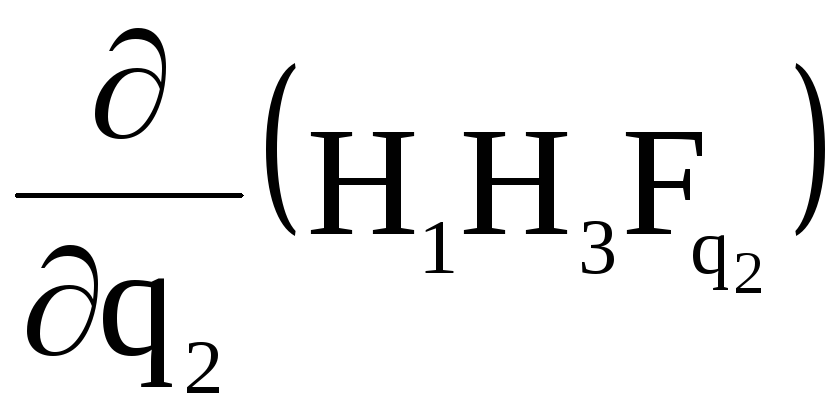
Пусть теперь потенциальное поле,. Разложим векторпо локальному ортонормированному базису в точкеM

.

Тогда, учитывая, что 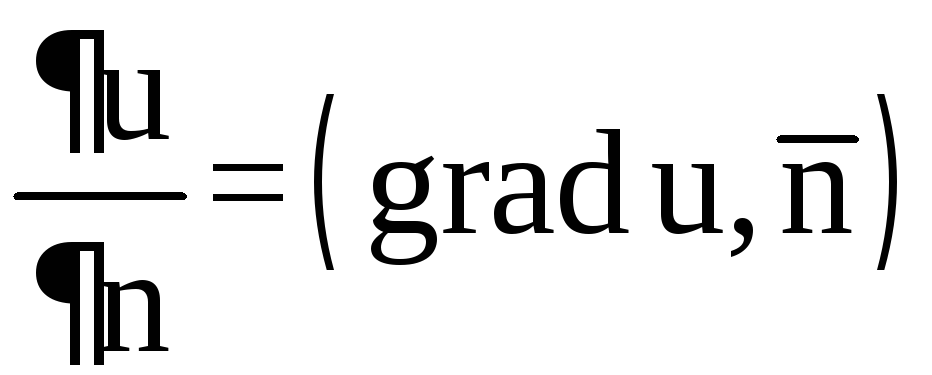[§2], получим

.

Следовательно, есть производная функцииu по направлению .

.

Аналогично ,,

.

Приведем без доказательства выражение для в криволинейной ортогональной системе координат.

Если в локальном базисе

,

то

.

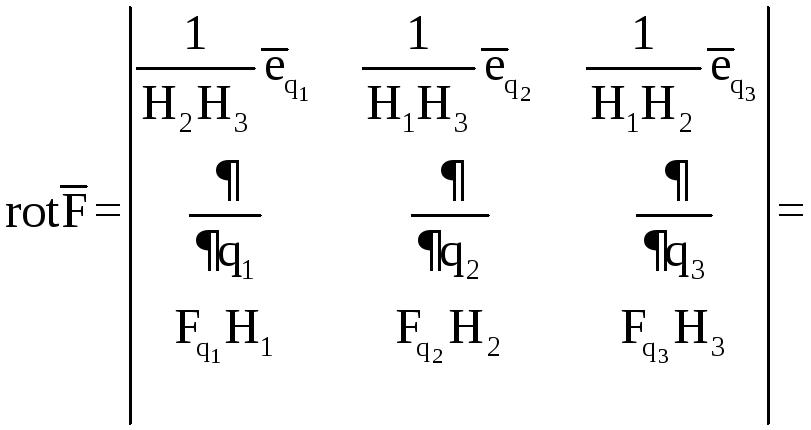
Пусть u – скалярное поле, – ортогональные криволинейные координаты.

Тогда

.

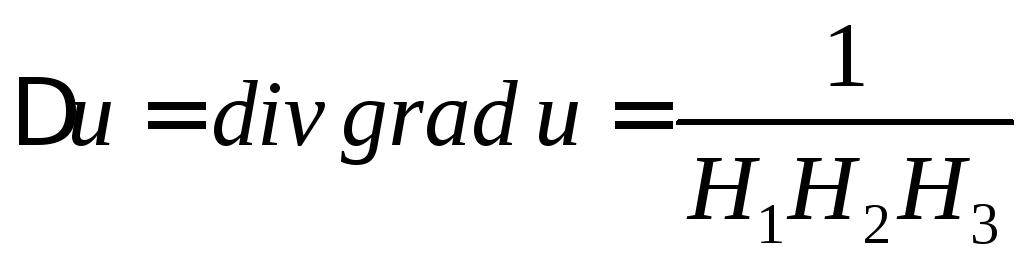
В цилиндрической системе координат () коэффициенты Ламэ

, ,. Если, то

,

,

.

.

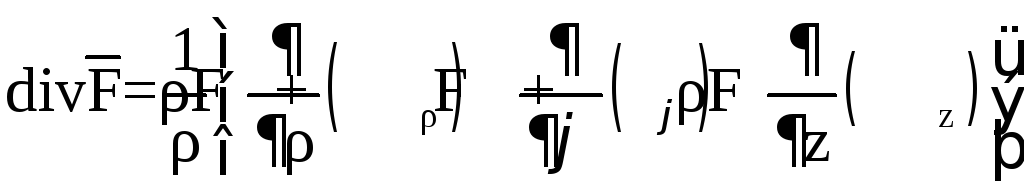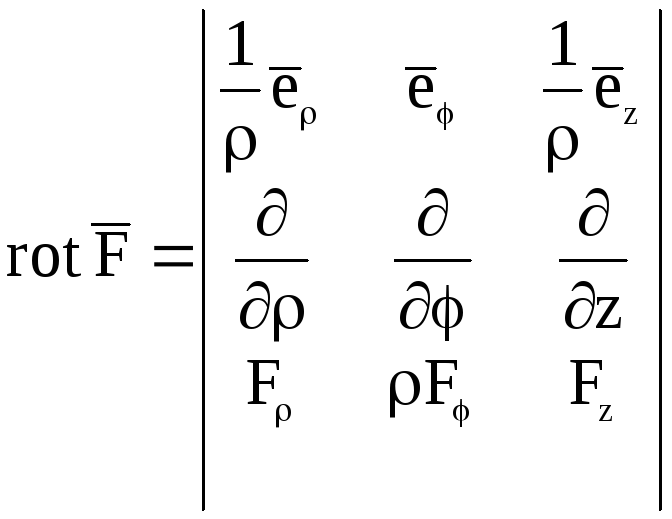В сферической системе координат

; , , .

Если , то

,

,

,

.

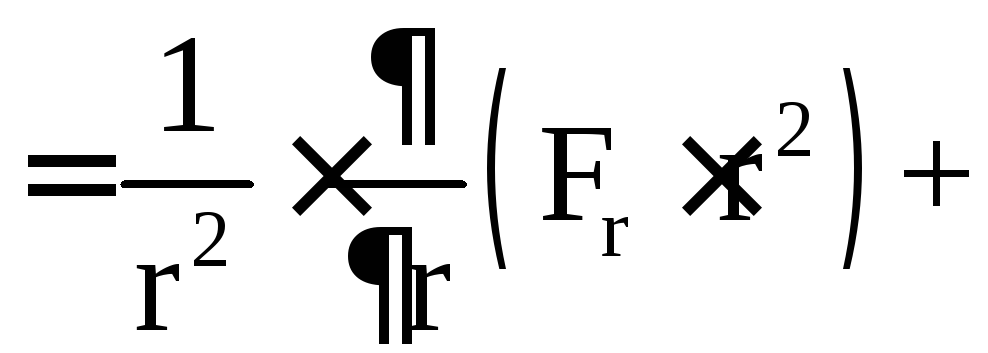
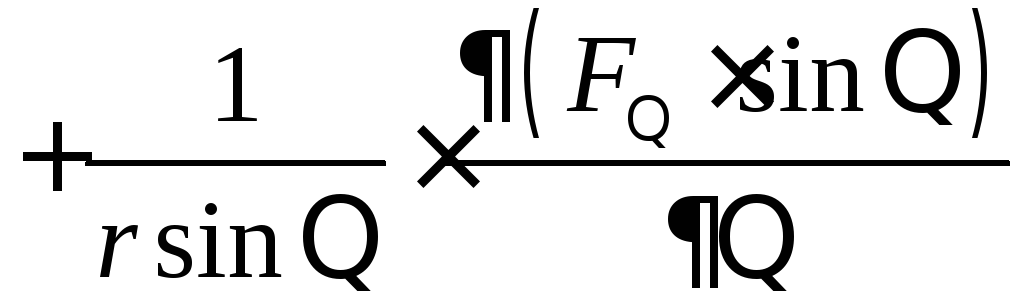
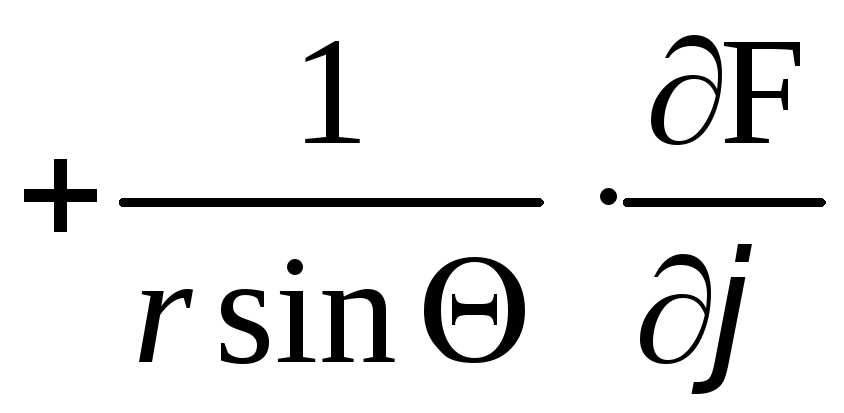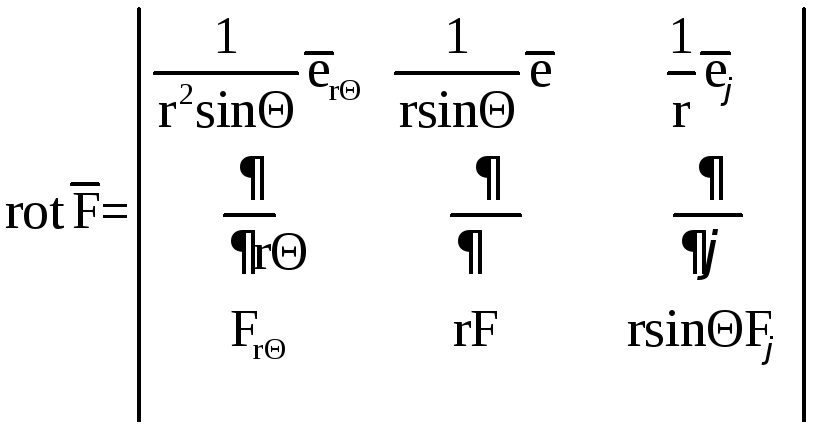Пример 7. Дано векторное поле в цилиндрических координатах. Вычислить,.

Решение. Воспользуемся формулой для дивергенции в цилиндрической системе координат 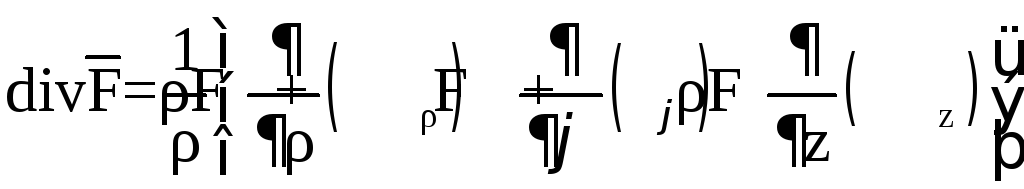.Имеем:

, .

.

.

Далее

.

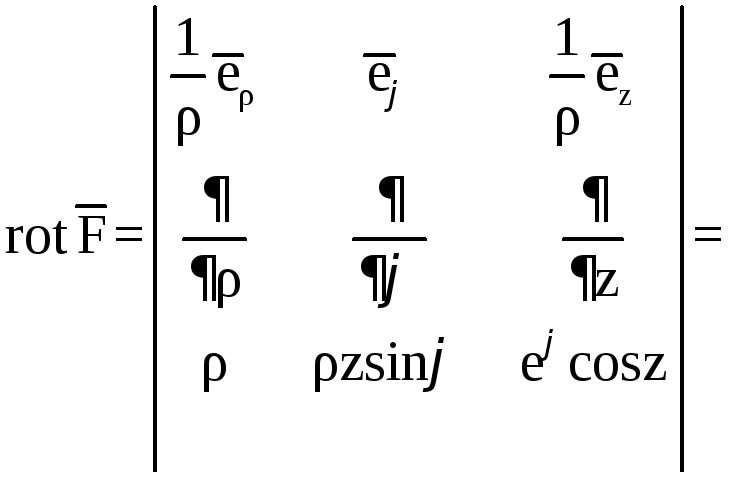
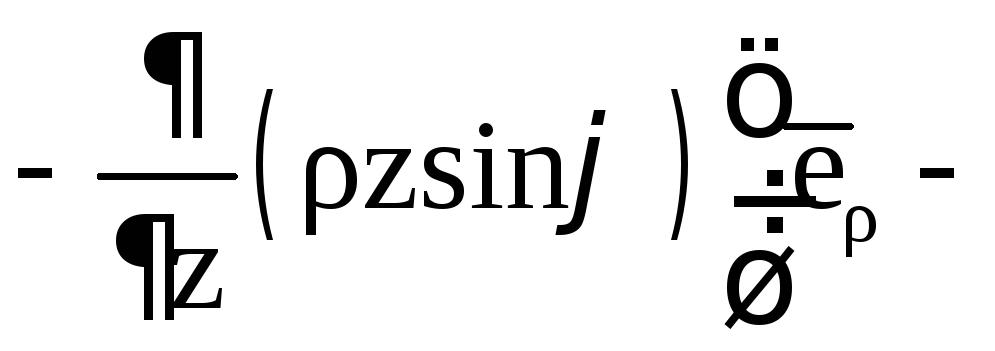
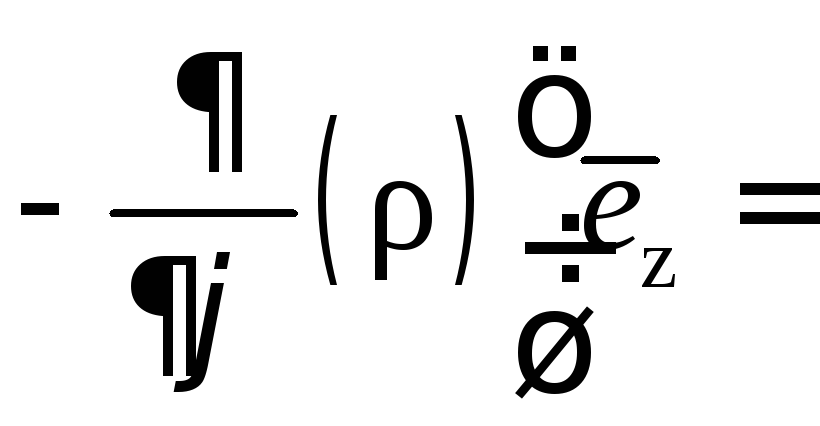
Пример 8. Дано векторное поле

в сферических координатах. Вычислить ,.

Решение. Воспользуемся формулами

.

.

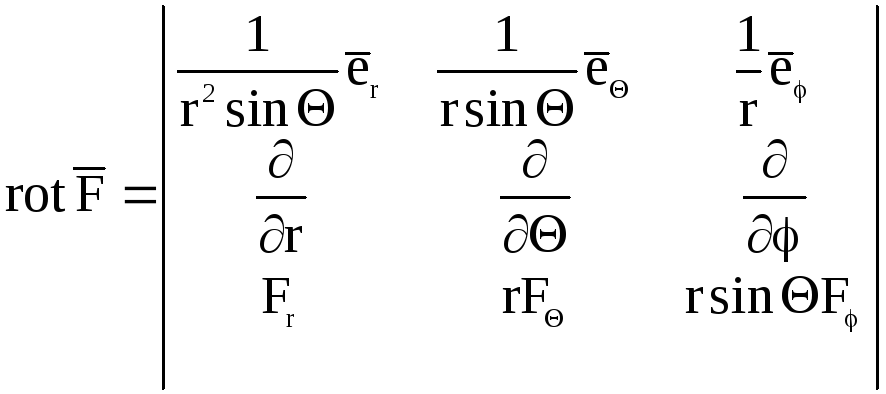Имеем:

;

;

.

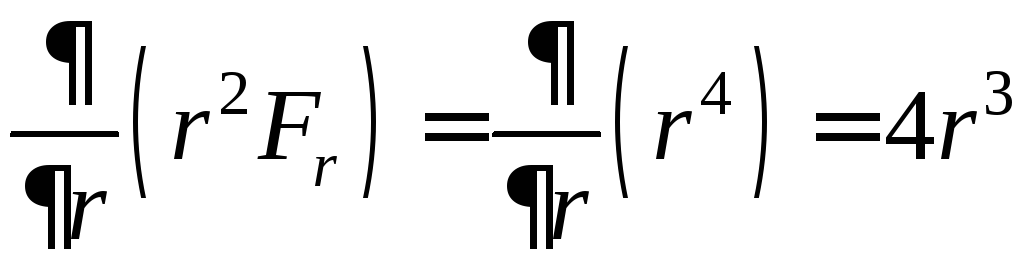
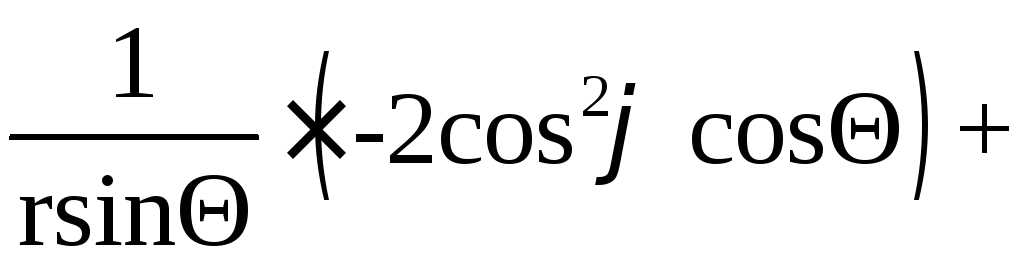
Далее

=;

;

= ;

;

; ; .

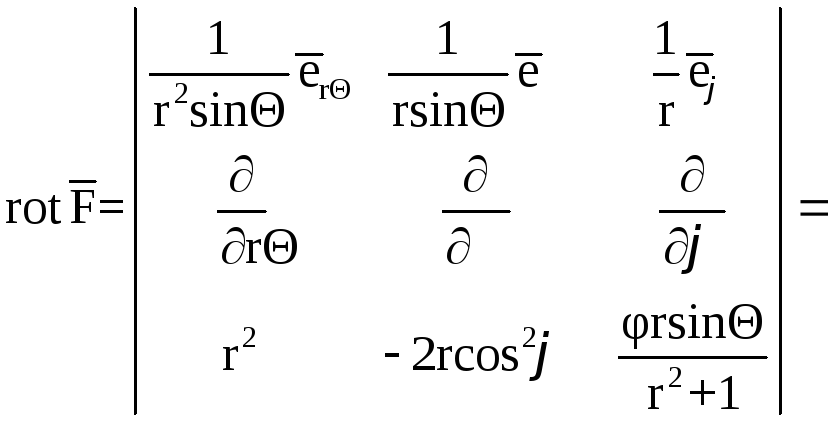
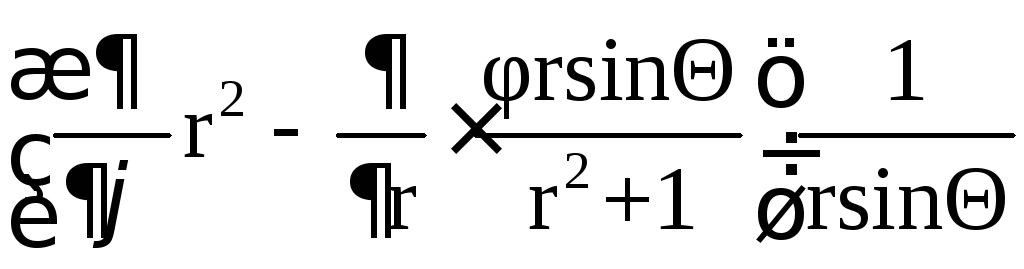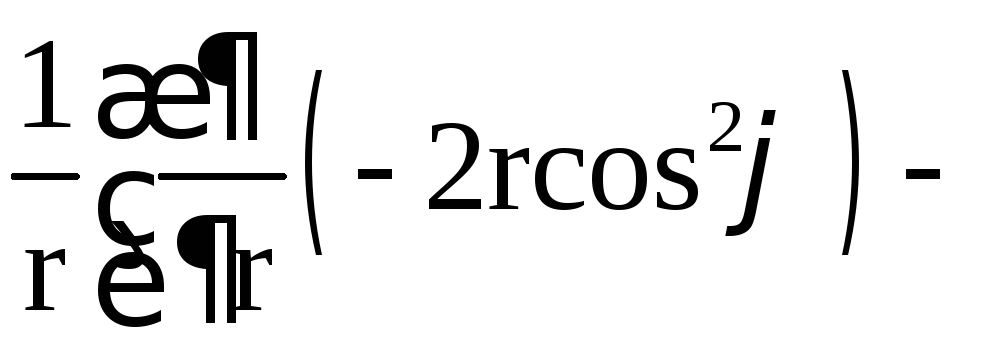
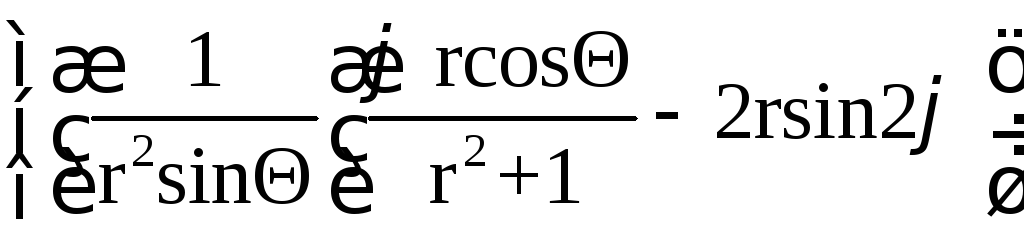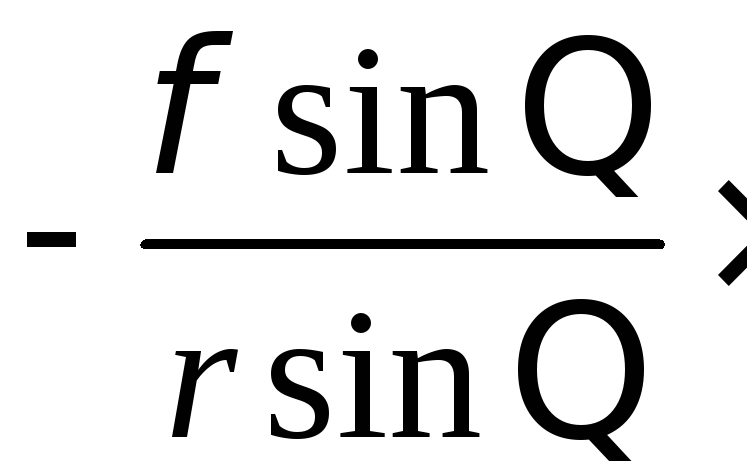
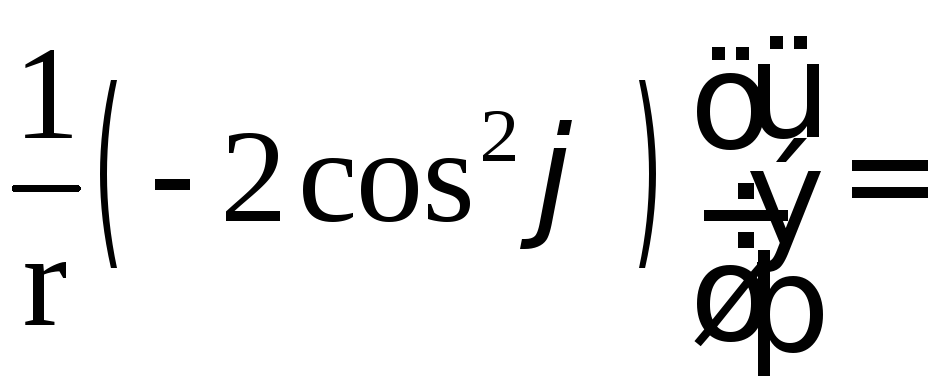
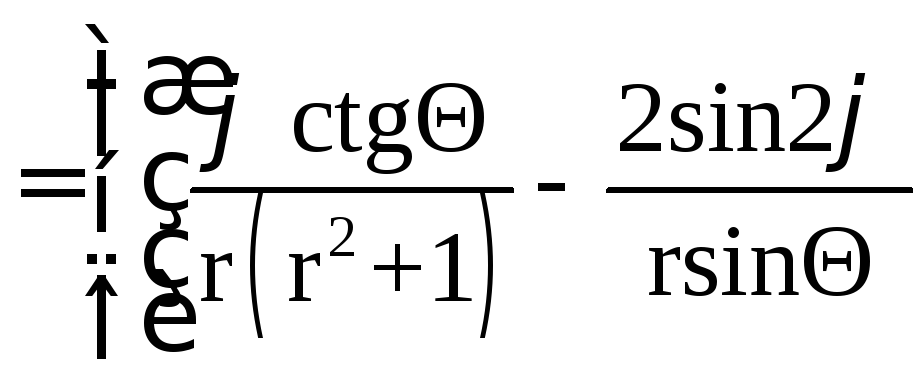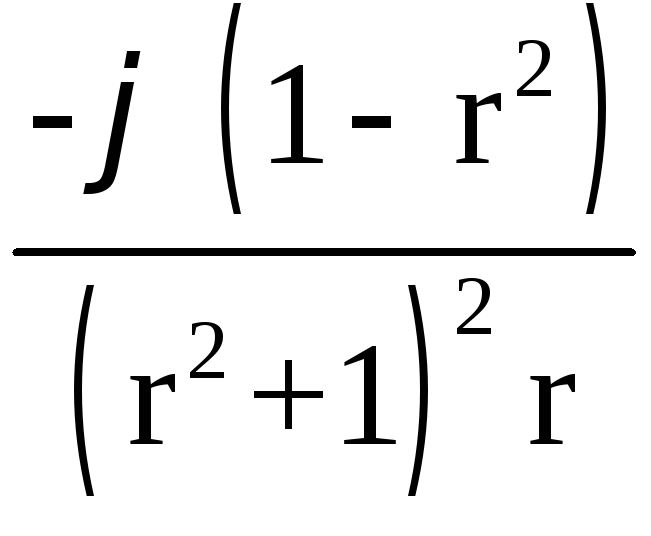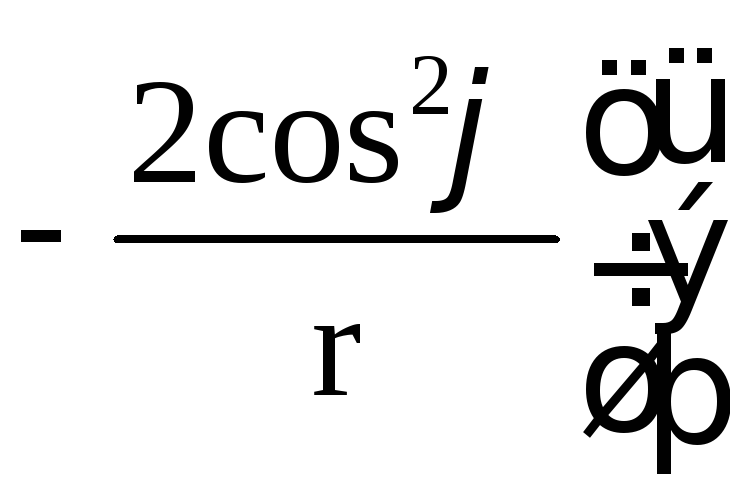Пример 9. Дано скалярное поле в цилиндрических координатах. Найти.

Решение. Оператор Лапласа в цилиндрических координатах имеет вид

.

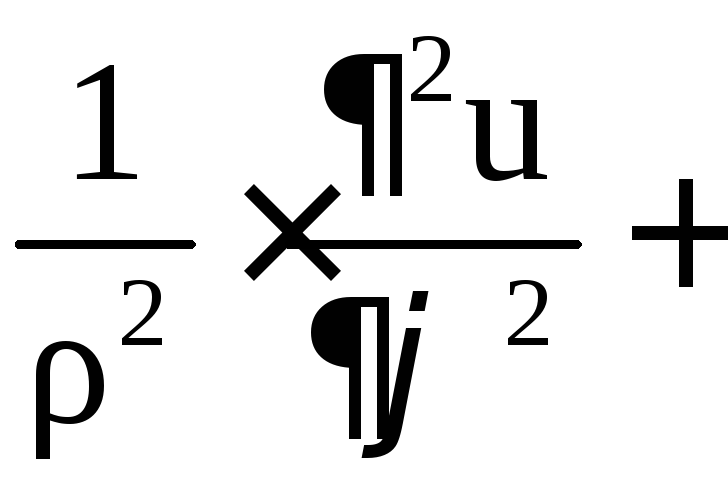
Имеем:

1) , .

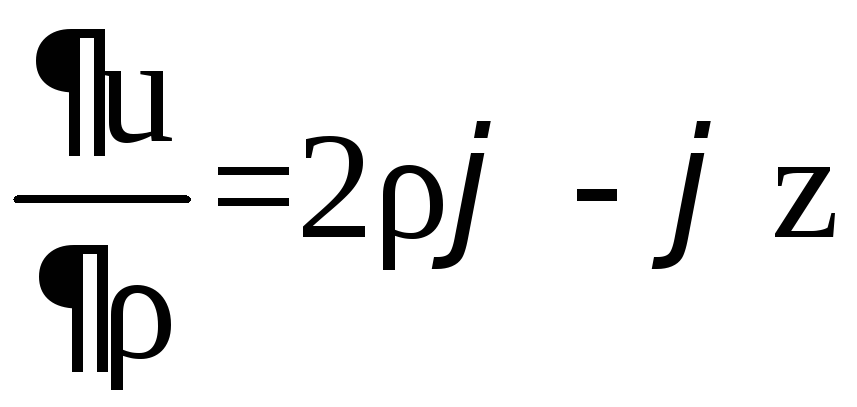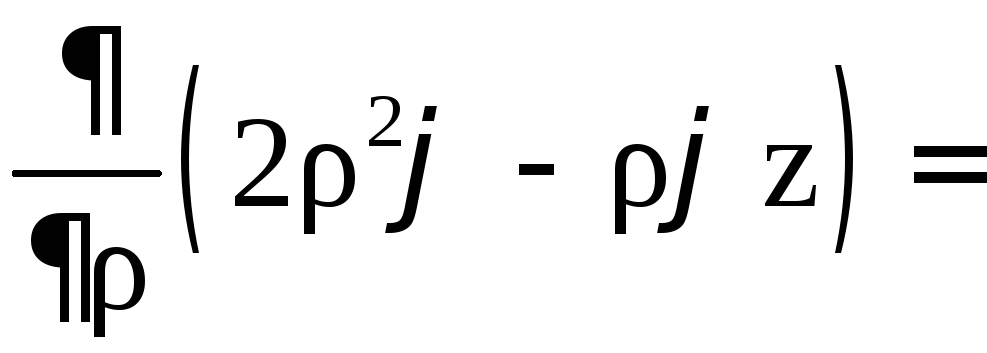
2) ,.

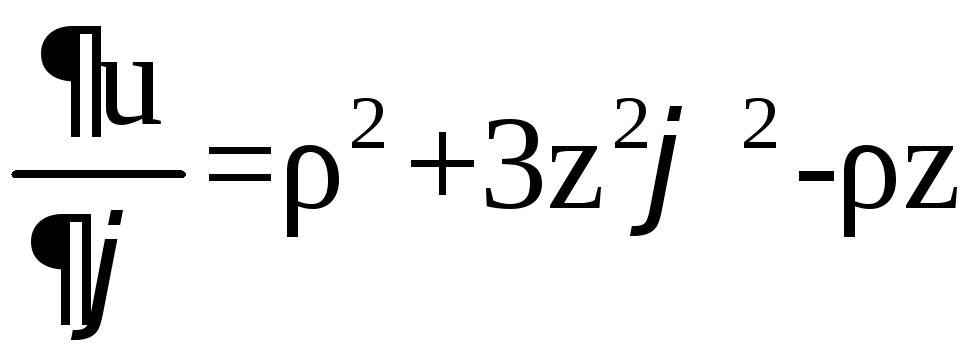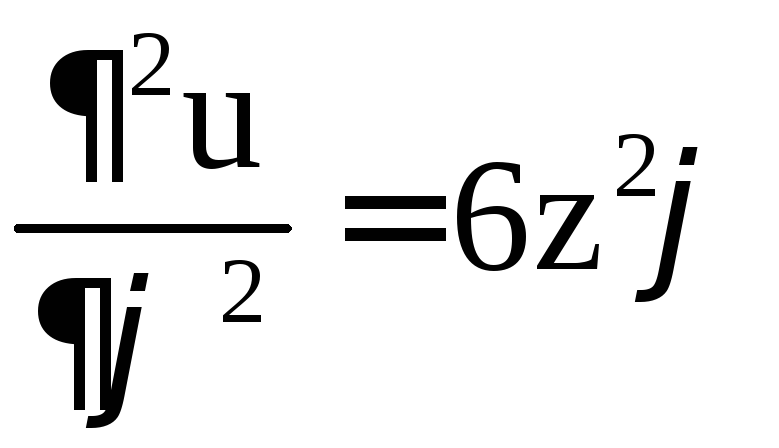3) ,.

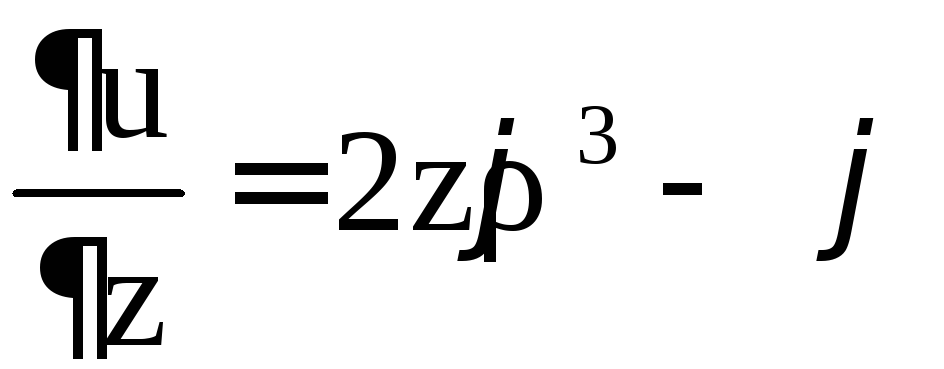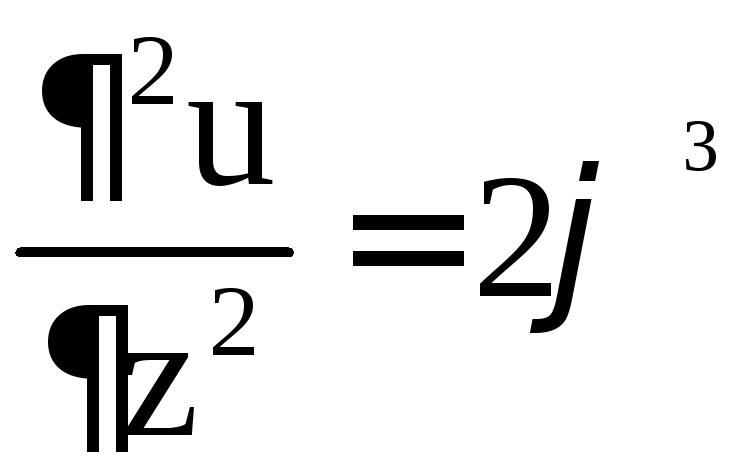4) .

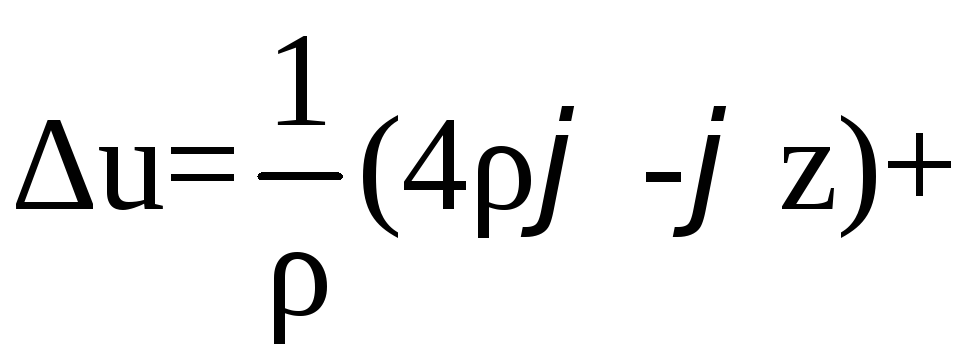
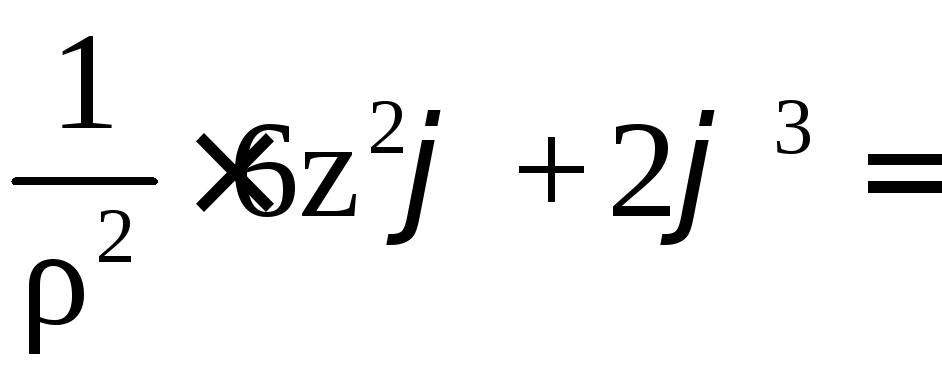
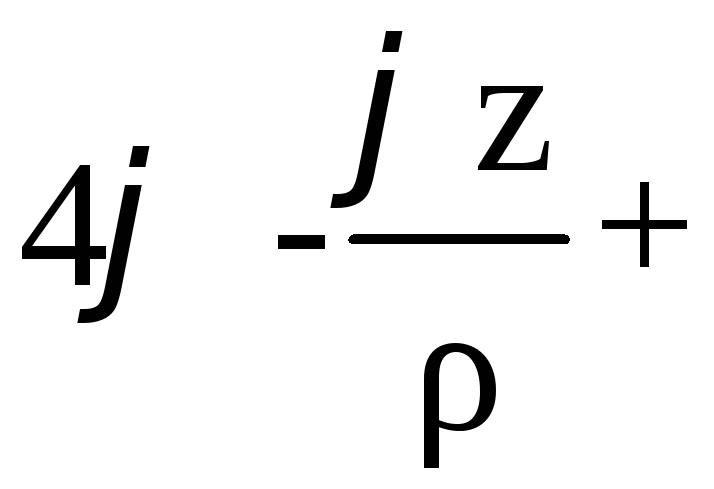
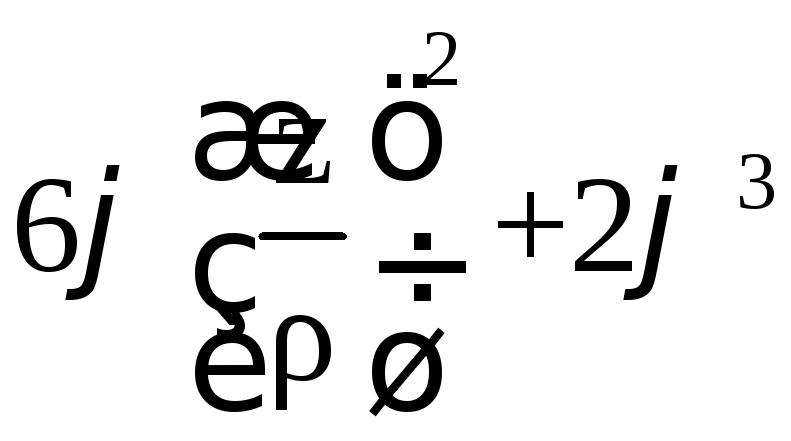Пример 10. Дано скалярное поле

в сферических координатах. Найти .

Решение. Оператор Лапласа в сферических координатах принимает вид

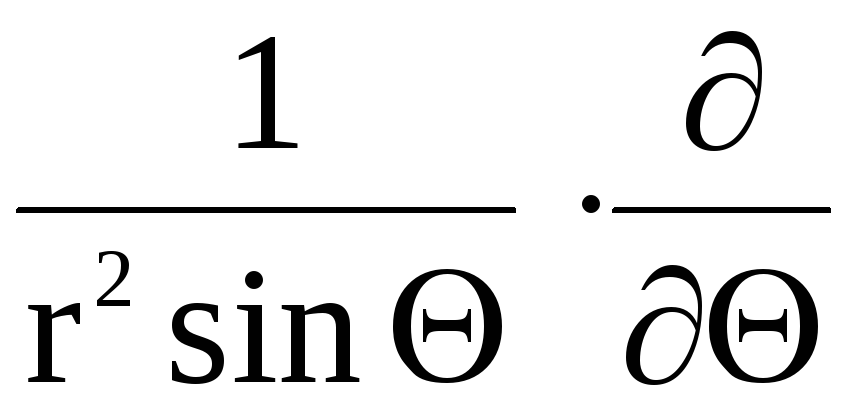
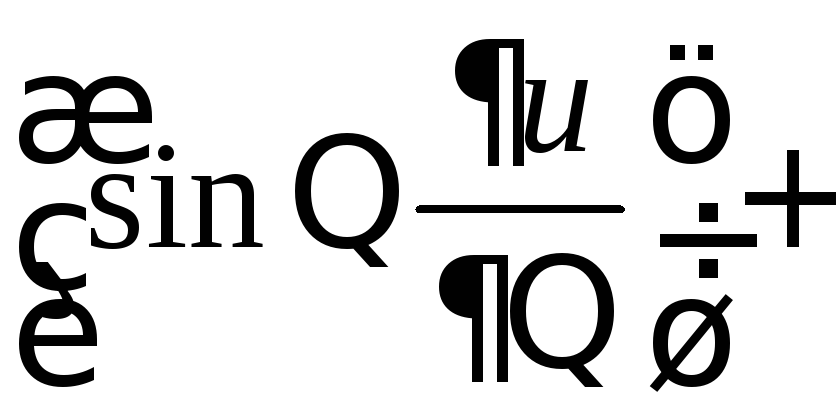
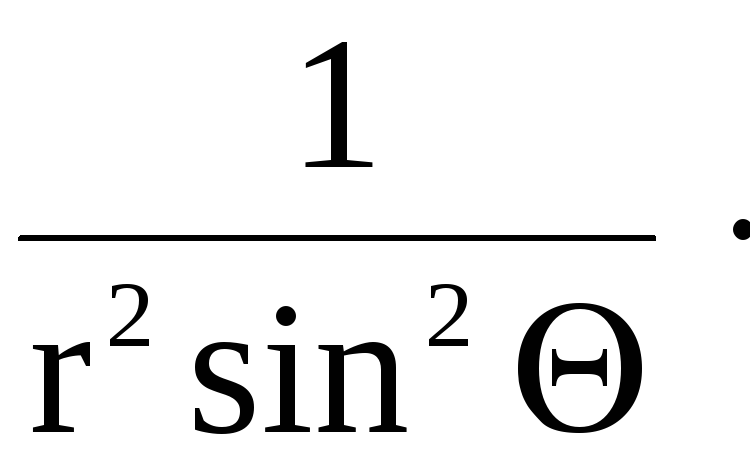
. Имеем:

,

.

.

,   .

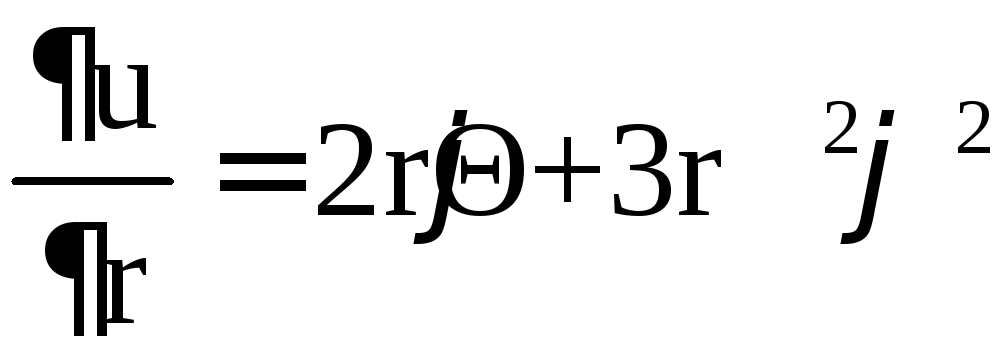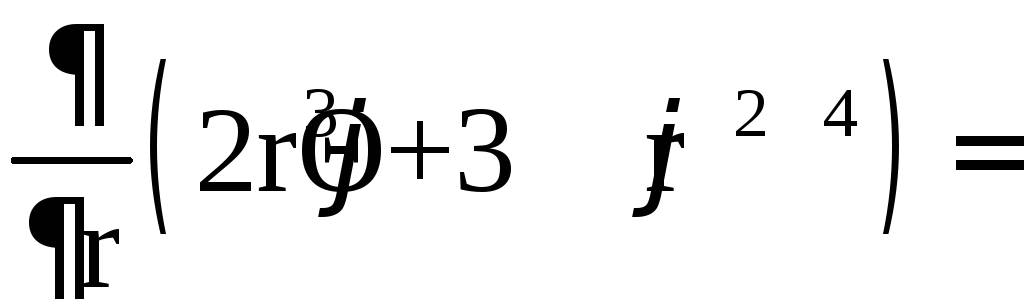
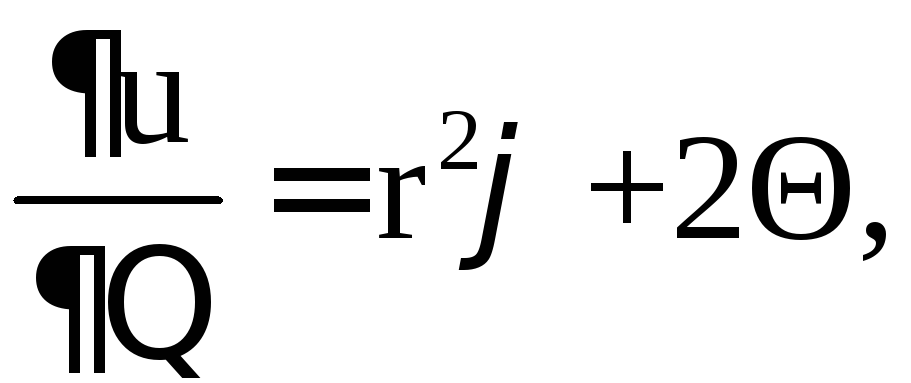
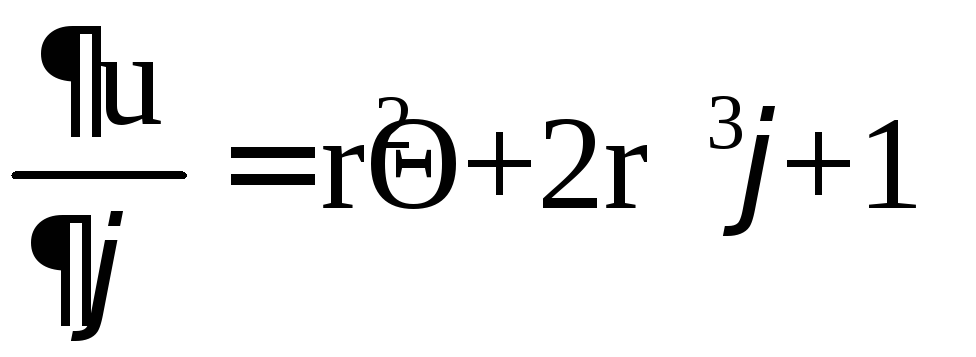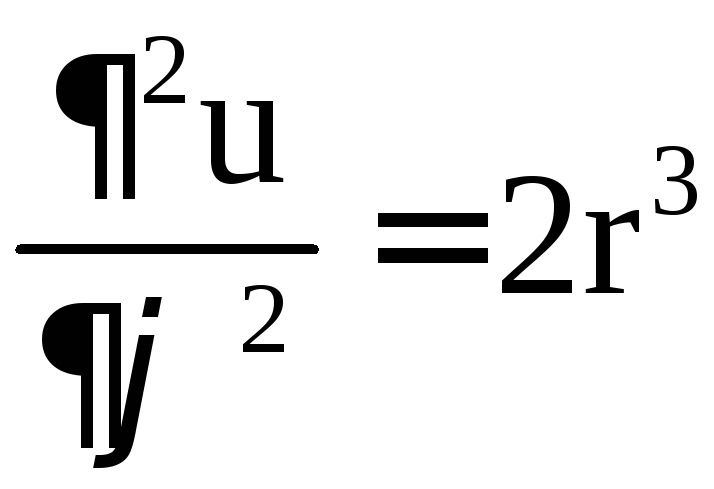Тогда .

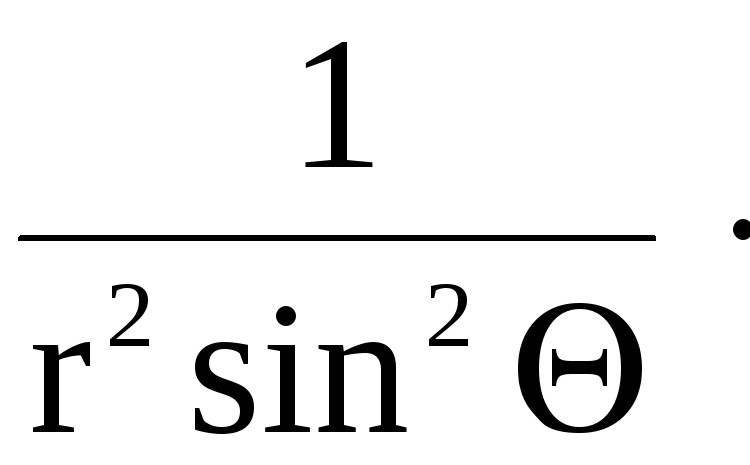
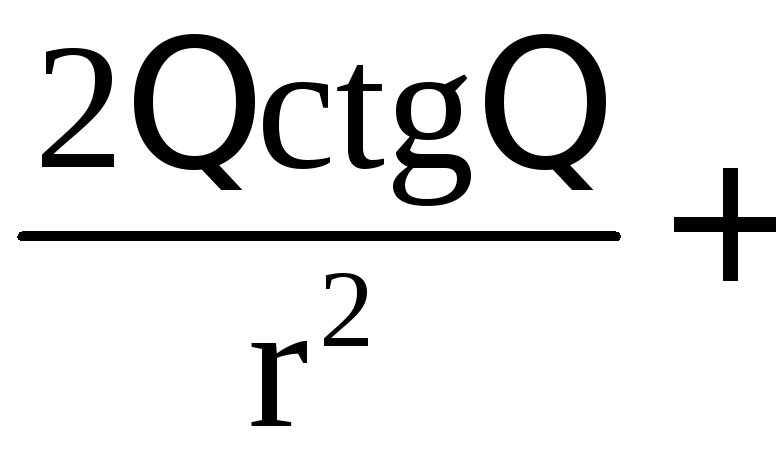
64