3. Криволинейный интеграл II рода. Формула Грина

3.1. Криволинейный интеграл II рода

 Пусть в некоторой области G трехмерного пространства задано непрерывное векторное поле

(это означает, что P,Q,R являются непрерывными функциями трех переменных). И пусть в области G задана направленная (ориентированная) линия L. Разобьем точками на участки, при этом нумерация должна быть согласована с ориентацией линии. Возьмем на каждом участке по точке N_k.

Обозначим .

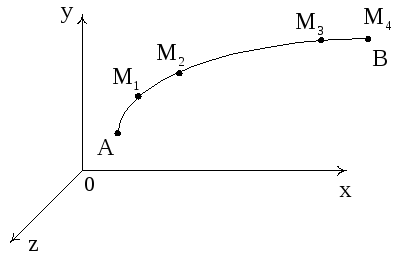
Рис. 3

Рассмотрим сумму скалярных произведений и :

,

называемую интегральной суммой. Предел этой суммы при стремлении к нулю диаметра разбиения называется криволинейным интегралом II рода и обозначается

или .

Если линия задана в параметрической форме (формула 1 §1), то

и криволинейный интеграл запишется в виде

Если задает силовое поле, то криволинейный интеграл II рода дает работу силового поля вдоль линии (АВ).

Отметим некоторые свойства криволинейного интеграла II рода:

а) ;

б) ;

в) .

Если линия (АВ) задана в параметрической форме

, , , ,

то

.

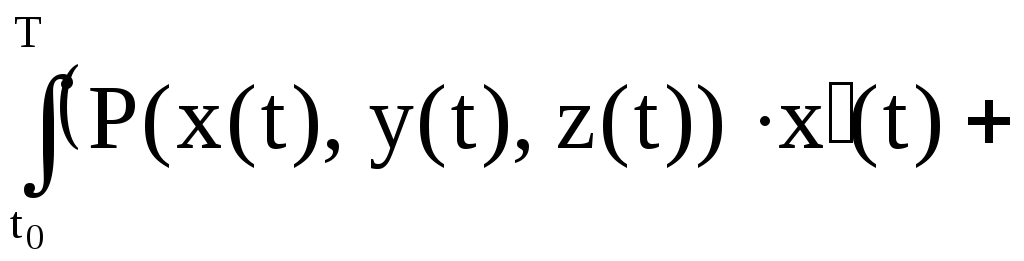
Криволинейный интеграл II рода по ориентированной замкнутой линии (контуру) часто называют циркуляцией.

Пример 1. Вычислить криволинейный интеграл , если

, и (АВ) задана условиями: , , , .

Решение. Имеем , , ,

.

Тогда

.

.

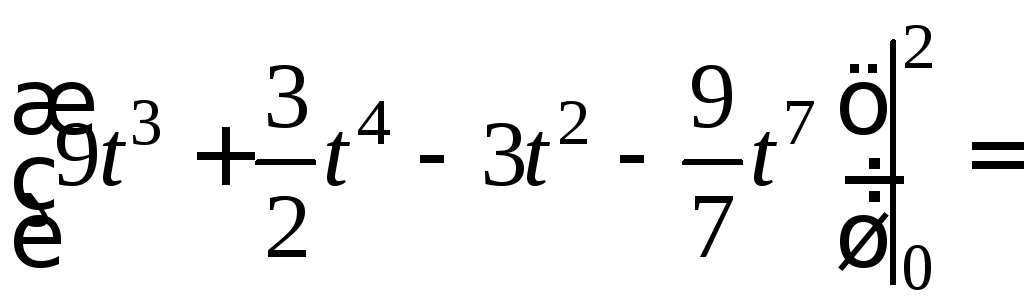
В плоском случае

криволинейный интеграл II рода находится по формуле

.

3.2. Формула Грина

Если в плоской области D, ограниченной линией L, задано векторное поле , гдеP и Q имеют непрерывные частные производные, то имеет место формула Грина:

.

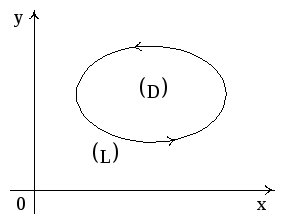
Рис. 4

При этом L считается ориентированной в положительном направлении, то есть обход вдоль L осуществляется так, чтобы область D оставалась слева.

Эта формула справедлива не только для односвязных областей (как на рисунке), но и для многосвязных областей, границы которых состоят из нескольких компонент (например, кольцо). Формула Грина позволяет свести циркуляцию к двойному интегралу.

Пример 2. Вычислить криволинейный интеграл

,

где L – треугольник, заданный условиями: иориентированный в положительном направлении.

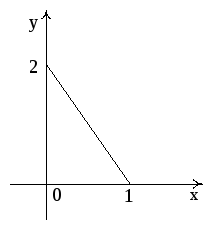
Рис. 5

Решение.

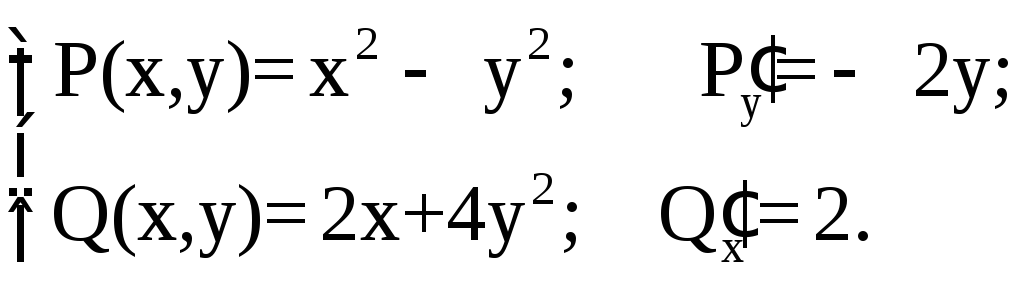
Воспользуемся формулой Грина. Тогда наш интеграл будет равен (D – треугольник) двойному интегралу

.

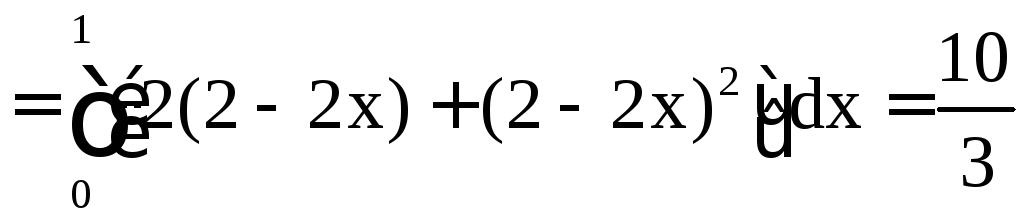4. Поток векторного поля. Теоремы Гаусса-Остроградского и Стокса

4.1. Поток векторного поля

Пусть имеем векторное поле

,

координаты которого P,Q,R – непрерывны в некоторой области G трёхмерного пространства. Пусть в G задана гладкая или кусочно-гладкая ориентируемая поверхность S.

Определение. Потоком П векторного поля через ориентируемую поверхностьS называется

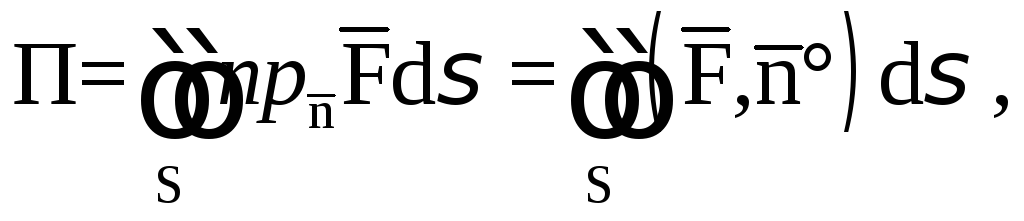
где единичный вектор нормалик выбранной стороне поверхностиS;

–элемент площади поверхности S.

В случае замкнутой поверхности будем всегда выбирать внешнюю нормаль , которая направлена наружу области, ограниченной поверхностьюS.

Если углы, которые образует с осями координатOX, OY, OZ нормаль к поверхностиS, то

,

где ,,

Основные свойства потока векторного поля

a) ,

где S⁺ – сторона поверхности S, на которой выбрана нормаль , а – сторона поверхности S, на которой берется нормаль .

б) ,

где числа, векторное поле.

в) Если поверхность S состоит из нескольких гладких частей , которые могут пересекаться разве что по своим границам, то

.

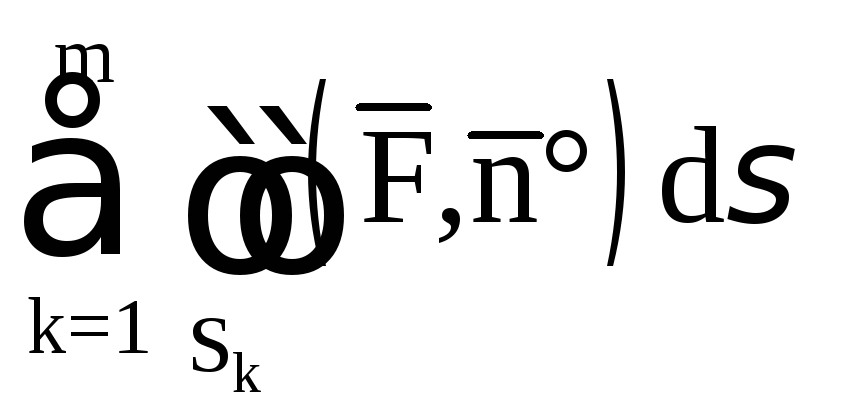Пример 1. Найти поток векторного поля

через площадку, перпендикулярную оси OY, имеющую форму прямоугольника со сторонами, равными 1 и 2 в положительном направлении оси OY.

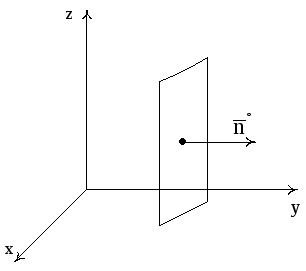
Рис. 6

Решение. В нашем случае

, .

.

Пример 2. Найти поток векторного поля 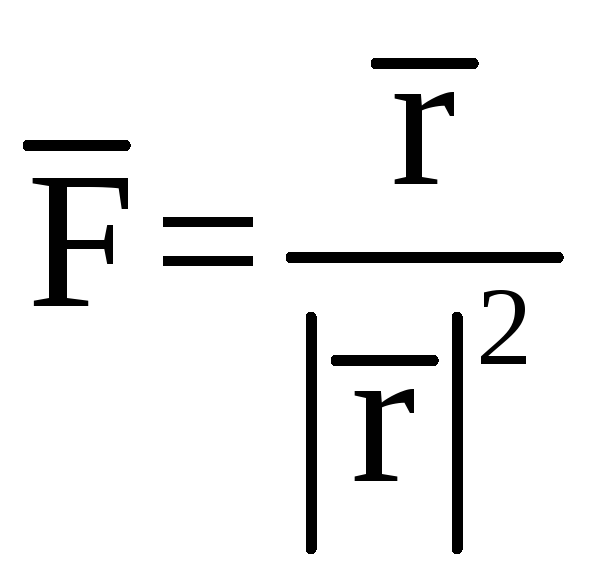через сферу радиусаR с центром в начале координат. Здесь радиус-вектор точки.

Решение. Так как нормаль к сфере коллинеарная вектору , то

.

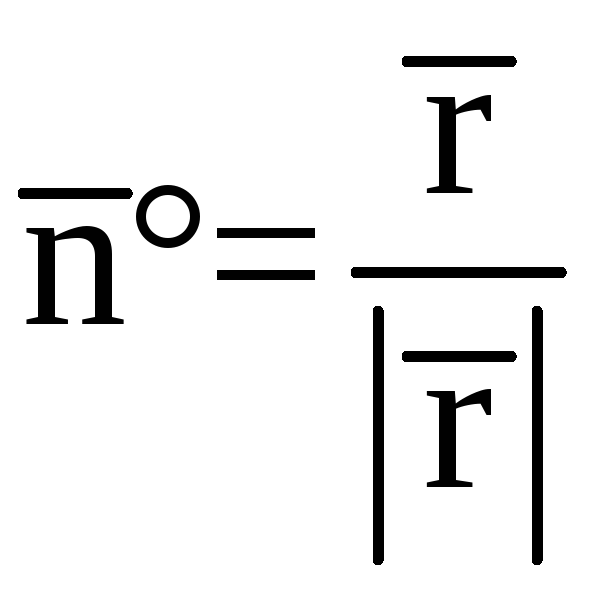Поэтому

На сфере S , поэтому;

.

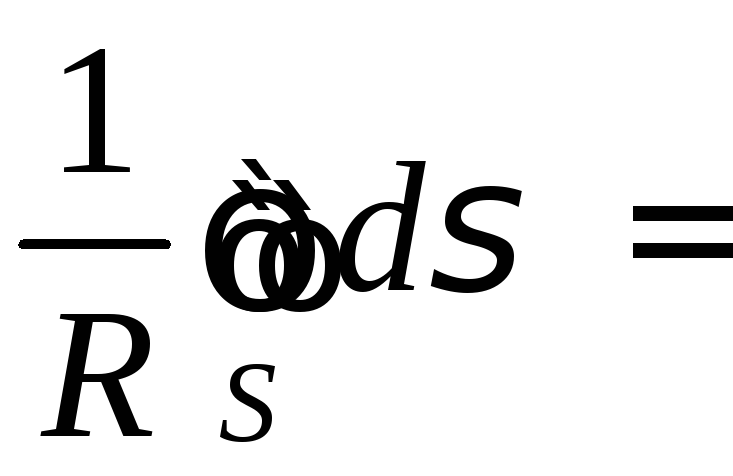
Пусть незамкнутая поверхность S взаимно − однозначно проектируется на плоскость XOY в область D_xy. В этом случае поверхность S можно задать уравнением и поток П вычисляется по формуле

.

Здесь орт нормали к выбранной стороне поверхностиS находится по формуле (4) §1.

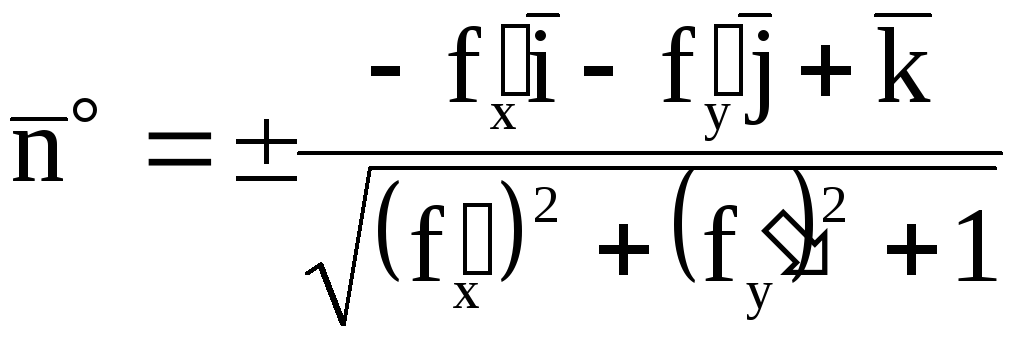, (1)

а . (2)

Если угол γ между осью OZ и острый, то в формулах (1), (2) берется знак «+», если же уголγ тупой, то берется знак «–».

Символ означает, что в подынтегральной функции вместоz надо подставить f(x,y).

Если поверхность S взаимно − однозначно проектируется в область D_yz плоскости Y0Z, а значит, ее можно задать уравнением , то

,

где

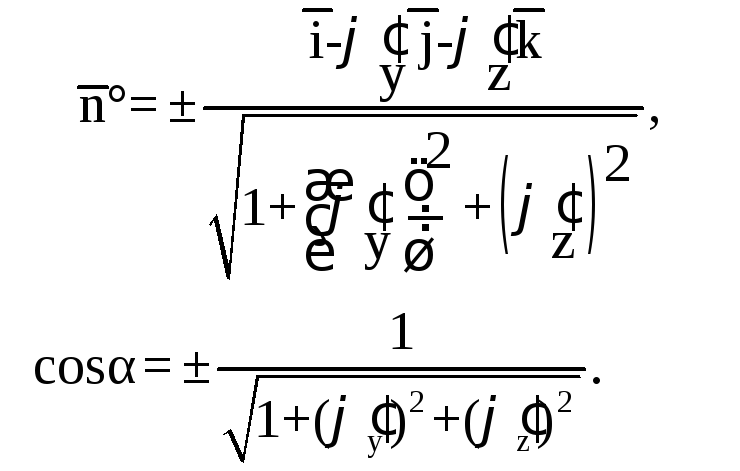
Знак «+» берется в случае, если угол α между осью OX и нормалью острый, если же α – тупой угол, то берут знак «–». Если поверхностьS взаимно − однозначно проектируется в область D_xz плоскости XОZ, а значит ее можно задать уравнением , тогда

dxdz,

где , .

Если угол β между осью 0Y и острый, то берут знак «+», если же угол β – тупой, то берут знак «–».