4.2. Теорема Гаусса-Остроградского

Если в некоторой области G пространства координаты вектора непрерывны и имеют непрерывные частные производныето

.

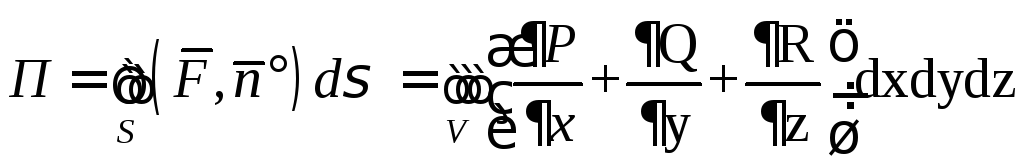
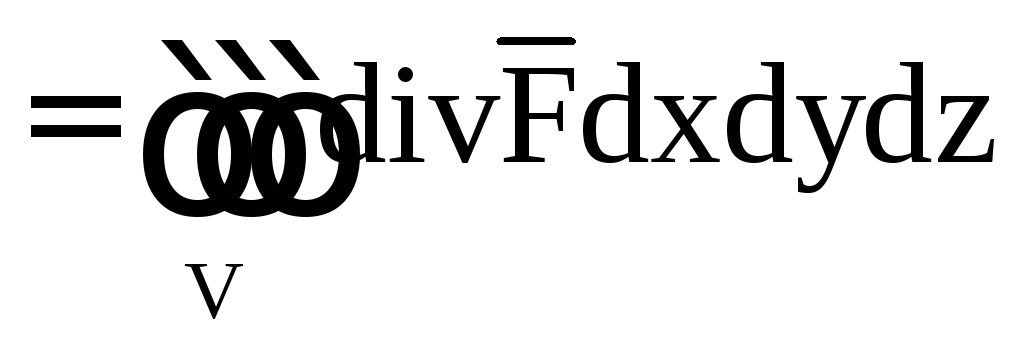Здесь область ограничена кусочно-гладкой поверхностьюS, нормаль к поверхностиS берется внешняя.

4.3. Теорема Стокса

Пусть координаты вектора

непрерывны и имеют непрерывные частные производные. Тогда циркуляция вектора по замкнутому контуруL равна потоку ротора этого вектора через любую поверхность S, натянутую на контур L

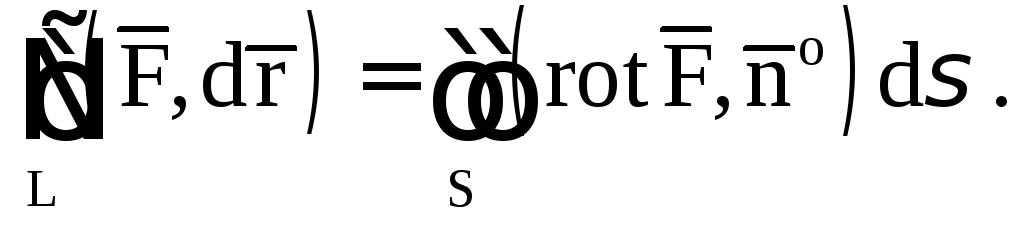
Предполагается, что ориентация нормали к поверхностиS согласована с ориентацией контура L так, чтобы из конца нормали обход контура в выбранном направлении был виден совершающимся против часовой стрелки.

Пример 3. Даны: векторное поле и плоскость(P), которая совместно с координатными плоскостями образует пирамиду V. Обозначим основание пирамиды, принадлежащее плоскости (P), через σ₁; ограничивающий σ₁ контур – через L; нормаль к σ₁, направленную вне пирамиды V – через .

Требуется вычислить:

1) поток векторного поля через поверхность σ₁ в направлении нормали ;

2) поток векторного поля через полную поверхность σ пирамидыV в направлении внешней нормали к ее поверхности σ непосредственно и, применив теорему Остроградского;

3) циркуляцию векторного поля по замкнутому контуруL непосредственно и, применив теорему Стокса к контуру L и ограниченной им поверхности σ₁ с нормалью .

Решение. Сделаем чертеж. Для этого преобразуем уравнение плоскости к виду

.

Из этого уравнения следует, что плоскость отсекает на осях 0X, 0Y, 0Z соответственно отрезки ,(рис. 7).

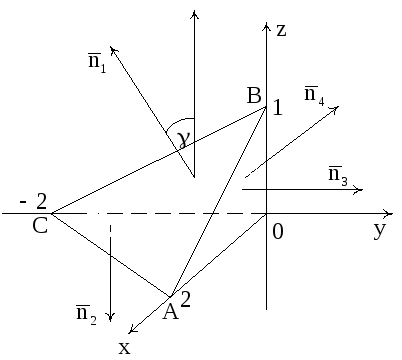
Рис. 7

Эта и координатные плоскости образуют пирамиду V с основанием σ₁ (∆ АВС), а ограничивающий σ₁ контур обозначен через L.

1. Вычислим поток векторного поля через поверхность σ₁ в направлении нормали .

Спроектируем поверхность σ₁ на плоскость X0Y в область D_xy.

Поток найдем по формуле

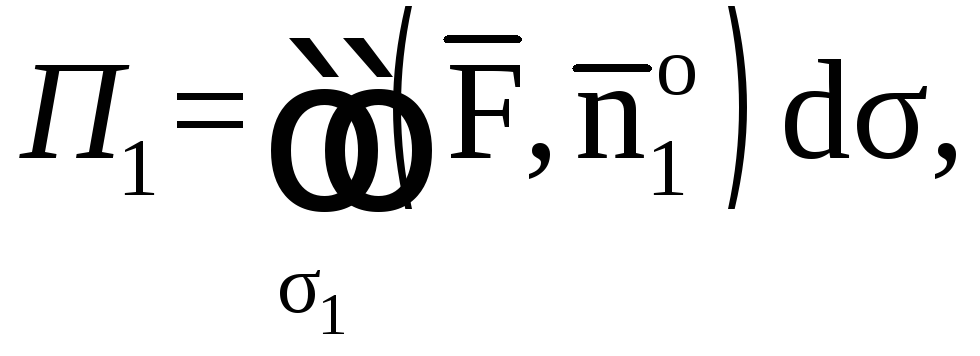
где единичный вектор нормалинаправленный вне пирамиды (рис.7). По условию нормаль к плоскостиимеет координаты.

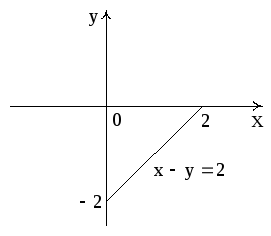
Рис. 8

Тогда

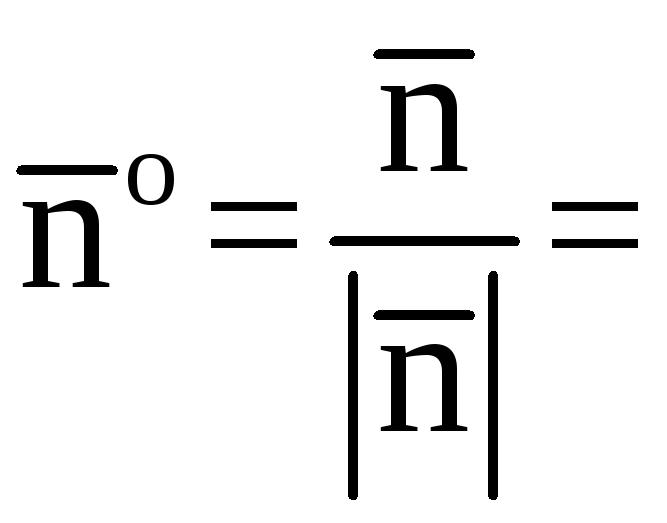
Так как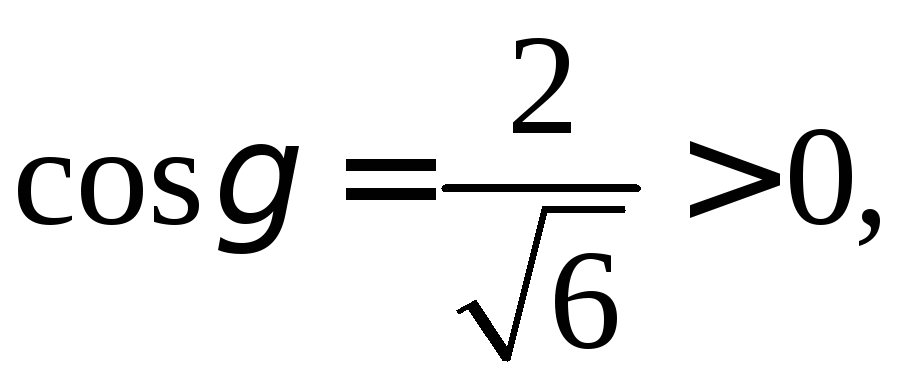то уголγ между осью OZ и острый, нормальнаправлена вне пирамиды, что соответствует выбранной стороне поверхности. Следовательно, в качестве векторавозьмём вектор

Если , то в качестве векторанеобходимо взять вектор.

Элемент площади .

Итак,

.

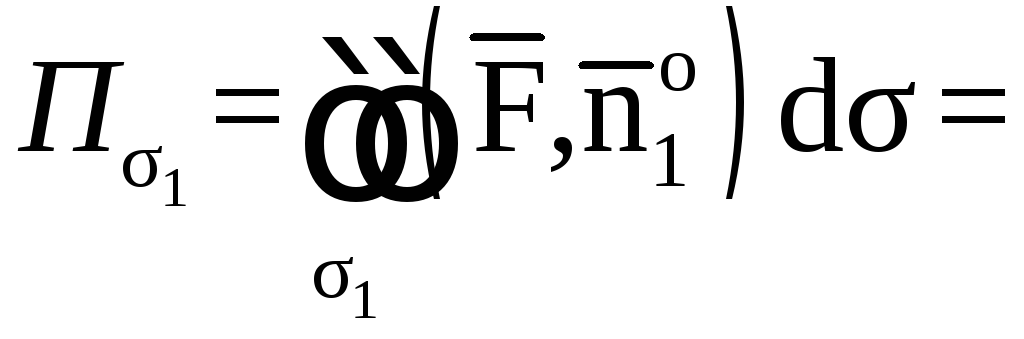
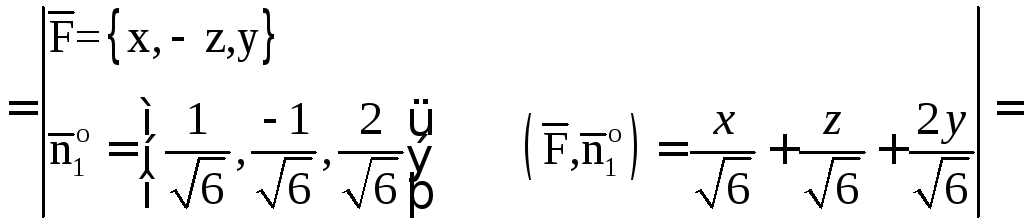
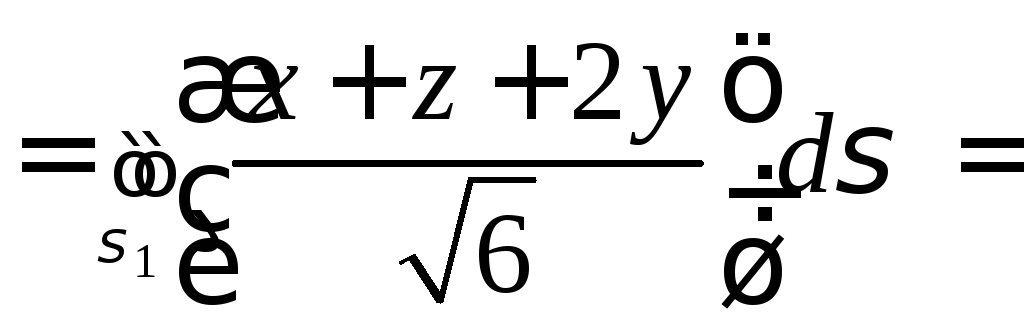
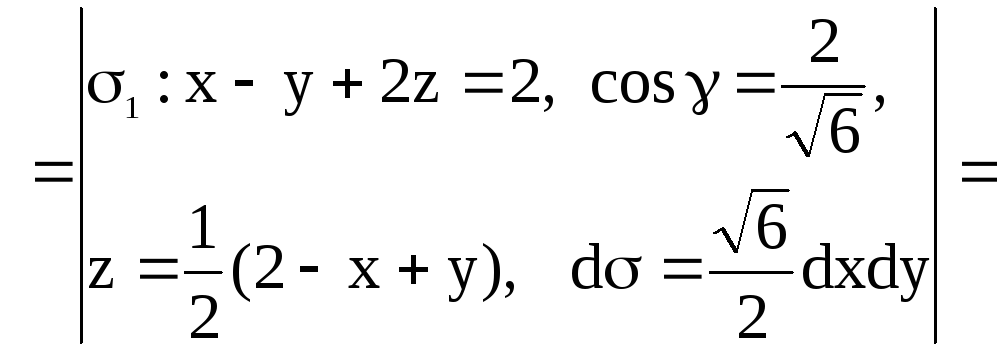
2. Вычислим поток векторного поля через полную поверхностьпирамидыV в направлении внешней нормали к ее поверхности непосредственно.

,

где ,,,

.

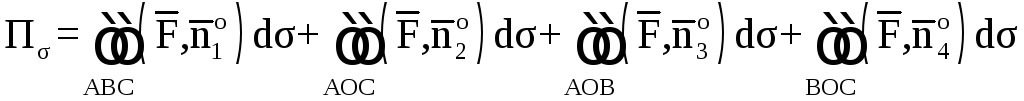Вычислим каждый поверхностный интеграл

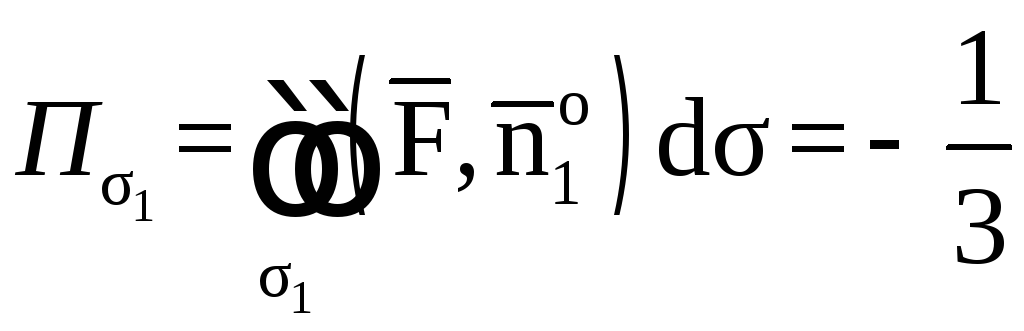уже найден.

На гранях АОС, АОВ, ВОС, соответственно , а единичные векторы внешней нормали к этим граням соответственно равны

.

Заметим, что уравнение прямой АС можно получить как пересечение плоскости АВС и плоскости ХОУ: z = 0; АС: х у = 2; Аналогично уравнение прямой АВ:x+2z=2. Уравнение прямой ВС:

y+2z = 2.

Поэтому будем иметь:

;

;

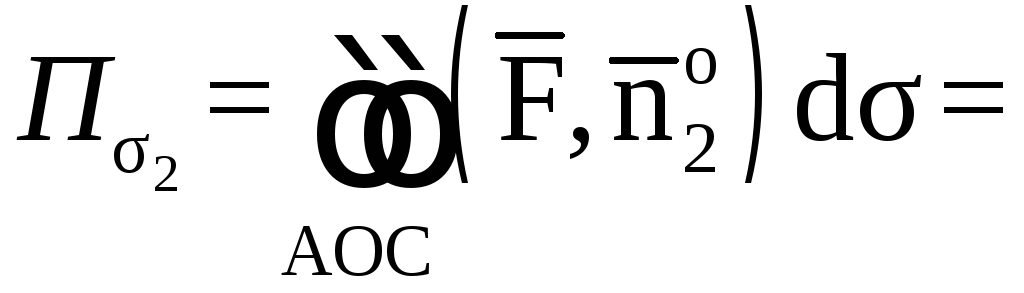
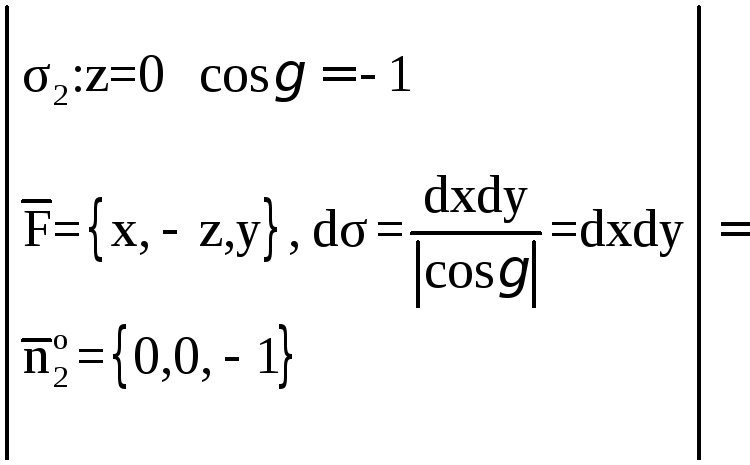
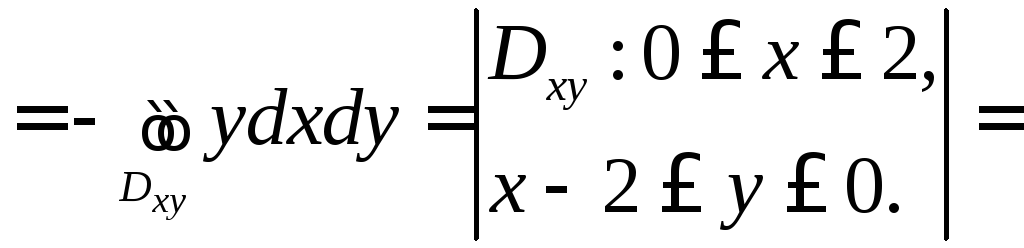
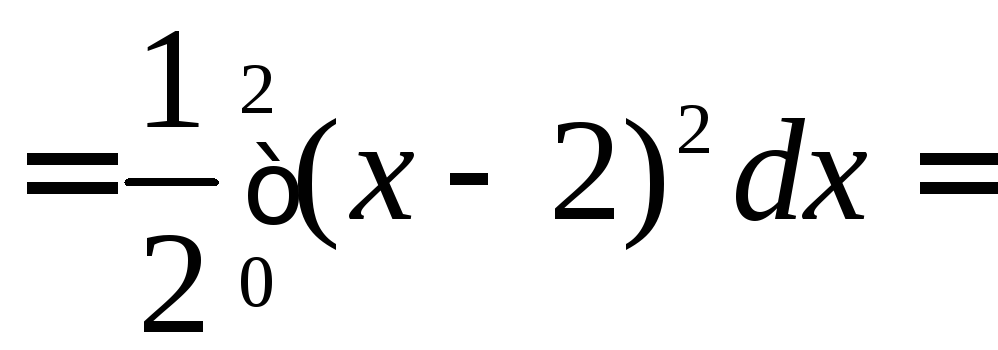
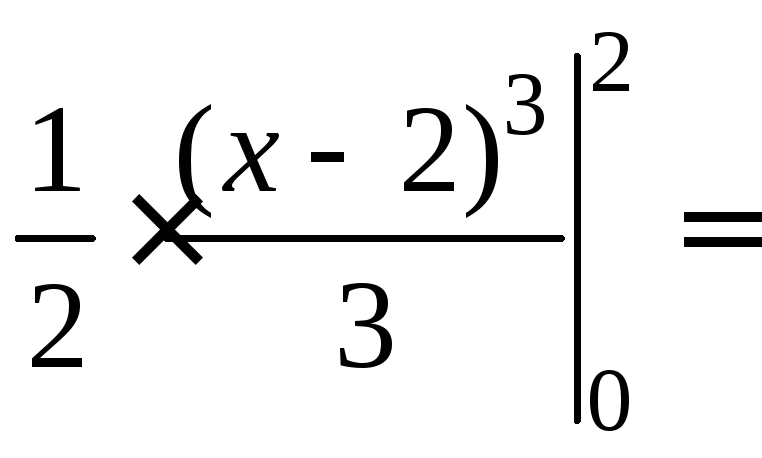
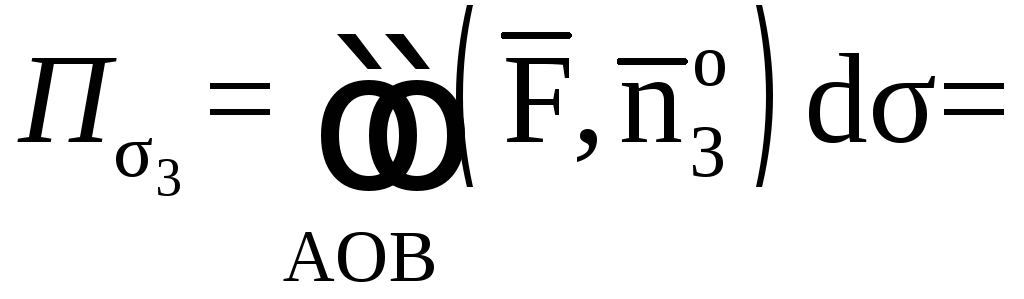
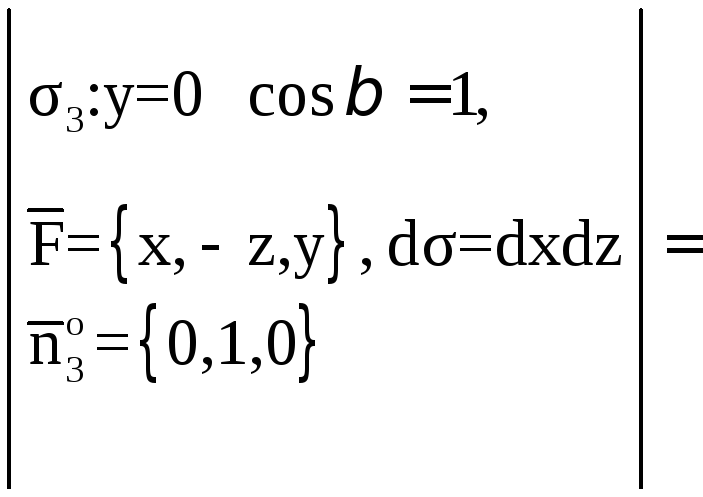
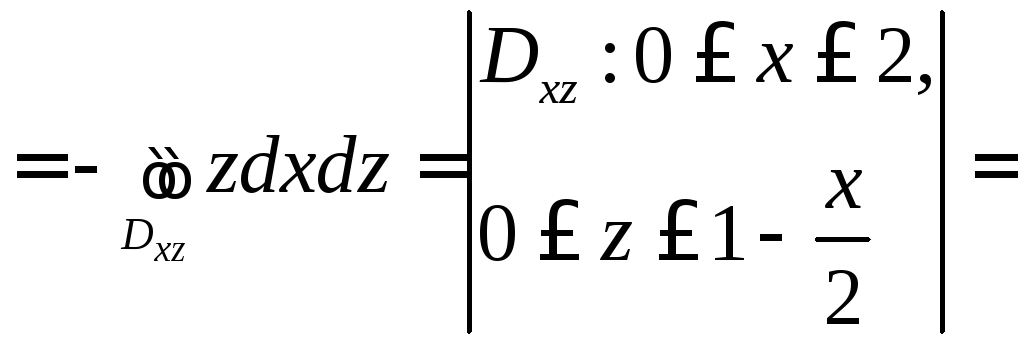
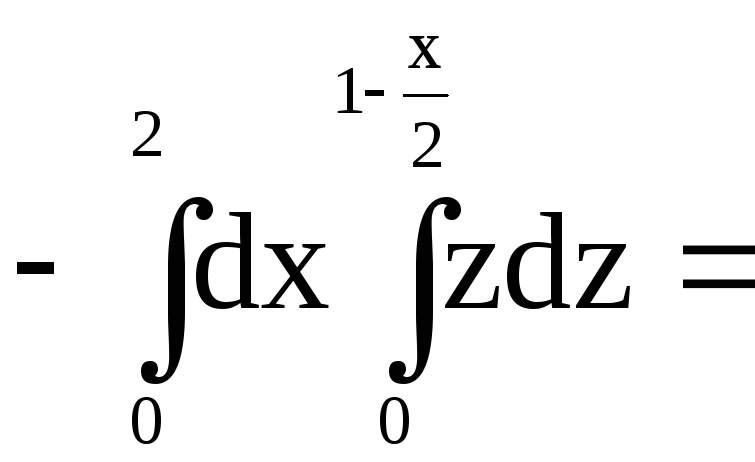
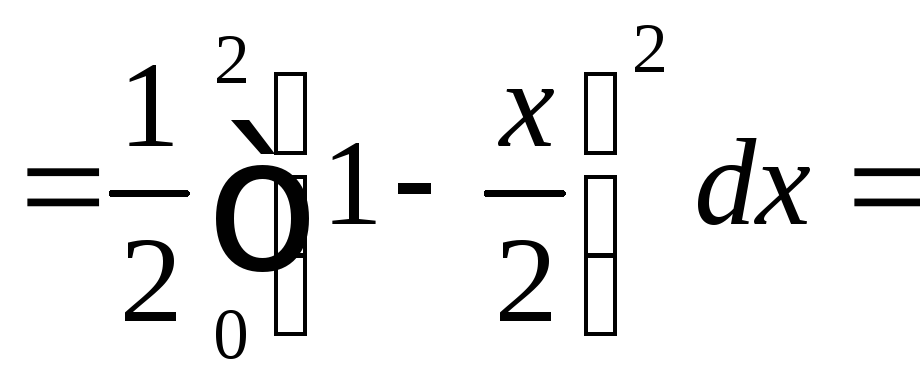
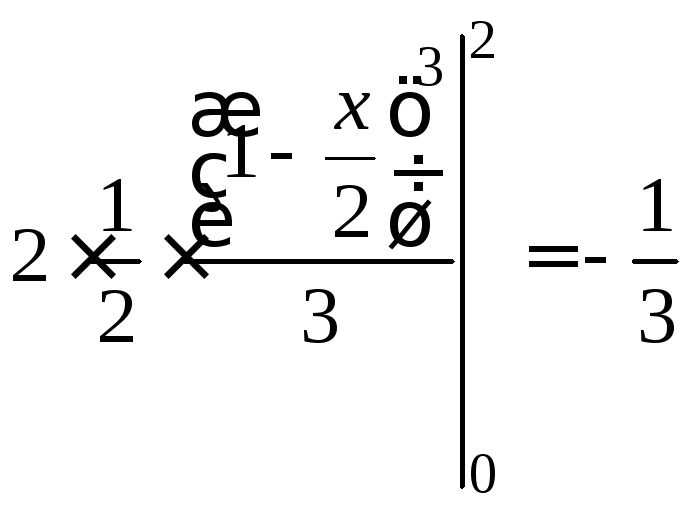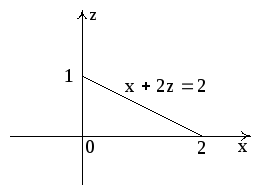
Рис. 9

.

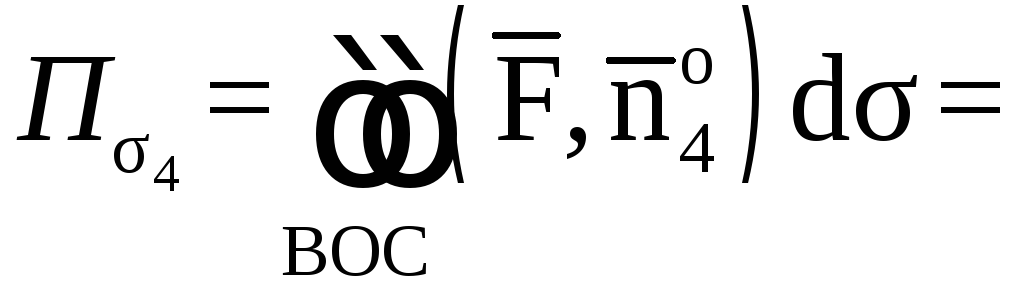
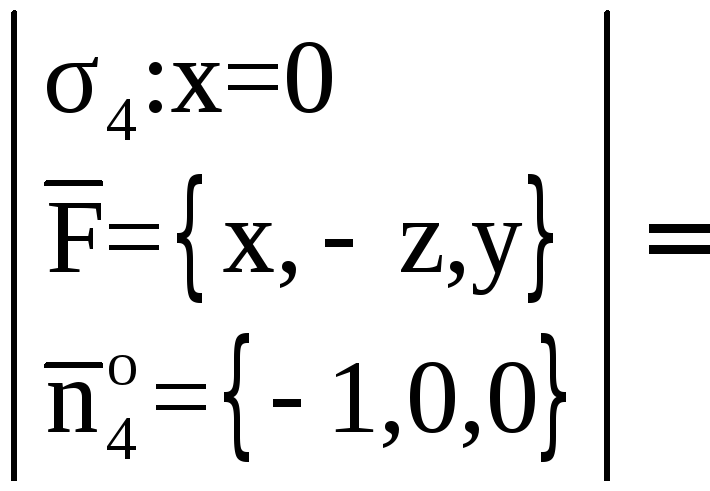
Итак, .

Вычислим поток векторного поля через полную поверхность пирамидыV, применив теорему Остроградского:

.

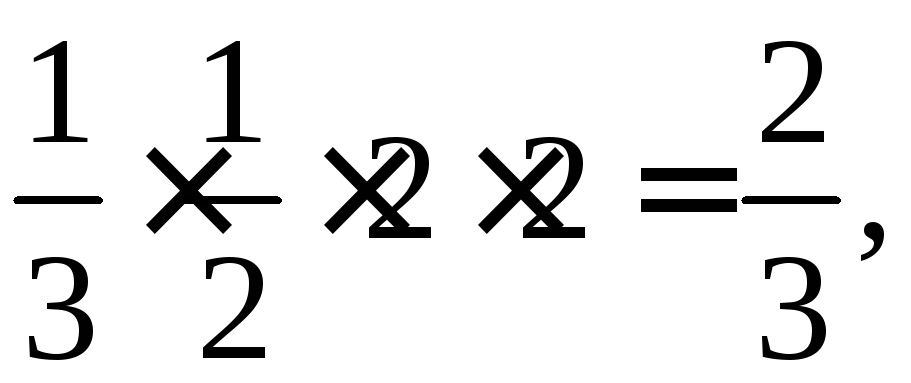
где V − объём пирамиды.

3. Вычислим циркуляцию векторного поля

по контуру треугольника ABCA, где A(2,0,0), B(0,0,1),

C (0,–2,0), непосредственно (рис.10).

.

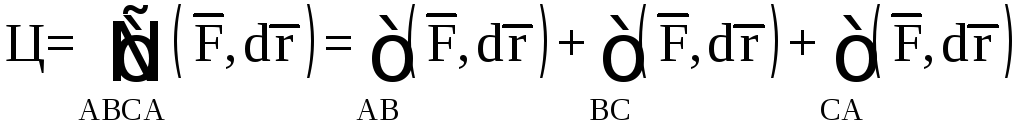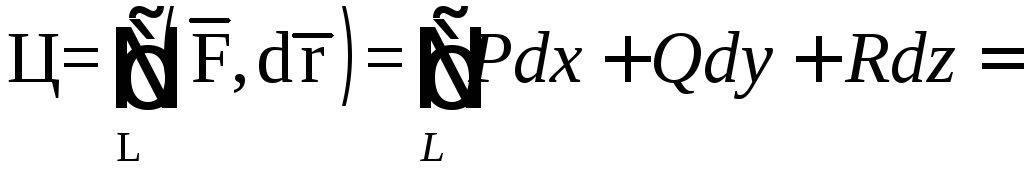
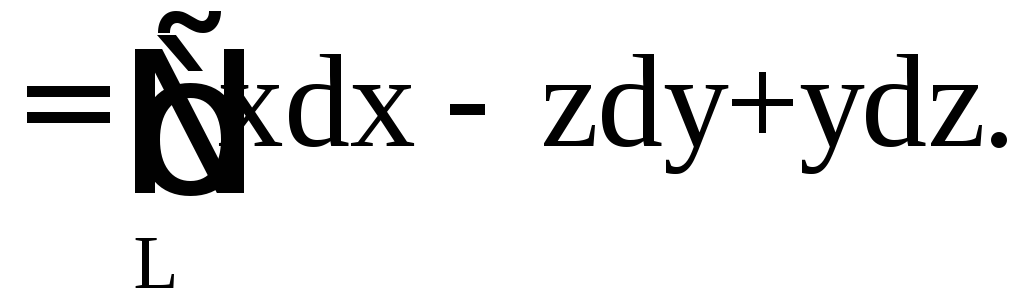
На AB:

на ВС: ;

на СА: .

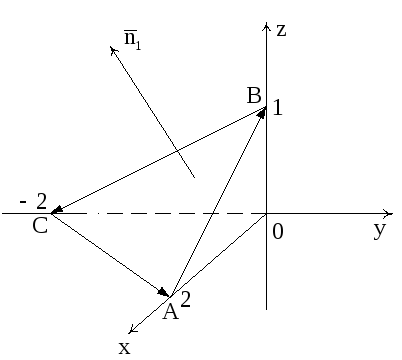
Рис. 10

Тогда .

Вычислим каждый интеграл в отдельности.

.

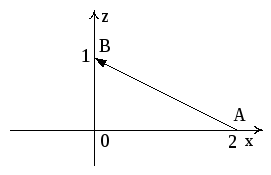
Рис. 11, а

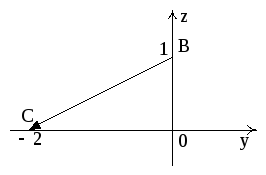
Рис. 11,б

.

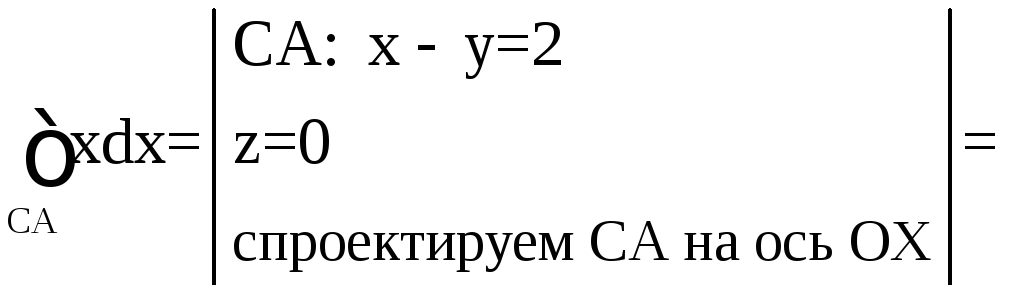
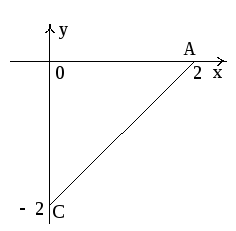
Рис. 11, в

Циркуляция по контуру ABCA

.

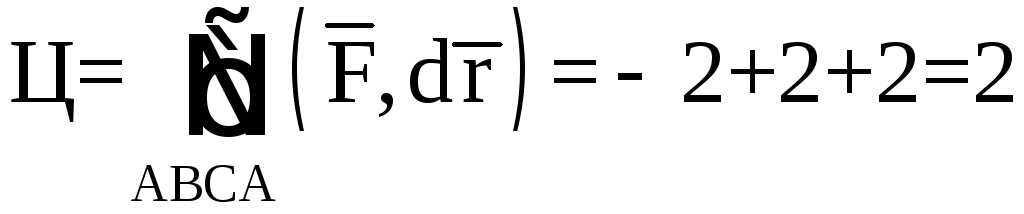Найдем циркуляцию векторного поля по контуру треугольника АВСА, используя формулу Стокса

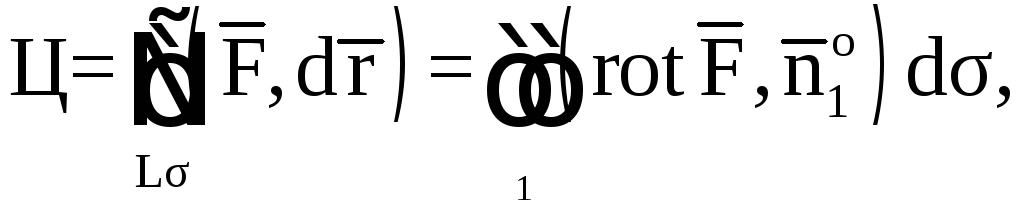
где направление обхода контура L должно быть положительным, то есть согласованным с ориентацией поверхности . В качествеберем верхнюю сторону треугольника АВС, который расположен на плоскости.

В этом случае нормальный вектор к поверхностинаправлен вне пирамидыV и из конца нормали обход контураL (АВСА) в выбранном направлении виден совершающимся против часовой стрелки.

Находим

.

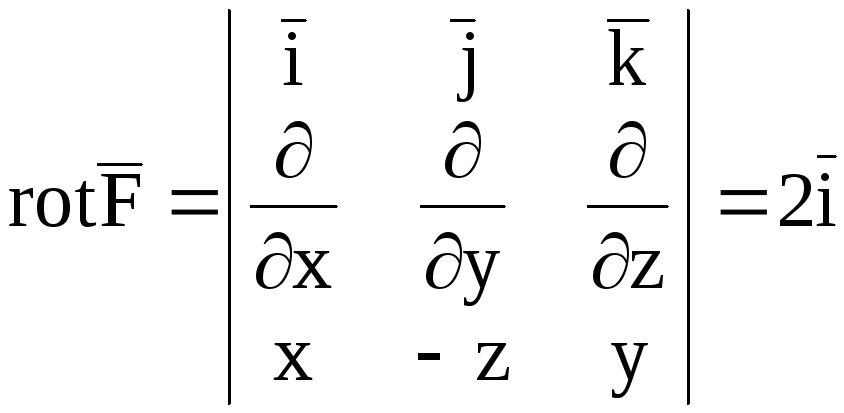Тогда

,

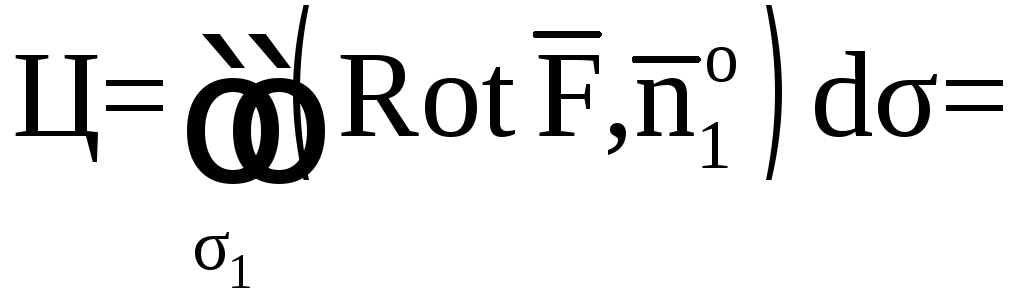
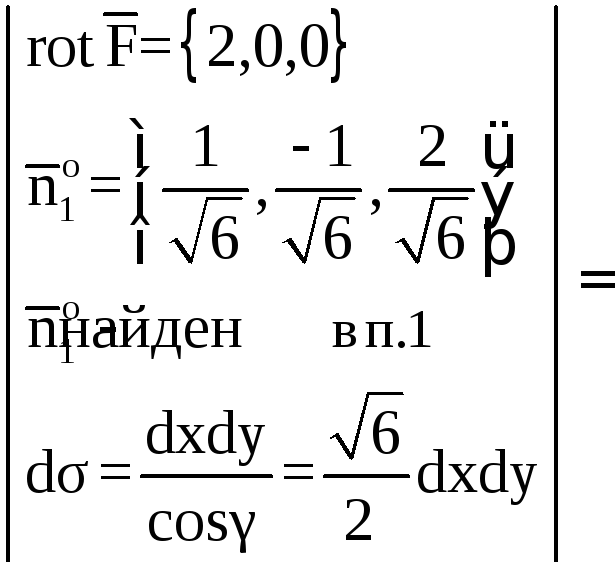
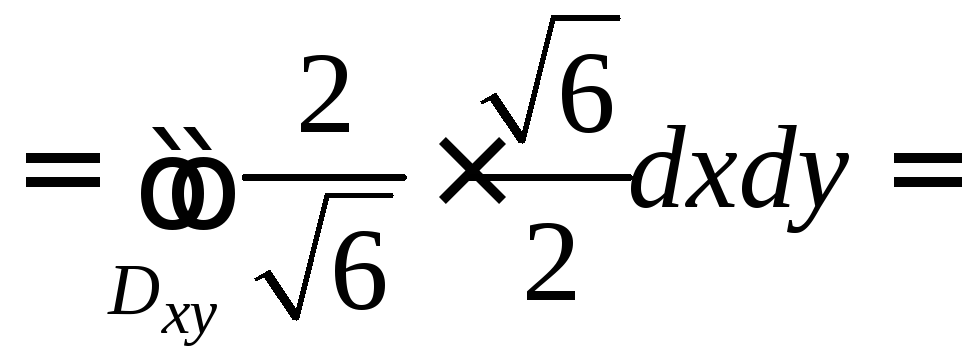
где − площадь

Пример 4. Даны: векторное поле и замкнутая поверхность, составленная частью цилиндрической поверхностии плоскостями,,,,

Поверхность ограничена контуромL; нормаль к поверхности, направленная вне цилиндра.

Вычислить:

1) поток векторного поля через поверхностьв направлении;

2) поток векторного поля через замкнутую поверхностьв направлении внешней нормали к ее поверхности непосредственно и применив теорему Остроградского;

3) циркуляцию векторного поля по замкнутому контуруL непосредственно, и применив теорему Стокса к контуру L и ограниченной им поверхности с нормалью.

Сделать чертеж.

Решение. Найдем поток векторного поля через поверхностьДля этого спроектируем эту поверхность на плоскостьXOZ (проектировать поверхность на плоскостьX0Y нельзя, так как в этом случае ее проекцией является линия) (рис. 12).

.

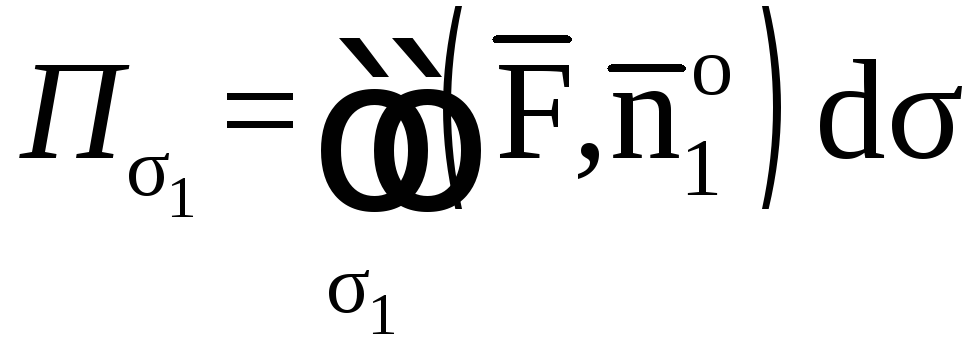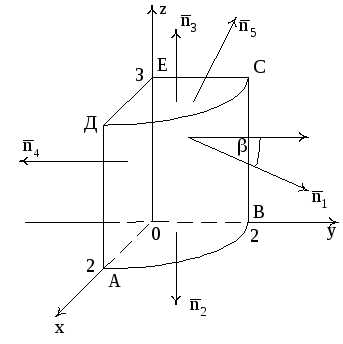
Рис. 12

Из рис. 12 видно, что внешняя нормаль образует острый угол β с положительным направлением оси ОУ, то есть для заданной стороны поверхностиЗапишем уравнение поверхностив виде

и найдем единичный вектор нормали к ней (6).

.

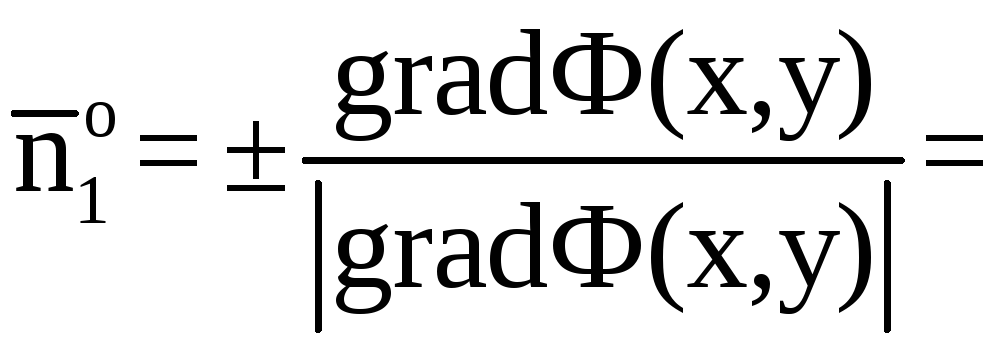
Для того, чтобы полученная нормаль была внешней нормалью к цилиндрической поверхности, угол междуи осью ОУ должен быть острым.

В нашем случае поэтому в полученной формуле для нахожденияиз двух знаков (+) и (–) надо взять знак минус.

Тогда 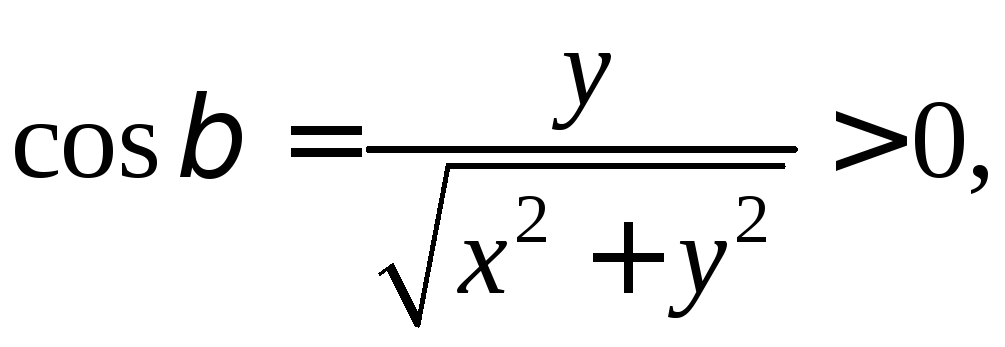что соответствует выбранной внешней стороне цилиндрической поверхности.

Окончательно имеем .

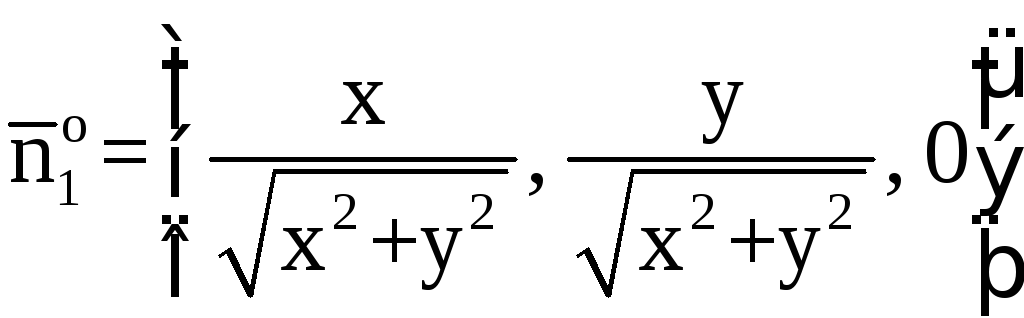Элемент площади .

Таким образом,

.

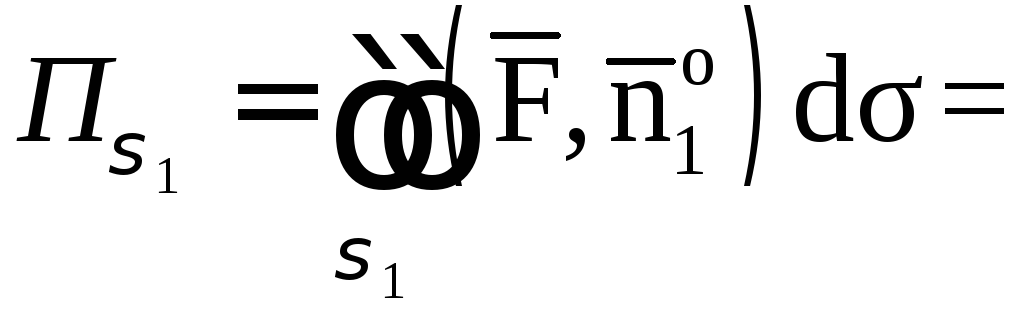
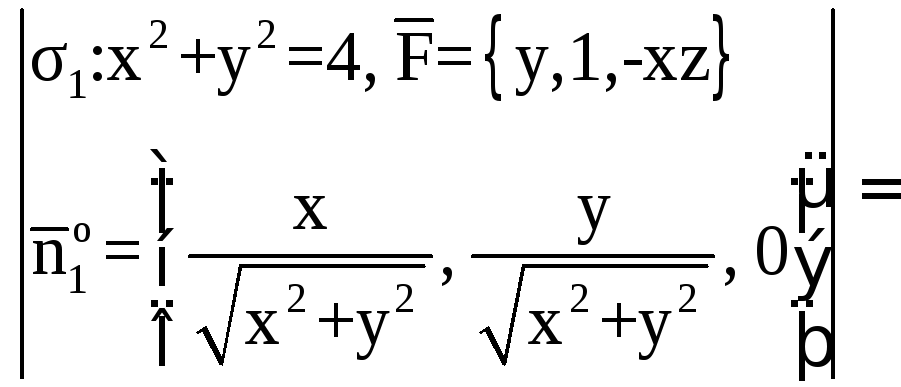
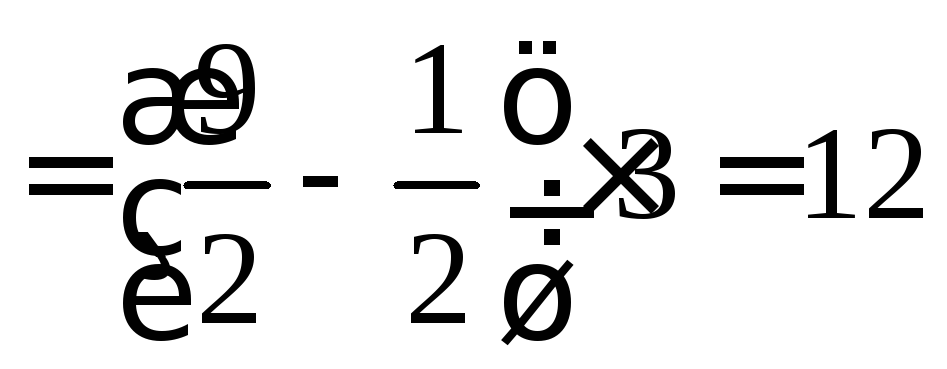Рис. 12, а

Итак, .

2) Найдем поток векторного поля через замкнутую поверхностьв направлении внешней нормали к ее поверхности непосредственно.

,

где ,,,,

.

Итак,

, ;

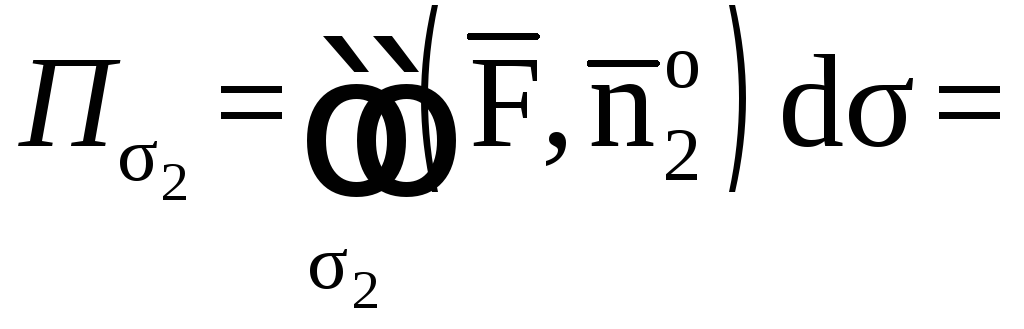
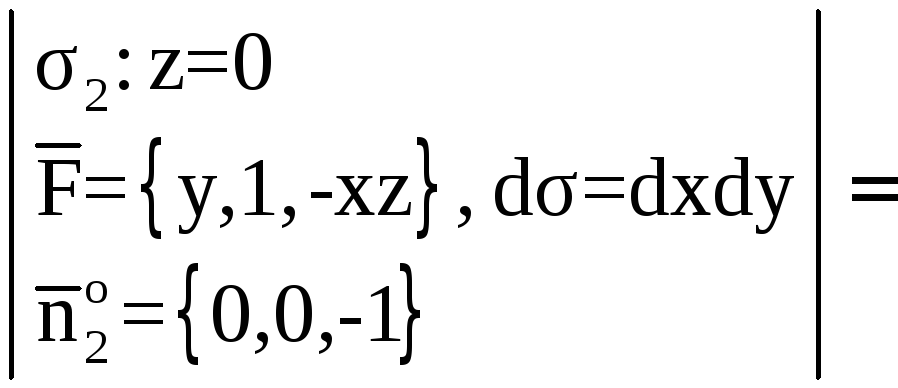
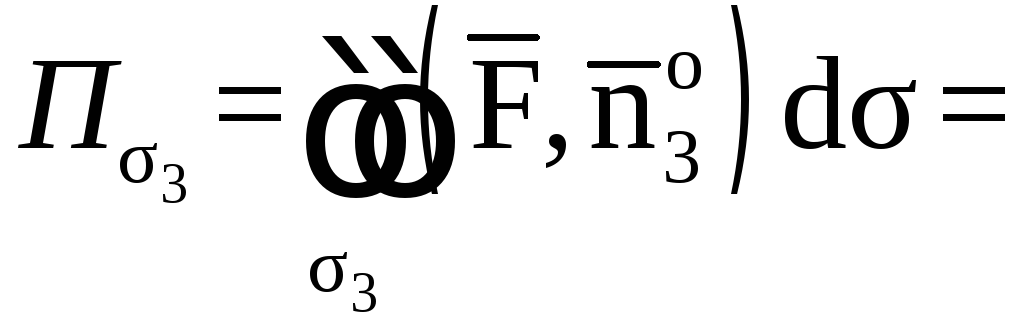
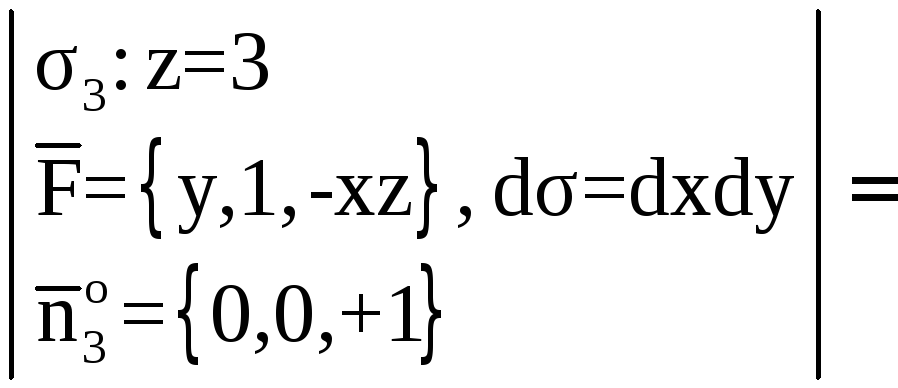
Для вычисления полученного интеграла перейдём в полярную систему координат: якобиан переходаТогда

=

, ;

Рис. 12, б

, ;

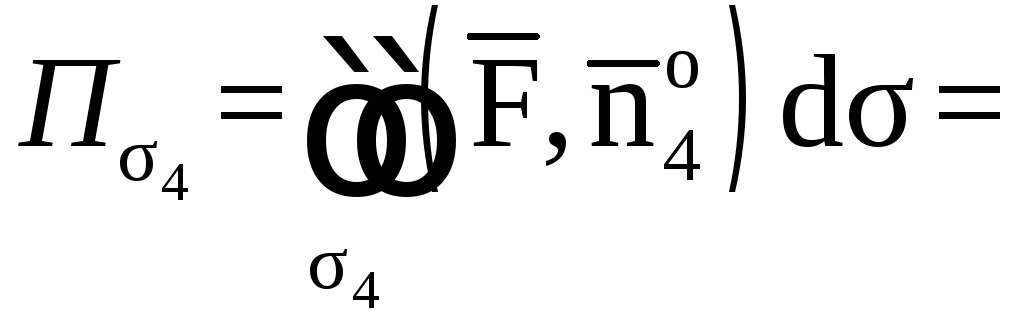
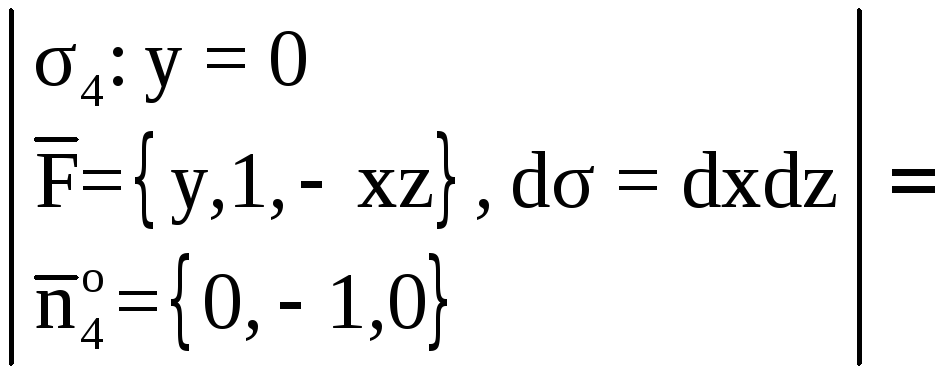
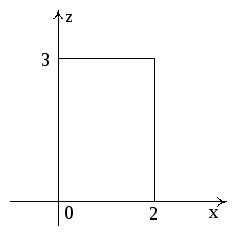
Рис. 12, в

, ;

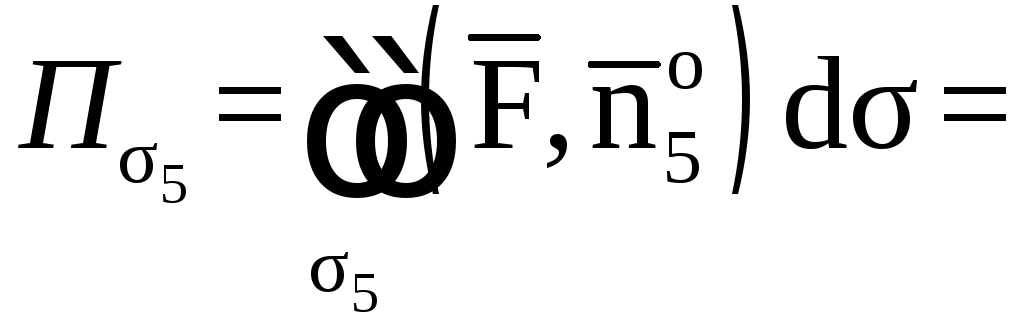
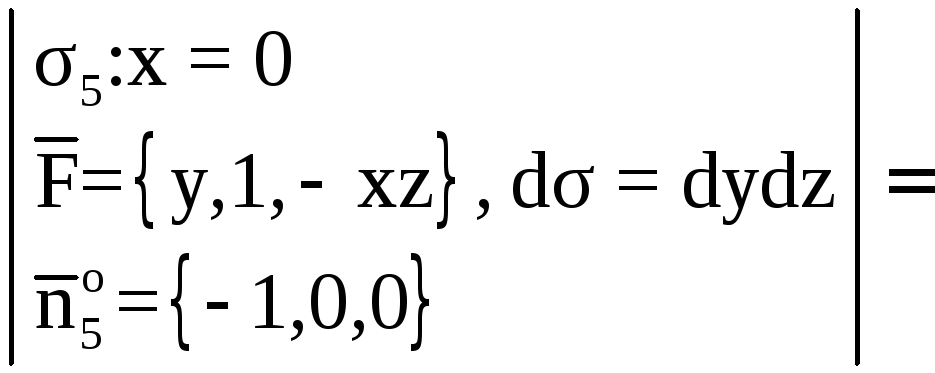
Рис. 12, г

Суммарный поток через замкнутую поверхность равен

.

Найдем поток векторного поля через замкнутую поверхностьв направлении внешней нормали к этой поверхности, применив теорему Остроградского.

.

.

.

.

Тело V проектируется на координатную плоскость X0Y в четверть круга. Поэтому целесообразно этот интеграл вычислять в

цилиндрических координатах.

Рис. 12, д

.

3) Найдем циркуляцию векторного поля по замкнутому контуруL (ABCDA) непосредственно. Контур L состоит из четырех гладких линий AB, BC, CD, DA. Направление обхода контура ABCDA примем положительным, то есть таким, что с конца вектора нормали к внешней стороне поверхностинаправление обхода по контуру было видно совершающимся против часовой стрелки (рис. 13)

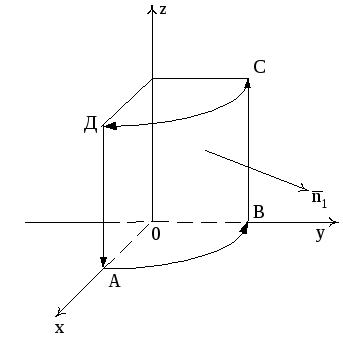
Рис. 13

.

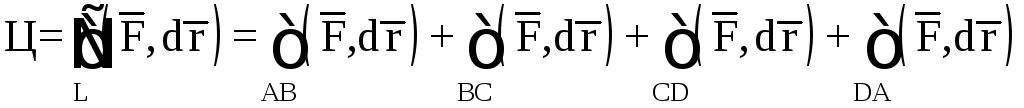Так как , то.

На АВ: ;

на ВС: , , ;

на СД: ;

на DA: , , ,.

Тогда

.

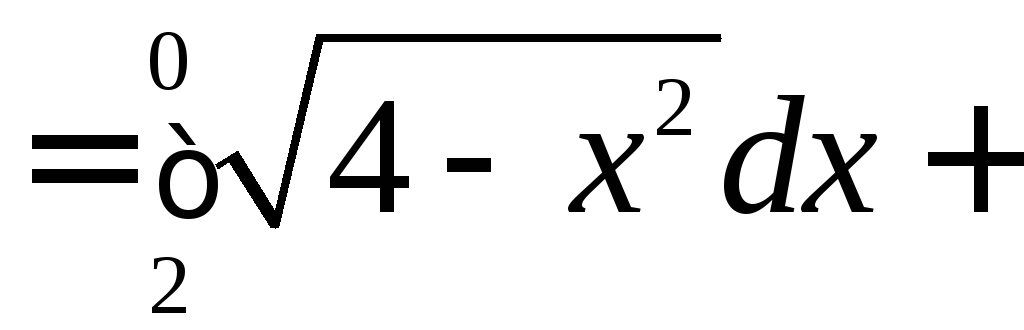
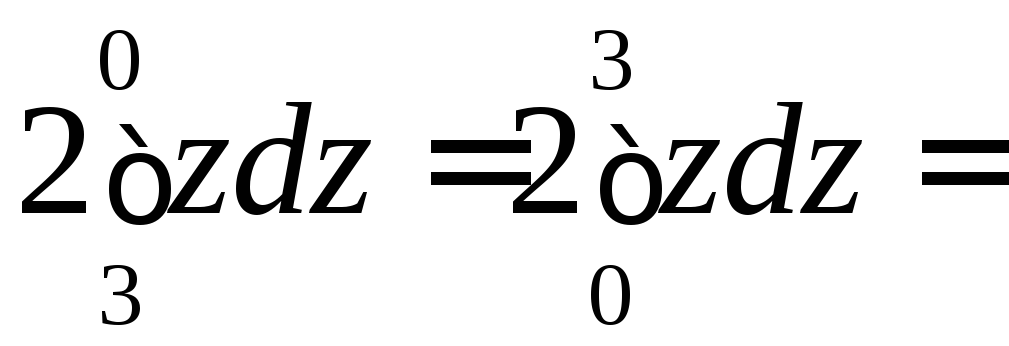
Найдем циркуляцию векторного поля по замкнутому контуру ABCDA, применив теорему Стокса к этому контуру и ограниченной им поверхности с нормалью .

По теореме Стокса, 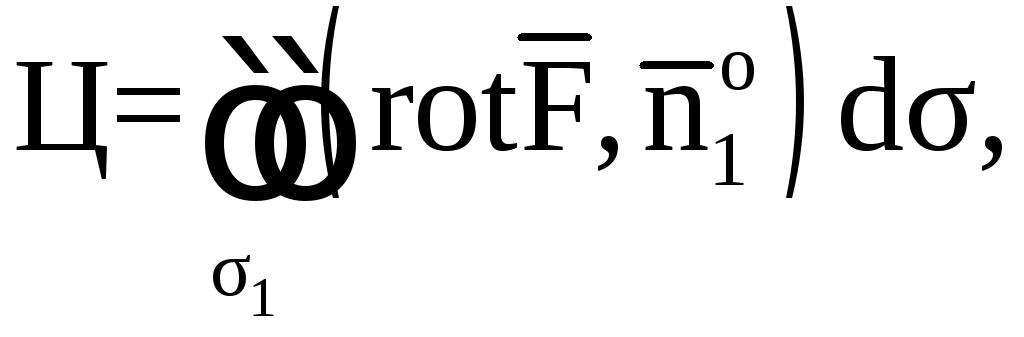где направление обхода контура ABCDA (L) должно быть положительным. В качестве берем внешнюю сторону части цилиндрической поверхности, ограниченной контуром.

Находим

, .

.

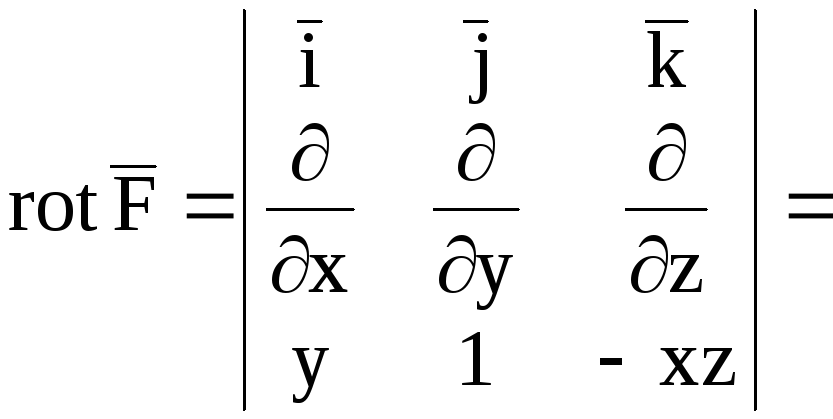
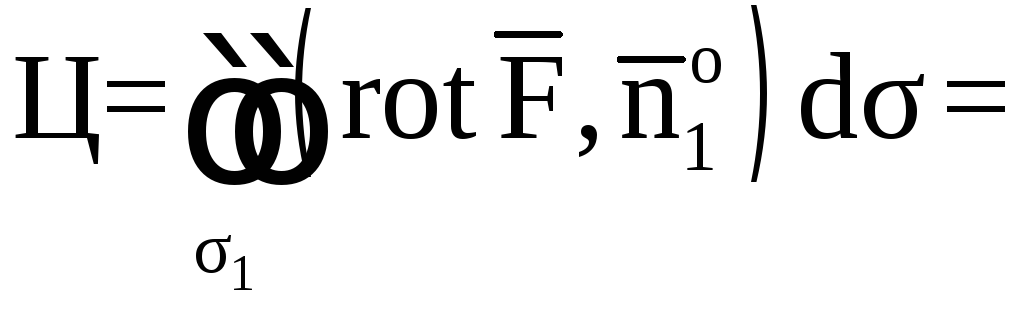
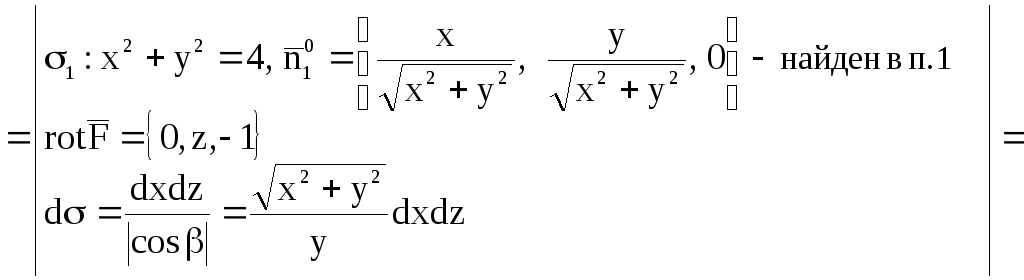
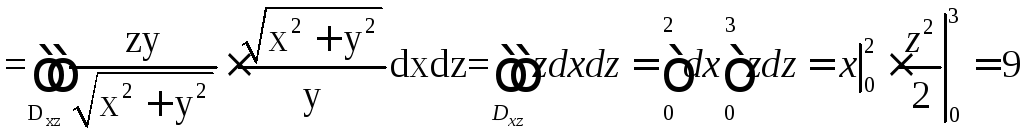Пример 5. Даны векторное поле , поверхность параболоида , отсеченная плоскостью (рис. 14). Найти:

1) поток вектора через внешнюю сторону части поверхности методом замыкания, применив теорему Остроградского;

2) Циркуляцию вектора вдоль контура L в положительном направлении, полученного при пересечении поверхности с плоскостью P, применив теорему Стокса и непосредственно.

Решение. 1) Здесь поверхность незамкнутая, так что к ней нельзя применить теорему Остроградского. Однако вычисление потока по формуле 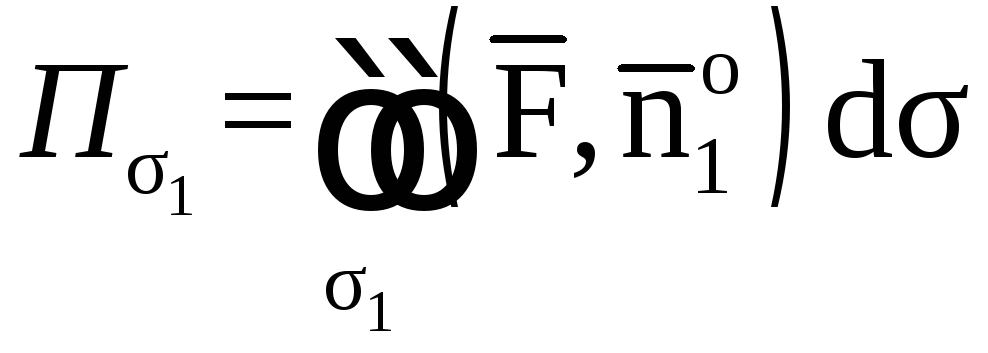приводит к громоздким вычислениям. Поэтому дополним заданную поверхность поверхностью . Тогда получим замкнутую поверхность , состоящую из поверхностей и Очевидно, что , то есть

,

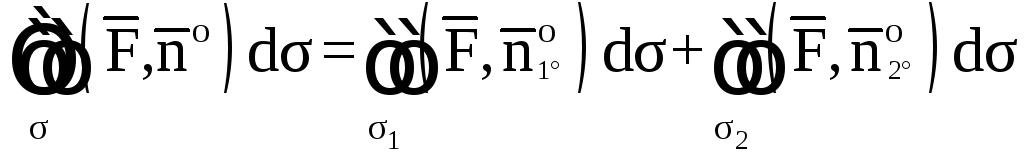откуда искомый поток .

Вычислим и отдельно: .

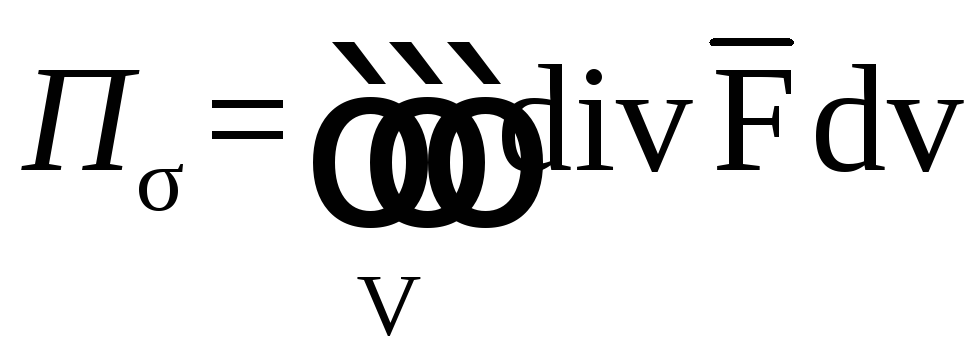Так как , то есть то

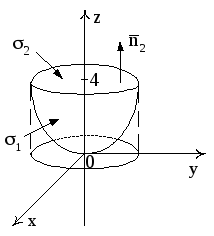
Рис. 14

Тело V проектируется на плоскость X0Y в круг. Вычислим этот интеграл в цилиндрических координатах, в которых уравнение параболоида имеет вид .

,

;

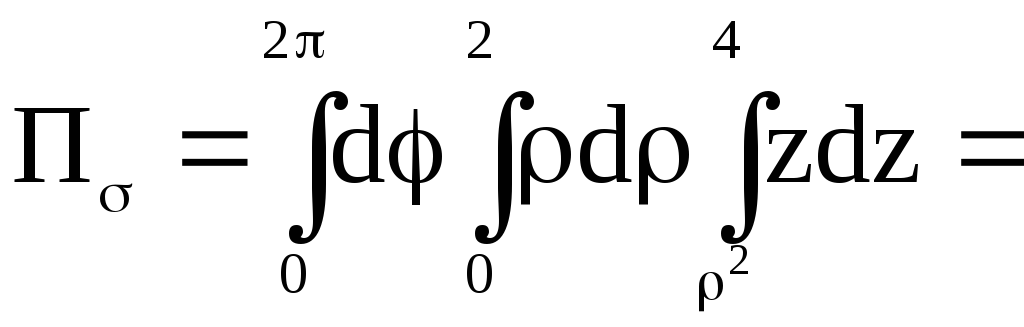
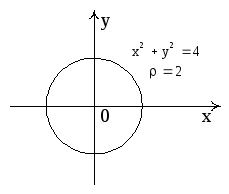
Рис. 15

.

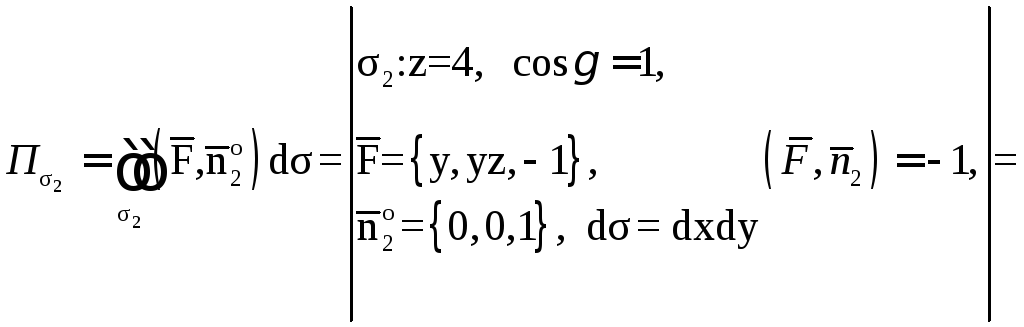
Итак, .

2) Найдем циркуляцию вектора вдоль контура L, полученного при пересечении поверхности с плоскостью по теореме Стокса.

.

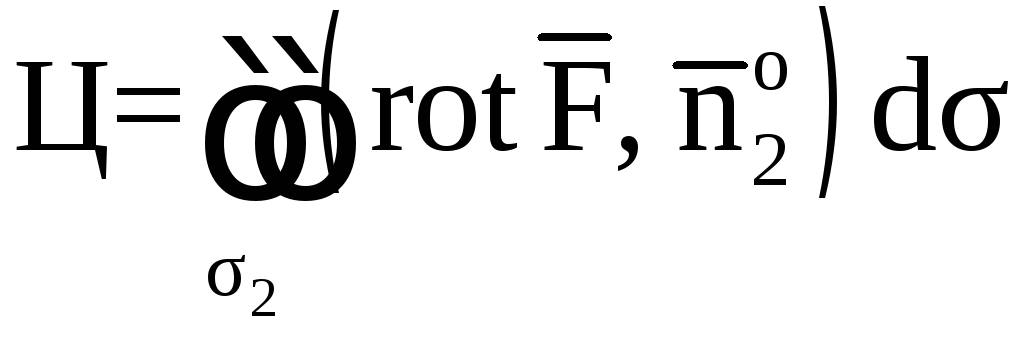Найдем .

.

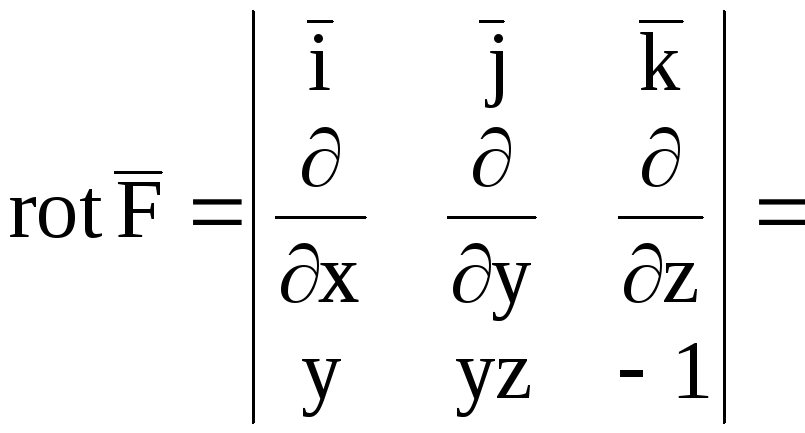
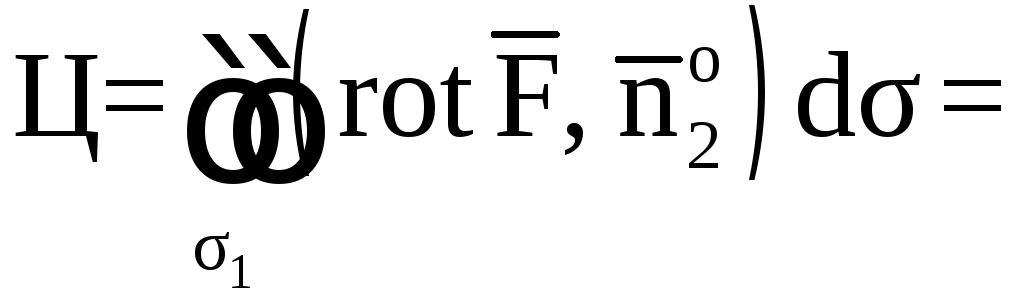
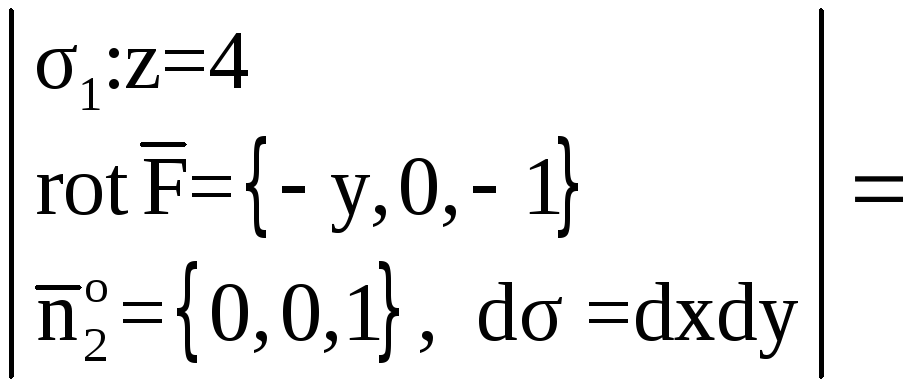
Найдем циркуляцию вектора вдоль окружности в положительном направлении непосредственно.

Параметрическое уравнение контура L имеет вид , , , .

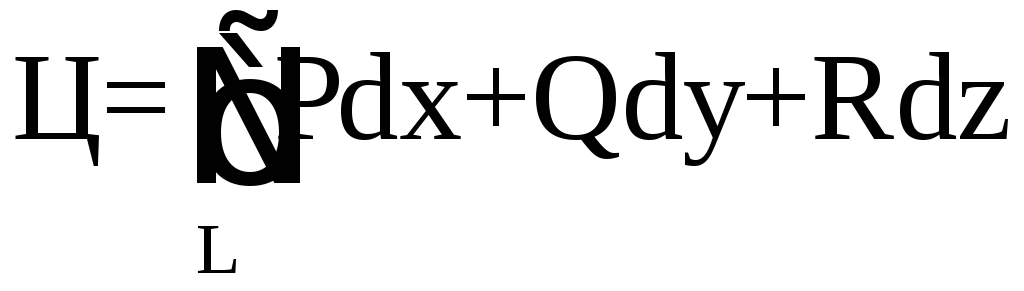Так как , а , то
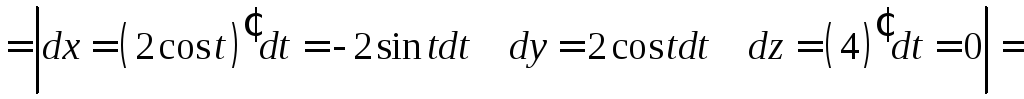