5. Потенциальное поле Векторное поле

называется потенциальным, если вектор является градиентом некоторой скалярной функции , имеющей непрерывные частные производные

. (1)

Функцию u в этом случае называют потенциалом векторного поля .

Напомним, что работой A поля вдоль пути L называется криволинейный интеграл

.

Здесь , −скалярное произведение векторов и .

Работа векторного поля не зависит от пути интегрирования, если для любых точек M₁ и M₂ и любых двух путей L₁ и L₂, соединяющих эти точки

.

Область G трехмерного пространства называется односвязной, если на любой замкнутый контур, лежащий в этой области, можно натянуть поверхность, целиком лежащую в области G.

Например, все трехмерное пространство, внутренность сферы являются односвязными областями.

Необходимым и достаточным условием потенциальности дважды дифференцируемого векторного поля в односвязной области является равенство нулю ротора этого поля:

. (2)

Векторное поле, удовлетворяющее (2), называется безвихревым.

Отметим основные свойства потенциального векторного поля:

1) Криволинейный интеграл II рода от потенциального поля , взятый между двумя точками А и В, не зависит от пути интегрирования и равен разности значений потенциала поля в конце и начале пути интегрирования:

, (3)

поскольку

;

2) Циркуляция потенциального векторного поля по замкнутому контуру (L), целиком лежащему в области непрерывности поля, равна нулю:

;

3) Потенциал может быть вычислен по формуле:

, (4)

где .

Для вычисления интеграла (4) выбирается самый простой путь, например, тот, в котором точки 0 и М соединены ломаной со звеньями, параллельными осям координат. В качестве точки 0 выбирают либо начало координат, либо любую другую точку, лежащую в области непрерывности поля.

Пример. Доказать, что поле

потенциально, найти его потенциал и вычислить работу поля по перемещению материальной точки из точки M₁(1,0,1) в точку .

Решение. Поскольку

,

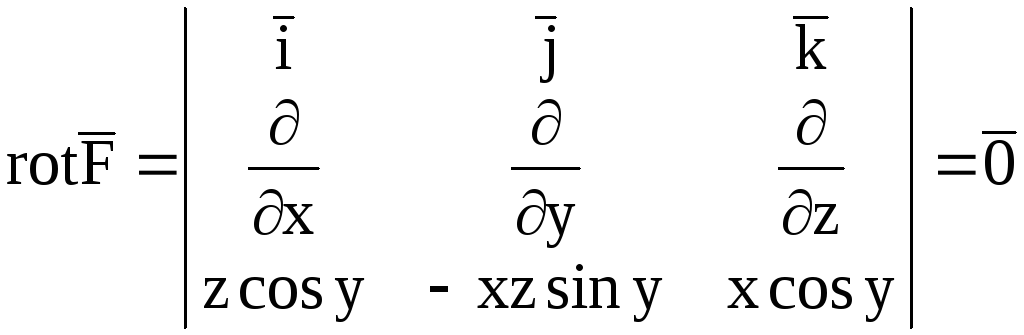то, согласно условию (2), поле является потенциальным.

Найдем его потенциал по формуле (4). За путь интегрирования выбираем ломаную ОАВМ, где О(0,0,0), А(X,0,0), В(X,Y,0), M(X,Y,Z) (рис. 15).

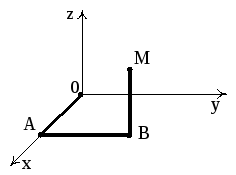
Рис. 15

Тогда получим

,

.

Так как на отрезке ОА: , , то

.

На отрезке АВ имеем: , , , и поэтому .

Наконец, на отрезке ВМ: , , , и, следовательно, .

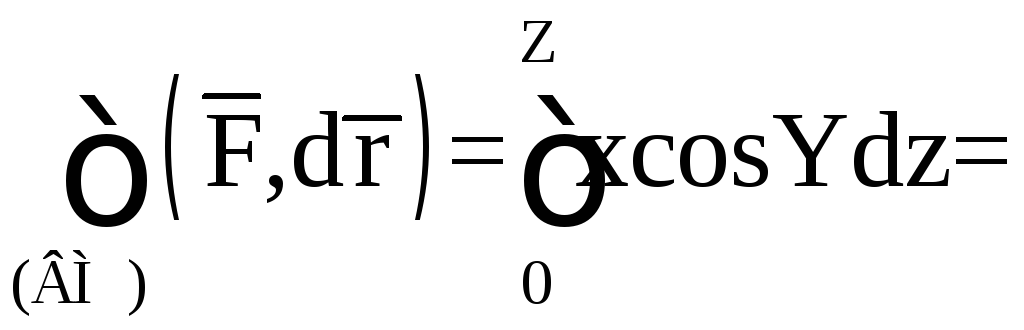
Таким образом, или

.

Сделаем проверку, согласно определению потенциала должно выполняться равенство (1). Имеем

.

Найдем работу A по перемещению материальной точки в поле из т. M₁(1,0,1) в т. М₂(1,,2). Согласно формуле (3)

.

6. Оператор Гамильтона

6.1. Понятие оператора Гамильтона

Рассмотрим символический оператор «набла», называемый оператором Гамильтона:

.

Многие операции векторного анализа можно выразить с помощью оператора Гамильтона, которому присущи как дифференциальные, так и векторные свойства, и это позволяет упростить громоздкие выкладки. Например, если в области пространства задана скалярная дифференцируемая функция , то, умножая «вектор» на скаляр u, получим

.

Если в пространстве задана вектор-функция , где P, Q, R – дифференцируемые функции, то умножая скалярно на , получим

.

Для векторного произведения имеем

.
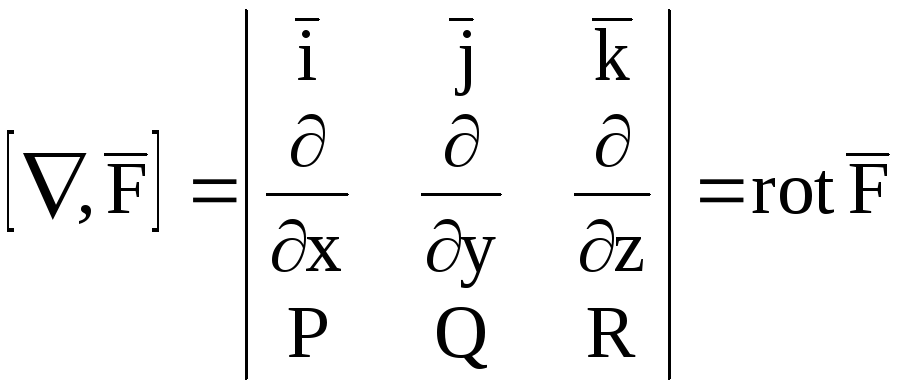