6.2. Дифференциальные операции 1-го порядка Пользуясь свойствами векторных операций, получим
,
То
есть
;
,
или
;
,
то
есть
Оператор Гамильтона обладает как дифференциальными, так и векторными свойствами. При работе с ним следует придерживаться следующих правил:
1)
оператор
действует на все величины, написанные
за ним, и не действует на величины слева
от него;
2)
если оператор
действует на произведение величин, то
в первую очередь учитываются его
свойства, имеющие характер дифференцирования,
а затем уже векторные свойства;
3)
если нужно отметить, что
не действует на какую-либо величину,
входящую в состав сложной формулы, эту
величину помечают индексом с, который
в окончательном варианте убирается.
4) после
того, как учтены дифференциальные
свойства оператора
,
каждое из слагаемых необходимо
преобразовать по правилам векторной
алгебры так, чтобы те величины, на которых
оператор
не воздействует (и только они) вышли из
под знака оператора
.
Это означает, что из двух и более
эквивалентных форм записи, допустимых
по правилам векторной алгебры, надо
выбрать ту форму, в которой под знаком
оператора
остается только сомножитель, на который
он действует, а сомножитель с индексом
«с» выносится из− под знака оператора
.
Пример
1. Найти
.
Имеем
.
Мы учли дифференциальный характер
оператора Гамильтона. Преобразуем
теперь каждое слагаемое по правилам
векторной алгебры. В первом слагаемом
u
– скаляр, на который не действует
оператор
.
Поэтому его можно вынести за знак
оператора Гамильтона и за скалярное
произведение. Второе слагаемое преобразуем
следующим образом:
.
Здесь воспользовались тем, что
.
Окончательно получим
.
Пример
2. Найти
.
Решение.
Пользуясь
тем, что
,
и правилами
1) – 4), имеем
=
.
Здесь мы пользовались тем, что
.
Таким
образом,
.
Пример
3. Найти
.
Решение. Пользуясь известным из векторной алгебры равенством
,
получим
.
Операция
читается так: градиент вектора
по вектору
.
В декартовой системе координат если
то
.
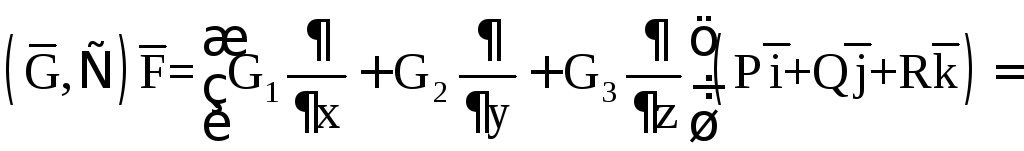
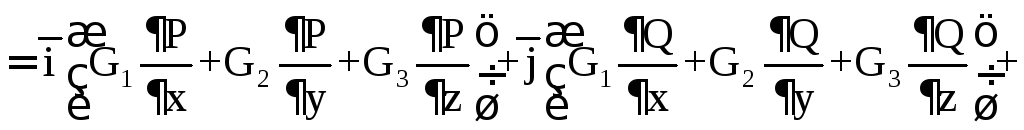
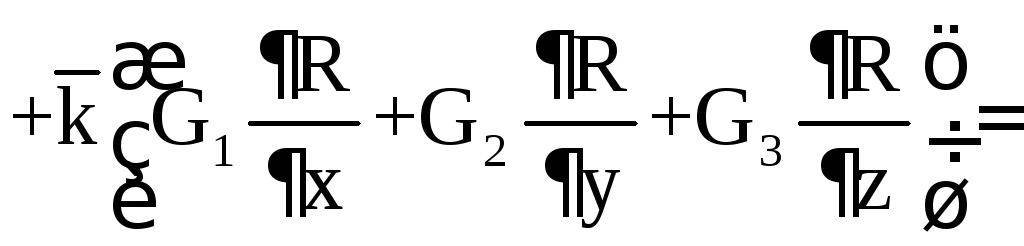
6.3. Дифференциальные операции 2-го порядка
Пусть
скалярное поле u
и координаты векторного поля
дважды непрерывно дифференцируемые
функции.
Рассмотрим
дифференциальные операции 2-го порядка
(в них оператор
действует дважды):
1)
;
(оператор
называют лапласианом).
2)
(всегда = 0);
3)
;
4)
(всегда = 0);
5)
.
Оператор
играет важную роль в математической
физике.
Имеем
,
.
Итак,
.
Оператор
Лапласа
можно представить как скалярное
произведение оператора Гамильтона
на самое себя, то есть
.
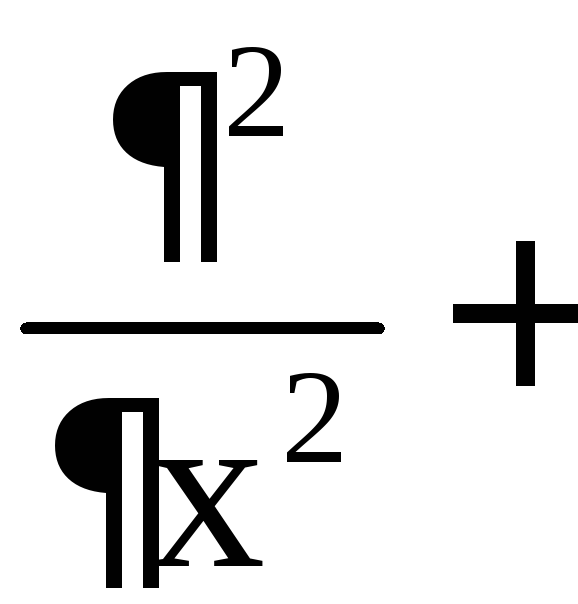
Пример 4.
Показать,
что для скалярной функции
.
Решение. Действуя формально, получим
,
так как векторное произведение двух равных векторов равно 0.
Пример
5. Получить
выражение для
.
Решение. Имеем, пользуясь формулой двойного векторного произведения,
,
где
.
То
есть в декартовой системе координат
,
,
где через
обозначена
проекция вектора
на вектор
.
В общем случае ортогональной криволинейной системы координат (§7).
и вообще говоря
.
Пример
6. Показать,
что
.
Решение.
.
Задачи
1. Используя оператор Гамильтона, доказать следующие равенства:
а)
;
б)
;
в)
;
г)
где
постоянный
вектор,
;
д)
;
е)
;
ж)
где
постоянные векторы,
,
.
2.
Показать, что
.
3.
Доказать, что вектор
ортогонален к
.
4.
Пусть скалярная функция u
удовлетворяет уравнению Лапласа
.
Показать, что вектор
соленоидальный и безвихревый, то есть
,
.
5. Доказать, что:
а)
;
б)
,
где
,
.
7. Ортoгональные криволинейные координаты. Коэффициенты Ламэ. Основные дифференциальные операции теории поля в криволинейных координатах
7.1. Длина дуги
Определение. Длиной дуги S линии γ называют предел длины вписанной в нее ломаной линии при условии, что число звеньев ломаной неограниченно возрастает, а максимум длин звеньев стремится к нулю.
Если
уравнение кривой
,
(1)
и
функции x,
y,
z
,
то, как известно,
,
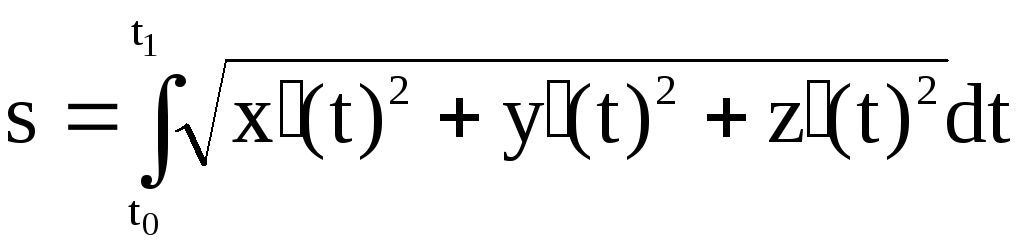. (2)
Дифференцируя (1) по t, имеем
;
.
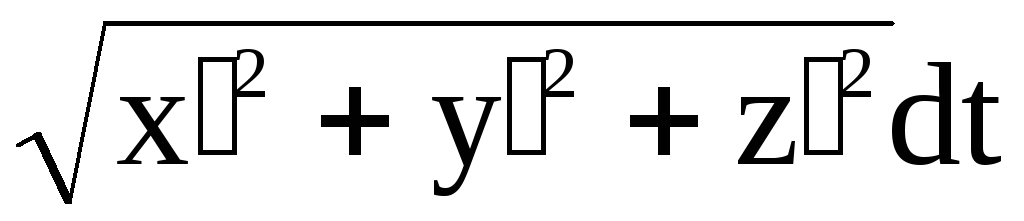. (3)
Сравнивая (2) и (3), получаем
(4)
7.2. Криволинейные координаты. Коэффициенты Ламэ
Наряду с декартовыми координатами в векторном анализе часто применяются криволинейные координаты.
Пример
1. В
цилиндрических координатах положение
точки M(x,y,z)
пространства определяется тремя
координатами
,
где ρ – расстояние от проекции точки M
на плоскость X0Y
точки N
до начала координат, φ – угол
между положительным направлением оси
0X и вектором
.
Третьи координаты точки М в цилиндрической
и декартовой системе координат совпадают.
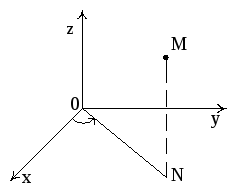
Рис. 16
При этом
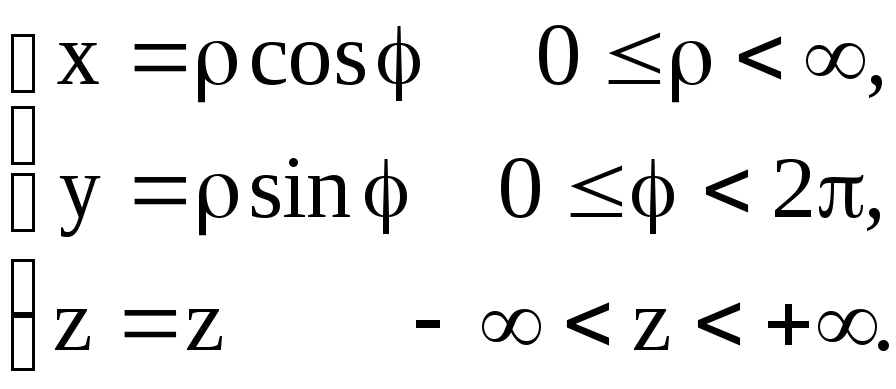
Пример
2. Поставим
в соответствие каждой точке M(x,y,z)
тройку чисел
,
где r
– расстояние от точки M
до начала координат, φ – угол между
положительным направлением оси ОХ и
вектором
(см. рис.17), Θ – угол между положительным
направлением оси 0Z
и вектором
.
Здесь точка N
- проекция точки M
на плоскость X0Y.
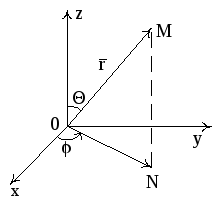
Рис. 17
Упорядоченная
тройка чисел
называется сферическими координатами.
Связь декартовых координат со сферическими
определяется формулами:
Можно
считать, что
,
.
Пусть
каждой точке M
трёхмерного пространства отвечает
упорядоченная тройка чисел
,
и обратно, каждой тройке чисел отвечает
единственная точка M.
В этом случае величины
называют криволинейными координатами
точки M.
Так
как любой точке M
можно поставить в соответствие ее
декартовы (x,
y,
z)
и криволинейные
координаты, то это означает, что между
переменными x,
y,
z
и
существует функциональная зависимость
(5)
Причем
система (5) должна быть однозначно
разрешима в области изменения
.
Определение.
Множество точек M
пространства, у которых фиксирована
одна из координат, называется координатной
поверхностью.
Множество
точек M
,
у которых фиксированы две координаты,
называются координатной линией.
Очевидно, что координатные линии являются пересечением координатных поверхностей.
Пример 3. В
цилиндрической системе координат
координатные поверхности
– круговые
цилиндры.
полуплоскости,
примыкающие к оси 0Z;
плоскости,
параллельные плоскости X0Y.
Пример 4.
В сферической
системе координат координатные
поверхности
сферы
с центром в начале координат,
полуплоскости,
примыкающие к оси 0Z,
круговые полуконусы с осью 0Z.
Векторное уравнение координатных линий получается из равенства
,
в котором фиксированы две переменные.
Зафиксируем
точку
и проведем через нее три координатные
линии:
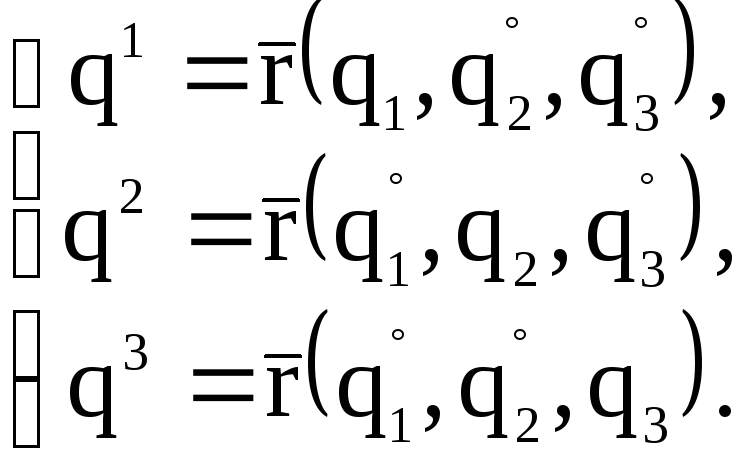
В точке M0 эти линии имеют касательные, векторное уравнение которых имеет вид:
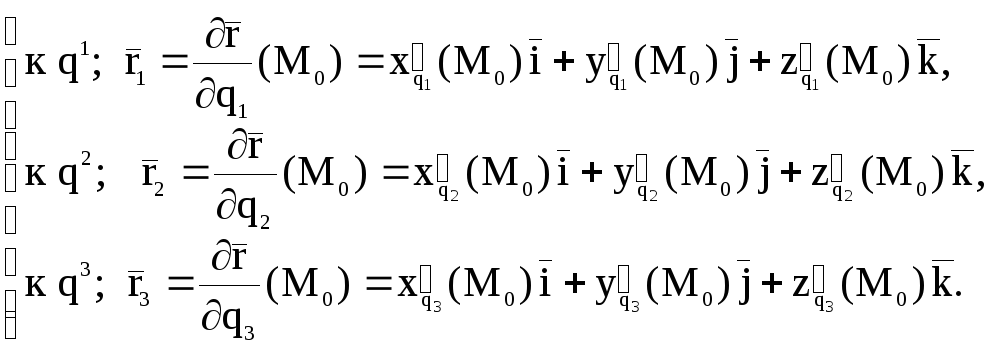(6)
Оказывается,
совокупность векторов
,
которые меняются по величине и направлению
при изменении точкиM0,
линейно независимы в каждой точке, то
есть образуют базис. Его называют
локальным базисом.
Итак,
в каждой точке
мы построили локальный базис (6), элементы
которого меняются по величине и
направлению при переходе от точки к
точке.
Определение. Система координат называется ортогональной криволинейной системой, если в любой точке пространства координатные линии пересекаются под прямым углом.
Так как ортогональность координатных линий означает ортогональность их касательных, то необходимым и достаточным условием для ортогональности криволинейной системы координат является равенство нулю скалярного произведения
,
где
,
.
Задача. Проверить, что цилиндрическая и сферическая системы координат – ортогональные криволинейные системы координат.
Итак,
основное отличие криволинейных координат
от декартовых состоит в том, что в
декартовой системе векторы
постоянны во всех точках пространства
и равны соответственно
.
Во всякой другой системе они будут,
вообще говоря, изменять свои направления
при переходе от точки к точке.
Определение.
Длины базисных
векторов
называются коэффициентами Ламэ и
обозначаются
.
Коэффициенты Ламэ находят по формулам
.
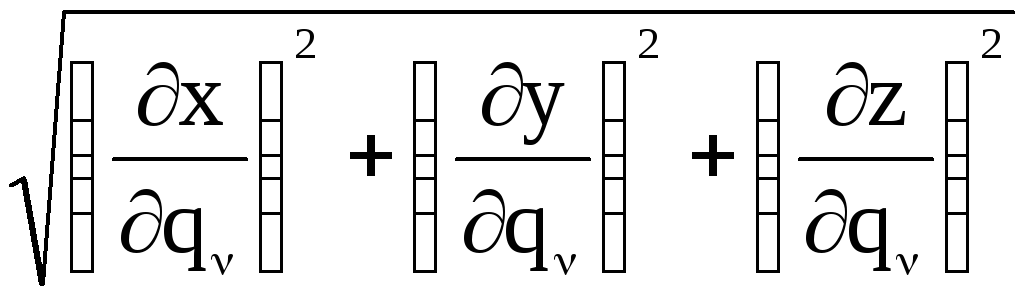
В ортогональной криволинейной системе координат векторы
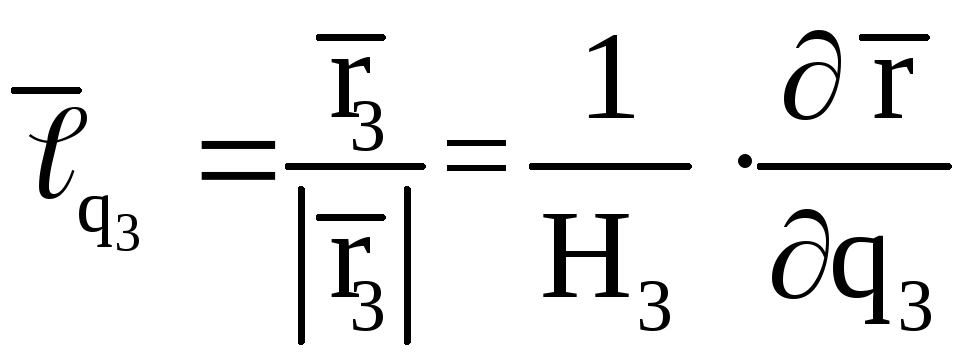
имеют
единичную длину, образуют ортонормированный
локальный базис и для любого вектора
(7)
Так как дифференциал дуги ds совпадает с длиной дифференциала радиус-вектора (4) и вдоль каждой координатной линии меняется только одна переменная, то
;
;
.
В
самом деле
.
Но
вдоль координатной линии q1,
,
.
Следовательно,
,
Тогда
.
Аналогично доказываются и остальные две формулы.
Рассмотрим
бесконечно малый прямоугольный
параллелепипед, ребрами которого служат
«отрезки» координатных линий
.
Для
площадей граней
и объемаdv
этого параллелепипеда можно записать
,
,
(8)
Пример 5. Найти коэффициенты Ламэ в цилиндрической
системе координат
Решение
.
.
.
Пример 6. Найти коэффициенты Ламэ в сферической системе координат
Решение
.
.
.