2. Скалярные и векторные поля. Основные дифференциальные операции в декартовой системе координат

Если каждой точке М некоторой области пространства поставлено в соответствие число (скаляр) , то говорят, что задано скалярное поле. В прямоугольной системе координат, скалярное поле станет функцией трех переменных .

Пример скалярных полей дает поле температур, потенциал электромагнитного поля и т.д.

Пусть − единичный вектор. Он задает некоторое направление.

Определение. Производной от функции по направлению называется предел (если он существует)

где вдоль луча, выходящего из т. M₀ по направлению вектора −длина вектора Пусть функция, непрерывно дифференцируемая в точке M₀,

Тогда

(1)

Определение. Градиентом скалярного поля φ называется вектор

. (2)

Свойства градиента:

а) из формулы (1) следует, что ;

б), так как

где угол между векторами и ;

в) если , то есть направления и совпадают, то

.

Отсюда следует, что направление характеризуется тем, что производная по направлениюбудет наибольшей. То есть– вектор, направленный в сторону наибольшего возрастания функции φ.

г) вектор в каждой точке направлен по нормали к поверхности уровня , проходящей через эту точку в сторону возрастания поля.

Пример 1. Даны скалярное поле точки , . Найти:

1) градиент поля в точке M₀;

2) производную функции в точке M₀ по направлению от точки к точке M₁;

3) производную функции в точке M₀ в направлении градиента функции в этой точке;

4) угол между градиентами данной функции в точках M₀ и M₁.

Решение.  1)  Находим частные производные функции и их значения в точкеM₀:

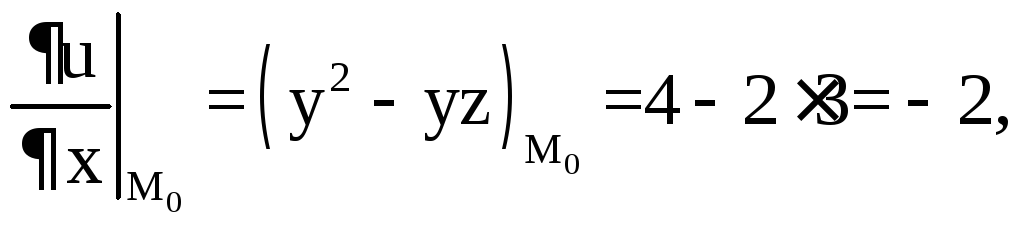
По формуле (2) находим

2) Найдем производную скалярного поля в точке M₀(1,2,3) по направлению, идущему к точке M₁(2,4,5).

Это направление определяется вектором

, поэтому по формуле (1)

,

где , , , получим

, , ,

.

3) Найдем производную функции в точке по направлению .

Так как то направляющие косинусы

, ,

и .

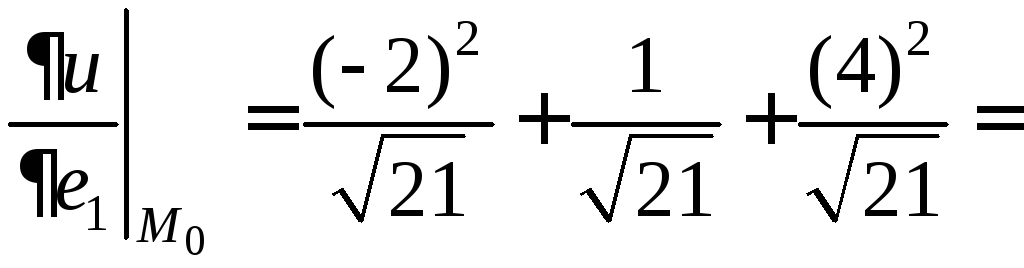
4) Найдем угол между градиентами данной функции в точках и .

Находим частные производные функции и их значения в точке M₁.

,

,

.

Тогда .

Угол φ между градиентами и находим по формуле

то есть

=

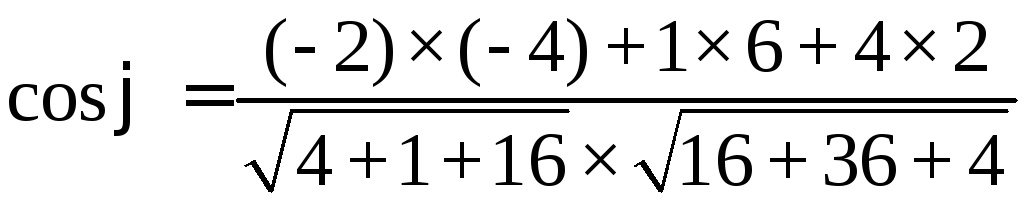Пример 2. Найти производную скалярного поля в точке M₀(1,1), принадлежащей параболе по направлению:

1) этой кривой (в сторону возрастания абсциссы); 2) внешней нормали к этой кривой.

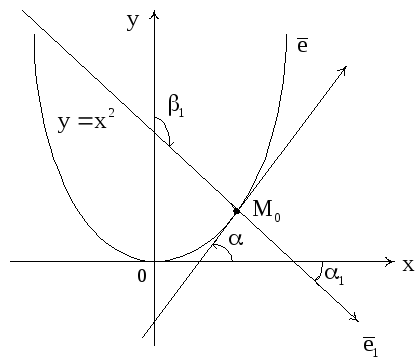
Рис. 2

Решение. Направлением параболы в точке M₀(1,1) считается направление касательной к параболе в этой точке. Пусть α – угол наклона касательной к кривой в точке M₀. Тогда

.

Частные производные функции в точке M₀:

, .

По формуле получим

.

2) Пусть угол наклона внешней нормали к кривой в точке M₀. Тогда ,

.

.

Пример 3. Для скалярной функции найти градиенты в точках P₀(1,6) и P₁(0,0), угол между и , производную по направлению , где вектор перпендикулярен прямой x – 3y = 4 и направлен в сторону убывания поля.

Решение. Вычислим частные производные функции z в точках P₀ и P₁:

; ;

; .

Тогда

Поскольку то угол между и равен нулю. Поскольку то угол междуиравен нулю.

Найдем производную по направлению. Так как вектор перпендикулярен прямойто он коллинеарен вектору нормалиэтой прямой. Кроме того,должен быть направлен в сторону убывания поля. Согласно свойству градиента в этом случае угол между векторомидолжен быть тупым, а

Вычислим Поэтому в качестве векторавозьмем векторВычислим.

Тогда имеем

.

Определение. Если в каждой точке M некоторой области G трехмерного пространства задан вектор, то говорят, что задано векторное поле .

В декартовой системе координат задание поля

(3)

эквивалентно заданию трех скалярных функций P, Q, R.

Примеры: электростатическое поле, магнитостатическое поле и т.д. Для векторного поля (3), где P, Q, R – непрерывные функции своих аргументов, имеющие непрерывные частные производные первого порядка, можно ввести две операции: дивергенцию и ротор.

Определение. Дивергенцией векторного поля называется скалярная функция

. (4)

Ротором (вихрем) векторного поля называется векторное поле

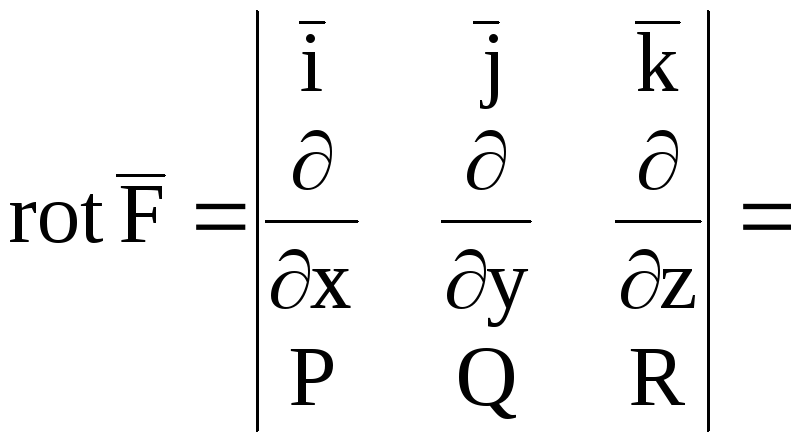
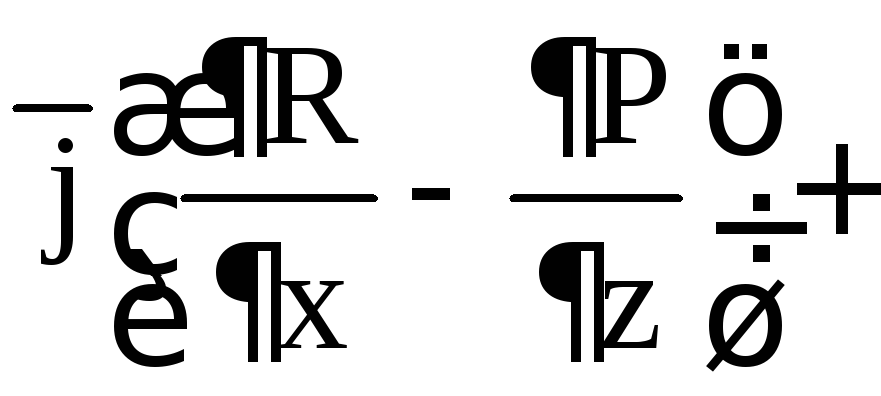
. (5)

Замечание. Данные определения зависят от системы координат. Ниже (§7, п.3) даны определения,, инвариантные относительно системы координат.

Пример 4. Найти дивергенцию векторного поля

.

Решение.

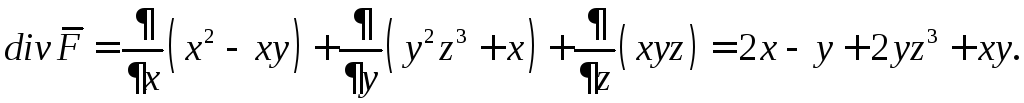Пример 5. Найти ротор векторного поля

.

Решение.

.

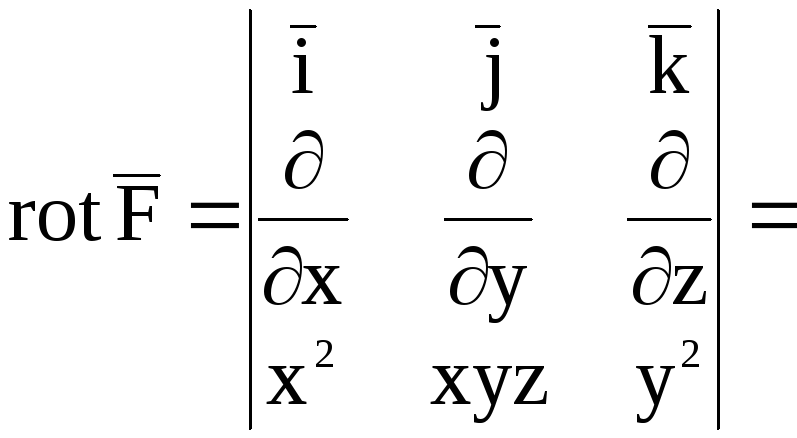
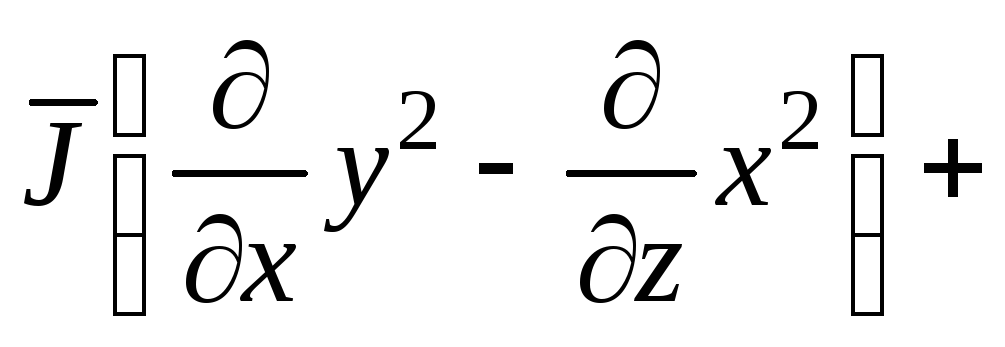
Если во всех точках M области

G , (6)

то говорят, что поле соленоидально в этой области.