
- •VII. Интегральное исчисление функции одного переменного
- •1. Неопределённый интеграл
- •2. Таблица основных неопределённых интегралов
- •3. Основные свойства неопределённого интеграла
- •4. Интегрирование методом замены переменного
- •5. Интегрирование по частям
- •6. Интегрирование рациональных функций Интегрирование рациональной функции
- •7. Интегрирование тригонометрических функций
- •8. Интегрирование некоторых иррациональных функций
- •9. Определённый интеграл
- •10. Несобственные интегралы
- •11. Вычисление площадей плоских фигур
- •12. Вычисление длины дуги
- •13. Вычисление объёмов тел
- •14. Приближённое вычисление определённых интегралов
- •Задание 7.1
- •Задание 7.2
- •Задание 7.3
- •Задание 7.4
- •Задание 7.5
- •Задание 7.6
- •Задание 7.7
- •Задание 7.8
- •Задание 7.13
- •Задание 7.14
- •Задание 7.15
- •Задание 7.16
- •Задание 7.17
- •Задание 7.18
- •Задание 7.19
- •Задание 7.20
- •Задание 7.21
- •Задание 7.22
Задание 7.16
Вычислите несобственные интегралы или установите их расходимость.
1.
 ; 7.
; 7. ;
13.
;
13.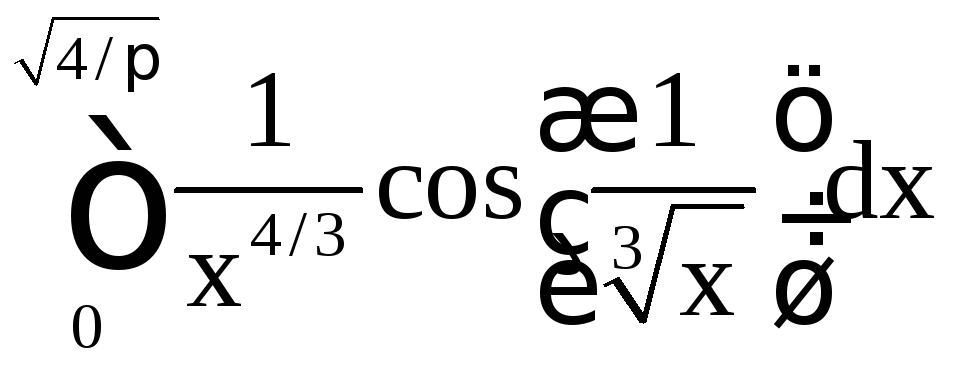 ;
;
2.
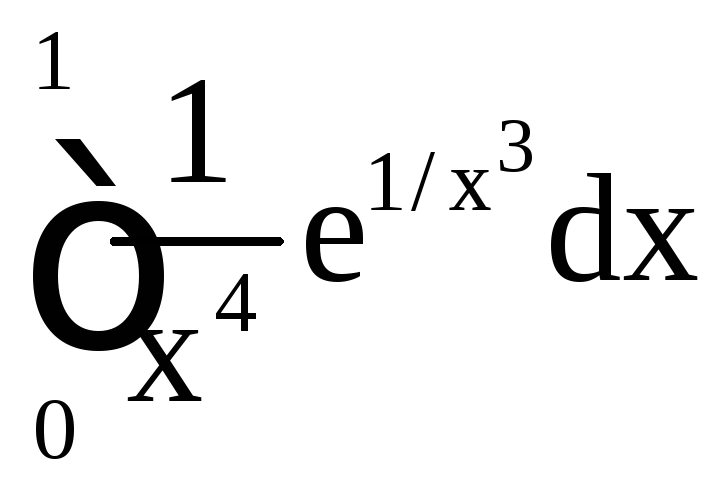 ; 8.
; 8. ; 14.
; 14. ;
;
3.
 ; 9.
; 9. ; 15.
; 15. ;
;
4.
 ; 10.
; 10. ; 16.
; 16. ;
;
5.
 ; 11.
; 11. ;
17.
;
17. ;
;
6.
 ;
12.
;
12. ;
18.
;
18. ;
;
19.
 ; 23.
; 23. ;
27.
;
27. ;
;
20.
 ;
24.
;
24.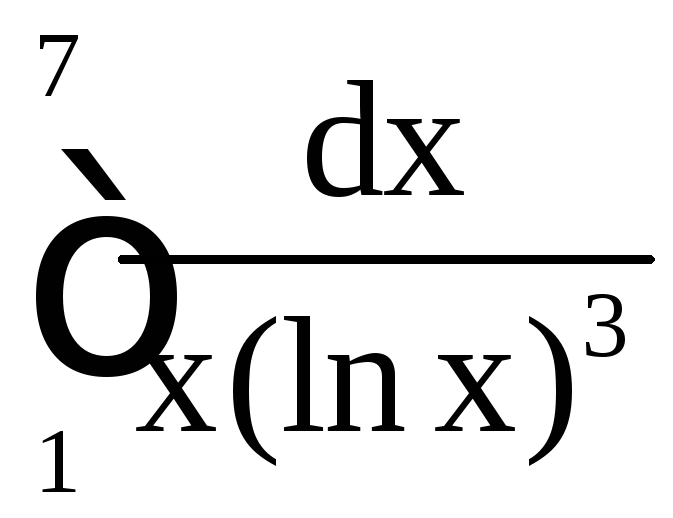 ;
28.
;
28. ;
;
21.
 ;
25.
;
25. ;
29.
;
29. ;
;
22.
 ;
26.
;
26. ; 30.
; 30. .
.
Задание 7.17
Исследуйте на сходимость несобственные интегралы.
1. а)
 , б)
, б) , в)
, в) ;
;
2. а)
 , б)
, б) , в)
, в) ;
;
3. а)
 , б)
, б) , в)
, в) ;
;
4. а)
 , б)
, б) , в)
, в) ;
;
5. а)
 , б)
, б) , в)
, в) ;
;
6. а)
 , б)
, б) , в)
, в) ;
;
7. а)
 ,
б)
,
б)
 , в)
, в) ;
;
8. а)
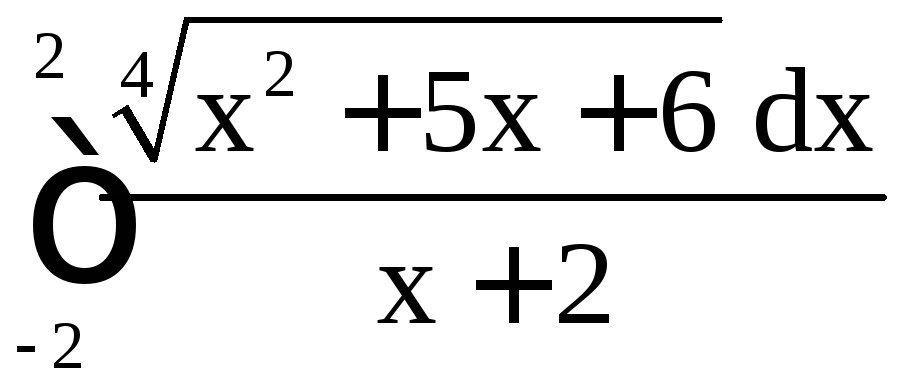 , б)
, б) , в)
, в) ;
;
9. а)
 , б)
, б) , в)
, в) ;
;
10. а)
 , б)
, б) , в)
, в) ;
;
11. а)
 , б)
, б) , в)
, в) ;
;
12. а)
 ,
б)
,
б) , в)
, в) ;
;
13. а)
 ,
б)
,
б) ,
в)
,
в) ;
;
14. а)
 ,
б)
,
б) ,
в)
,
в) ;
;
15. а)
 ,
б)
,
б) ,
в)
,
в) ;
;
16. а)
 ,
б)
,
б) , в)
, в) ;
;
17. а)
 ,
б)
,
б) , в)
, в) ;
;
18. а)
 ,
б)
,
б)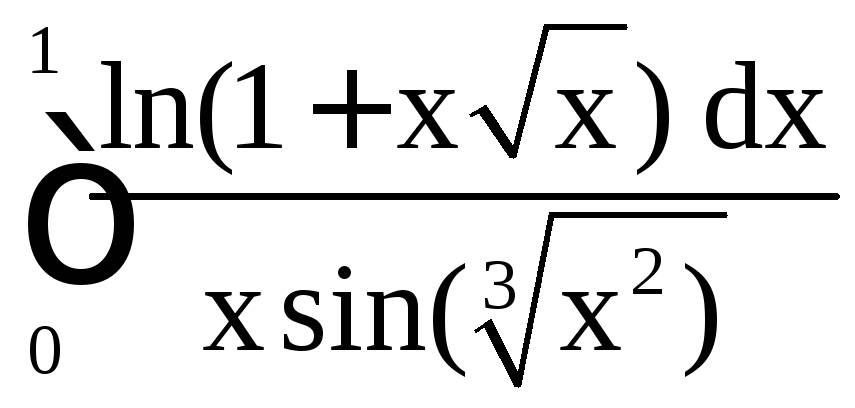 ,
в)
,
в) ;
;
19. а)
 , б)
, б) ,
в)
,
в)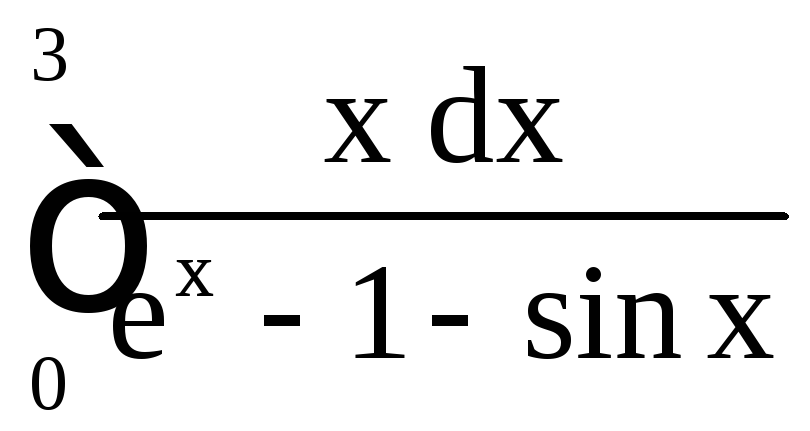 ;
;
20. а)
 , б)
, б) ,
в)
,
в) ;
;
21. а)
 , б)
, б) ,
в)
,
в) ;
;
22. а)
 , б)
, б) ,
в)
,
в) ;
;
23. а)
 , б)
, б) ,
в)
,
в)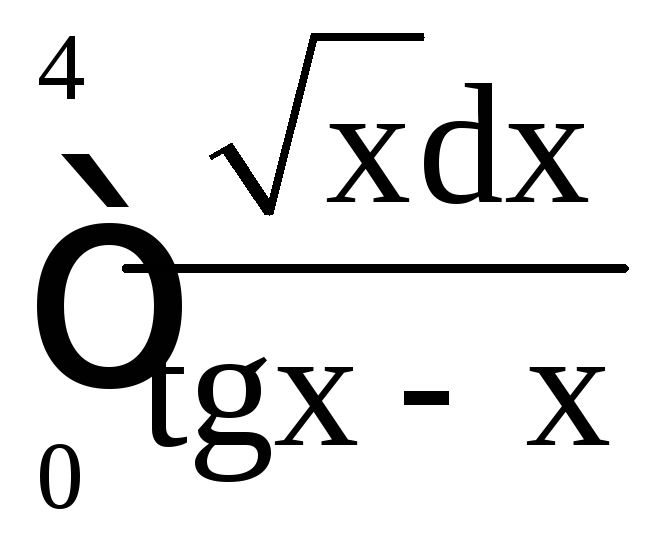 ;
;
24. а)
 , б)
, б) ,
в)
,
в) ;
;
25. а)
 , б)
, б) ,
в)
,
в) ;
;
26. а)
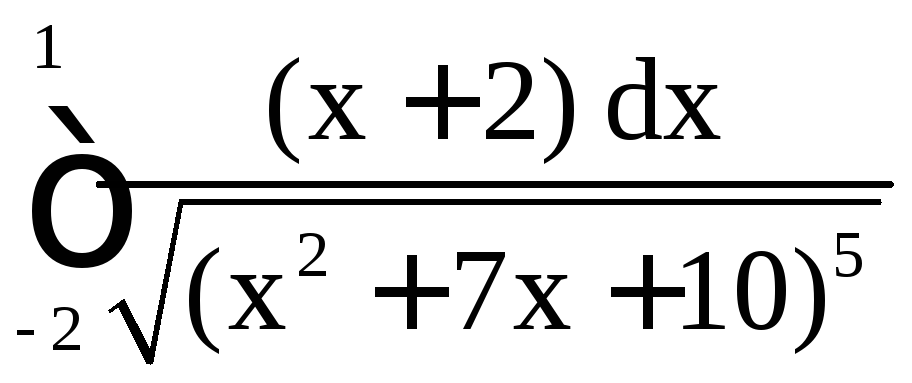 , б)
, б) ,
в)
,
в)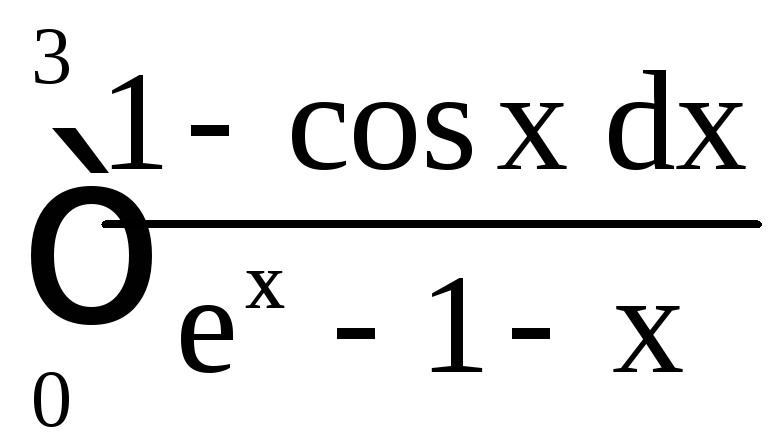 ;
;
27. а)
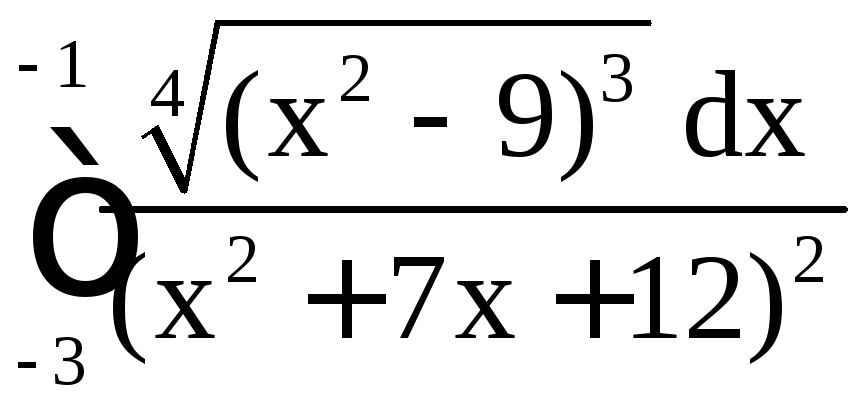 , б)
, б) ,
в)
,
в) ;
;
28. а)
 , б)
, б) ,
в)
,
в) ;
;
29. а)
 , б)
, б) ,
в)
,
в)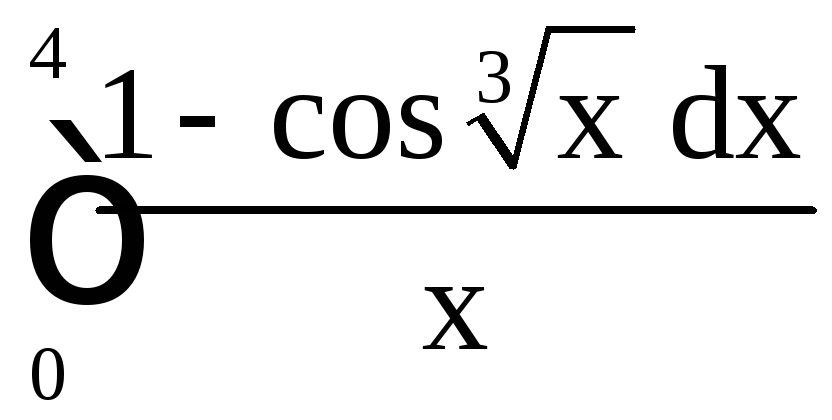 ;
;
30. а)
 , б)
, б) ,
в)
,
в) .
.
Задание 7.18
Найдите площадь фигуры, ограниченной линиями.
1.
![]() ,
,![]() ;16.
;16.
![]() ,
,![]() ;
;
2.
![]() ,
,![]() ;17.
;17.
![]() ,
,![]() ;
;
3.
![]() ,
,![]() ; 18.
; 18.
![]() ,
,![]() ;
;
4.
![]() ,
,![]() ; 19.
; 19.
![]() ,
,![]() ;
;
5.
![]() ,
,![]() ;20.
;20.
![]() ,
,![]() ;
;
6.
![]() ,
,![]() ;21.
;21.
![]() ,
,![]() ;
;
7.
![]() ,
,![]() ;22.
;22.
![]() ,
,![]() ;
;
8.
![]() ,
,![]() ;23.
;23.
![]() ,
,![]() ;
;
9.
![]() ,
,![]() ;
24.
;
24.
![]() ,
,![]() ;
;
10.
![]() ,
,![]() ; 25.
; 25.![]() ,
,![]() ;
;
11.
![]() ,
,![]() ; 26.
; 26.![]() ,
,![]() ;
;
12.
![]() ,
,![]() ; 27.
; 27.![]() ,
,![]() ;
;
13.
![]() ,
,![]() ; 28.
; 28.![]() ,
,![]() ;
;
14.
![]() ,
,![]() ; 29.
; 29.![]() ,
,![]() ;
;
15.
![]() ,
,![]() ; 30.
; 30.![]() ,
,![]() .
.
Задание 7.19
Найдите площадь фигуры, ограниченной линией, заданной в полярной системе координат указанным уравнением. Сделайте рисунок.
1. = 3sin3; 9. = –3cos2;
2. = 2sin4; 10. = 3cos4;
3. = –2sin3; 11. = –4cos2;
4. = –4sin2; 12. = 4cos3;
5. = –3sin3; 13. = 4sin2;
6. = 3cos2; 14. = –2cos2;
7. = –3sin2; 15. = –4cos4;
8. = 2sin2; 16. = –4sin4;
17. = –3cos3; 24. = –2sin4;
18. = 2sin3; 25. = 4sin4;
19. = 2cos2; 26. = 4cos2;
20. = –2sin2; 27. = 3sin2;
21. = –3cos4; 28. = 4cos4;
22. = –2cos3; 29. = –3sin4;
23. = 2cos4; 30. = –4cos3.
Задание 7.20
Найдите длину дуги кривой, заданной указанными уравнениями.
1. x = e-2tcos3t, y = e-2tsin3t, 0 t 6;
2. x = 4(t – sint), y = 4(1 – cost), 0 t 2;
3. x = 3(cost + tsint), y = 3(sint – tcost), 0 t 3;
4. x = e2tsin4t, y = e2tcos4t, 0 t 8;
5. x = (t2 – 2) sint + 2tcost, y = (2 – t2) cost+2tsint, 0 t ;
6. x = 3(1 – sint), y = 3(t – cost), 0 t 2;
7. x = e4tcos2t, y = e4tsin2t, 0 t 6;
8. x = 8cos3t, y = 8sin3t, 0 t 6;
9. x = 3(2cost – cos2t), y = 3(2sint – sin2t), 0 t 2;
10. x = e3tsin2t, y = e3tcos2t, 0 t 4;
11. x = et(cost + sint), y = et(cost – sint), 0 t 2;
12. x = 4(2cos2t – cos4t), y = 4(2sin2t – sin4t), 4 t 2;
13. x = e-4tcos3t, y = e-4tsin3t, 0 t 12;
14. x = 1 – cos3t, y = t – sin3t, 0 t 6;
15. x = 5(3sin2t – 2sin3t), y = 5(3cos2t – 2cos3t), 0 t 2;
16. x = e-tcos4t, y = e-tsin4t, 0 t 8;
17. x = (t2 – 2)sint + 2tcost, y = (2 – t2)cost + 2tsint, 0 t 2;
18. x = 2(t – sint), y = 2(1 – cost), 0 t 2;
19. x = 6(4cost – cos4t), y = 6(4sint – sin4t), 0 t 6;
20. x = e-3tsin2t, y = e-3tcos2t, 0 t 2;
21. x = 3(t – cos3t), y = 3(1 – sin3t), 0 t 2;
22. x = 5(cos4t – 2cos2t), y = 5(sin4t – 2sin2t), 0 t 2;
23. x = etsin5t, y = etcos5t, 0 t 10;
24. x = e4tcos2t, y = e4tsin2t, 0 t 6;
25. x = 8sint + 6cost, y = 6sint – 8cost, 0 t 2;
26. x = 7(3sint – sin3t), y = 7(3cost – cos3t), t 3 2;
27. x = 4(1 – cos2t), y = 4(t – sin2t), 0 t 2;
28. x = e-3tcos4t, y = e-3tsin4t, 0 t 8;
29.
![]() ,
,![]() ,
0
t
/4;
,
0
t
/4;
30. x = 4(3cos2t – cos6t), y = 4(3sin2t – sin6t), 0 t 2.
