
- •VII. Интегральное исчисление функции одного переменного
- •1. Неопределённый интеграл
- •2. Таблица основных неопределённых интегралов
- •3. Основные свойства неопределённого интеграла
- •4. Интегрирование методом замены переменного
- •5. Интегрирование по частям
- •6. Интегрирование рациональных функций Интегрирование рациональной функции
- •7. Интегрирование тригонометрических функций
- •8. Интегрирование некоторых иррациональных функций
- •9. Определённый интеграл
- •10. Несобственные интегралы
- •11. Вычисление площадей плоских фигур
- •12. Вычисление длины дуги
- •13. Вычисление объёмов тел
- •14. Приближённое вычисление определённых интегралов
- •Задание 7.1
- •Задание 7.2
- •Задание 7.3
- •Задание 7.4
- •Задание 7.5
- •Задание 7.6
- •Задание 7.7
- •Задание 7.8
- •Задание 7.13
- •Задание 7.14
- •Задание 7.15
- •Задание 7.16
- •Задание 7.17
- •Задание 7.18
- •Задание 7.19
- •Задание 7.20
- •Задание 7.21
- •Задание 7.22
11. Вычисление площадей плоских фигур
Площадь
криволинейной трапеции, ограниченной
графиками функций x
= a,
x
= b,
y
= 0, y
= f(x)
(f(x)
0 при x
[a;
b]),
находится по формуле
 .
.

Если фигура (D)
ограничена графиками функций x = a, x =
b, y = f(x), y = g(x), f(x)
g(x) при x
[a; b], то площадь S фигуры (D) находится по
формуле
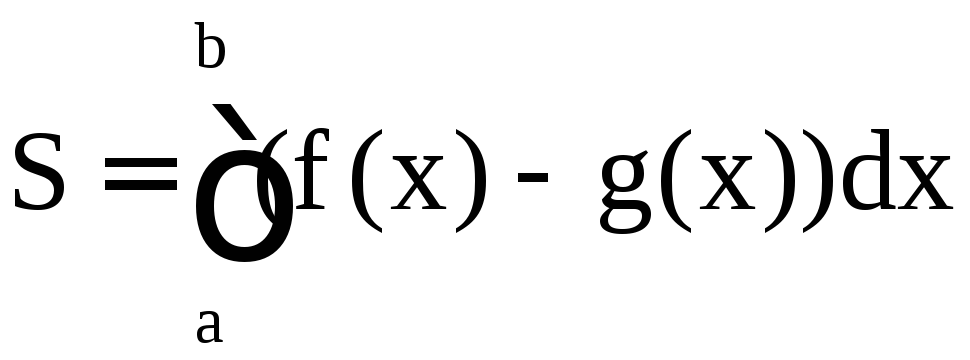 .
.


Пример 23. Найти площадь S фигуры (D), ограниченной линиями y = –x2 + 2x + 2 и y = 2x + 1.
Решение. Найдём абсциссы точек пересечения графиков функций, для чего решим уравнение: –x2 + 2x + 2 = 2x + 1; x2 – 1 = 0; x1 = –1,
x2 = 1. Для всех точек x из отрезка [–1; 1] –x2 + 2x + 2 2x + 1. Поэтому

 .
.
П ример 24.
Найти площадь фигуры, ограниченной
эллипсом
ример 24.
Найти площадь фигуры, ограниченной
эллипсом
 .
.
Решение.
Эллипс имеет две оси симметрии:
координатные оси 0х и 0у. Поэтому площадь
S фигуры равна учетверённой площади S1
части (D1)
фигуры, расположенной в первой четверти
(заштриховано). Фигура (D1)
ограничена сверху линией
 ,
снизу – осью 0х, слева – осью 0у. Поэтому
,
снизу – осью 0х, слева – осью 0у. Поэтому



 .
.
Отсюда находим S = 4S1 = ab.
Площадь S
криволинейного сектора, ограниченного
графиком функции
![]() и лучами
и лучами![]() и
и![]() в полярной системе координат, находится
по формуле
в полярной системе координат, находится
по формуле .
.
Пример 25.
Найти площадь S фигуры, ограниченной
линией, заданной в полярной системе
координат уравнением
![]() .
.
Решение.
Начнём с изображения линии. Так как
![]() ,
то нам нужно сначала решить неравенство
,
то нам нужно сначала решить неравенство![]() .
Имеем
.
Имеем

 ,
,
![]()
 ,
,
![]() .
.
При n = 0:
 ;
;
при n = 1:
 ;
;
при n = 2:
 ;
;
при n = 3:
 – этот угол является повторением угла,
соответствующего значению n = 0. Рассмотрение
других значений приводит к уже полученным
углам на плоскости. Рассмотрим рисунок.
Наша фигура ограничена тремя лепестками.
Её площадь S равна 3S1,
где S1
– площадь одного лепестка (заштриховано).
– этот угол является повторением угла,
соответствующего значению n = 0. Рассмотрение
других значений приводит к уже полученным
углам на плоскости. Рассмотрим рисунок.
Наша фигура ограничена тремя лепестками.
Её площадь S равна 3S1,
где S1
– площадь одного лепестка (заштриховано).
Имеем

 .
.
Отсюда находим S = 3S1= .
12. Вычисление длины дуги
Линия (L) в пространстве называется гладкой, если в каждой точке (L) можно провести касательную к этой линии. Если линия без самопересечений задана параметрическими уравнениями

то
дифференцируемость x(t),
y(t),
z(t)
гарантирует гладкость линии; аналогичное
утверждение справедливо для плоской
линии. Если линия без самопересечений
на плоскости с заданной полярной системой
координат определена полярным уравнением
![]() ,
то и в этом случае дифференцируемость
,
то и в этом случае дифференцируемость![]() влечёт гладкость этой линии.
влечёт гладкость этой линии.
Если гладкая линия
(L) на плоскости (в пространстве) задана
параметрическими уравнениями
![]() ,
,![]() (и вдобавок к этому
(и вдобавок к этому![]() для линии в пространстве),
для линии в пространстве),![]() ,
то длина
,
то длина![]() линии (L) находится по формуле
линии (L) находится по формуле
 (
( ).
).
Если гладкая линия
(L) задана явным уравнением
![]() ,
,![]() ,
то
,
то .
.
Для гладкой линии
(L), заданной полярными уравнениями,
![]() ,
, .
.
Пример 26.
Найти длину
![]() линии, заданной уравнением
линии, заданной уравнением![]() ,
,![]() ,
,![]() .
.
Решение.
Имеем



 .
.
Пример
27. Найти
длину дуги логарифмической спирали
![]() ,
находящейся внутри окружности
,
находящейся внутри окружности![]() .
.
Решение. Дуге
спирали, лежащей внутри окружности
![]() ,
соответствуют значения
,
соответствуют значения![]() .
Поэтому
.
Поэтому


 .
.
13. Вычисление объёмов тел
 Если
в пространстве заданы ось 0х, тело (Т),
проекцией которого на 0х является отрезок
[a; b] , и для любого x
[a; b] известна площадь S(x) поперечного
сечения S(x), то объём V тела (Т) находится
по формуле
Если
в пространстве заданы ось 0х, тело (Т),
проекцией которого на 0х является отрезок
[a; b] , и для любого x
[a; b] известна площадь S(x) поперечного
сечения S(x), то объём V тела (Т) находится
по формуле
 .
.
В частности, если
тело (Т) получено путём вращения графика
функции
![]() ,
,![]() вокруг оси 0х, то объём тела вращения
равен
вокруг оси 0х, то объём тела вращения
равен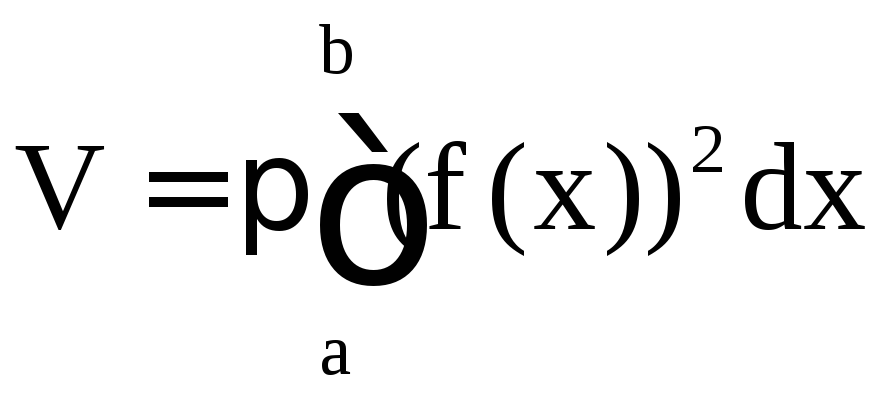 .
.
При вращении графика функции f(x) вокруг оси 0у формула объёма принимает вид
 .
.
Пример 28. Найти объём V тела (Т), ограниченного эллипсоидом
 .
.
Решение. Проекцией тела (Т) на ось 0х является отрезок [–a; a]. Найдём формулу площади S(x) поперечного сечения,
x [a; b]. Перепишем уравнение эллипсоида в виде
 .
.
Это есть уравнение
поперечного сечения эллипсоида
плоскостью, проходящей через точку x и
перпендикулярной оси 0х. А мы уже знаем
(задача 22), что площадь фигуры, заключённой
внутри этого эллипса, равна
 .
Следовательно,
.
Следовательно,


 .
.
