5. Элементарные преобразования графиков
Напомним некоторые
приемы, которые часто используются при
построении графиков функций. Пусть
построен график функции
.
Тогда:
1) график функции
получается из графика функции
переносом вдоль оси 0X на a единиц влево,
если
,
или на
единиц вправо, если
;
2) график функции
получается из графика функции
переносом на b единиц вверх, если b > 0,
или на
единиц вниз, если
;
3) график функции
получается из графика функции
сжатием вдоль оси 0X в
раз, если
,
или растяжением в
раз, если
;
4) график функции
получается из графика функции
растяжением вдоль оси 0Y в c раз, если
(при
сжатием в
раз);
5) графики функций
и
симметричны относительно оси 0Y; графики
функций
и
симметричны относительно оси 0X.
Пример 6.
Построить график функции
а б
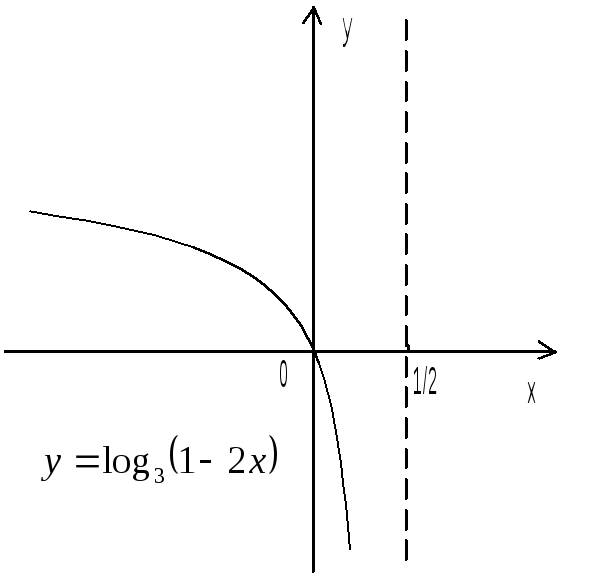
в г
Подчеркнем, что
величина сдвига вдоль оси
определяется
той постоянной, которая прибавляется
непосредственно к аргументу
,
а не к аргументу
.
Поэтому для нахождения этой постоянной
функцию
преобразуют к виду
.
Здесь сдвиг вдоль оси
на
единиц.
Например,
.
Значит, график функции
получается из графика функции
переносом вдоль оси
на
единиц вправо.
Пример 7. Построить график функции
.
а
б
в
г
Отметим также
следующее. Пусть заданы функция
и ее график. Тогда выражения
,
и
определяются следующим образом:
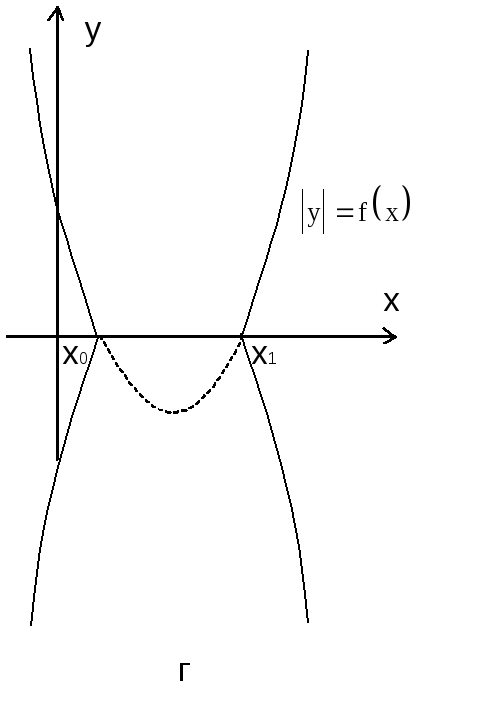
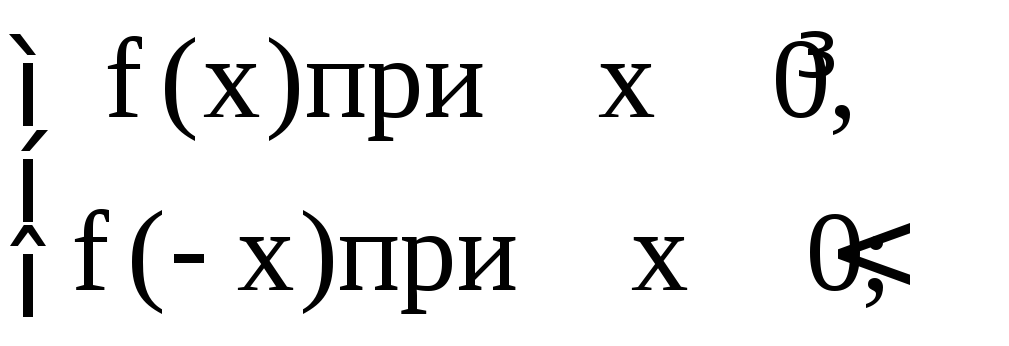
Графики этих функций приведены на рисунках, представленных ниже.
Задание 6.1
Для заданной функции f(x) = x4 + px3 + qx2 + rx +c и отрезка
[a; b] (коэффициенты приведены в таблице) найдите:
а) промежутки возрастания, убывания и точки экстремума;
б) наибольшие и наименьшие значения функции на отрезке [a; b].
|
№ варианта |
p |
q |
r |
c |
a |
b |
|
1 |
12 |
–8 |
–144 |
–5 |
–10 |
0 |
|
2 |
–8/3 |
–2 |
8 |
3 |
0 |
3 |
|
3 |
16/3 |
2 |
–24 |
1 |
–4 |
0 |
|
4 |
8/3 |
–10 |
–40 |
2 |
–2 |
3 |
|
5 |
–16/3 |
12 |
0 |
–1 |
–2 |
2 |
|
6 |
8/3 |
2 |
8 |
1 |
–3 |
1 |
|
7 |
32/3 |
–2 |
–32 |
–3 |
–3 |
1 |
|
8 |
–4/3 |
–12 |
0 |
5 |
–3 |
1 |
|
9 |
4 |
–8 |
–48 |
1 |
–4 |
1 |
|
10 |
4/3 |
–18 |
–36 |
2 |
–2 |
4 |
|
11 |
20/3 |
4 |
–32 |
–1 |
–3 |
2 |
|
12 |
–28/3 |
28 |
–8 |
3 |
0 |
3 |
|
13 |
20/3 |
–4 |
–40 |
–1 |
–3 |
3 |
|
14 |
16/3 |
–8 |
–64 |
2 |
–3 |
3 |
|
15 |
16/3 |
–18 |
–144 |
1 |
–4 |
1 |
|
16 |
4/3 |
–8 |
–16 |
–3 |
–3 |
1 |
|
Окончание таблицы | ||||||
|
№ варианта |
p |
q |
r |
c |
a |
b |
|
17 |
28/3 |
24 |
0 |
5 |
–3 |
1 |
|
18 |
–24/3 |
2 |
–24 |
1 |
0 |
4 |
|
19 |
4 |
–16 |
–96 |
0 |
–1 |
4 |
|
20 |
8/3 |
–18 |
–72 |
–1 |
–3 |
1 |
|
21 |
0 |
–26 |
48 |
6 |
–2 |
2 |
|
22 |
–6/3 |
5 |
0 |
5 |
–1 |
2 |
|
23 |
8 |
22 |
24 |
–1 |
–2 |
0 |
|
24 |
4 |
–2 |
–12 |
2 |
–2 |
2 |
|
25 |
0 |
–14 |
24 |
–3 |
–3 |
0 |
|
26 |
–4/3 |
–20 |
40 |
1 |
–3 |
1 |
|
27 |
–8/3 |
–10 |
24 |
–2 |
–2 |
2 |
|
28 |
–20/3 |
12 |
0 |
3 |
–1 |
1 |
|
29 |
–4/3 |
–8 |
16 |
–4 |
0 |
3 |
|
30 |
–4/3 |
–4 |
0 |
–5 |
–2 |
1 |