Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Инженерно-технологическая академия ЮФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

UML_4256

.pdf

Скачиваний:

Добавлен:

01.06.2015

Размер:

6.64 Mб

Скачать

☆

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 5018 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

M	y

a x ′0

0 x

''0

b x

Аналогично, если

f (x0′) − f (x) ≤ 0 x O(x0′,δ) ,

(3)

то в точке

x0′ функция достигает локального минимума.

Локальные

максимум и минимум называются локальными экстремумами.

На рисунке

f (x0′), f (x0′′) – локальные минимумы,

f (x0 )

– локальный

максимум.

Теорема 2 (Ферма). Если функция y = f (x)

дифференцируема в

точке x0 и достигает в этой точке локального экстремума, то

f ′(x0 ) = 0 .

Доказательство. От противного. Если

f ′(x 0 ) > 0 ,

то согласно

теореме 1

функция в

точке

x 0

возастает,

то

есть

не

достигает

локального

экстремума.

Если

р f ′(x0 ) < 0, то убывает

также не

достигает экстремума. Получили противоречие. Теорема доказана.

Геометрически теорема Ферма означает,

что в точке ( x 0 , f ( x 0 ))

график функции f (x) имеет горизонтальную касательную.

§2. Теоремы о среднем

Теорема 1 (Ролль). Если функция y = f (x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b), а на концах отрезка принимает равные значения ( f (a) = f (b)), то существует, по крайней мере, одна точка ξ (a,b), в которой f ′(ξ )= 0.

Доказательство. Так как функция f (x) непрерывна на отрезке [a,b], то, согласно второй теореме Вейерштрасса (см. §10 гл. 4), она

достигает на нём своего наименьшего m = inf f (x) и наибольшего M = sup f (x) значений.

Возможны два случая:

171

а) m = M. f (x)	′
	– const, следовательно, f (x) = 0 Теорема
доказана.	f (a) = f (b) , то, по крайней мере, одно из чисел
б) m ≠ M . Так как

m или M отлично от f (a).

Допустим M ≠ f (a) . Тогда M = f (ξ), где ξ (a,b). Это означает, что функция f (x) достигает в точке x = ξ локального максимума. По теореме Ферма f ′(ξ )= 0 . Что и требовалось доказать.

Геометрически теорема Ролля означает, что между двумя точками,

вкоторых значения функции равны, всегда найдётся точка, касательная

вкоторой параллельна оси 0 X .

Следствие. Если функция непрерывна на [a,b], дифференцируема

′	x (a,b),	то	f (a) ≠ f (b) . Доказательство от
на (a,b) , но f (x) ≠ 0
противного.
Теорема 2 (Коши). Если функции f (x)					и g(x) непрерывны на
[a,b], дифференцируемы на (a,b)		, причем			′	x (a,b) , то
					g (x) ≠ 0
существует точка ξ (a,b) такая, что			′
	f (b) − f (a)
		=	f (ξ)	.			(1)
	g(b) − g(a)		′
			g (ξ)
Доказательство.	Составим		вспомогательную				функцию
F(x) = f (x) +λg(x), где λ – некоторый коэффициент.						Подберём его

так, чтобы функция F(x) удовлетворяла условиям теоремы Ролля, то есть потребуем равенства на концах отрезка (F(a) = F(b)), так как все другие требования теоремы Ролля выполняются).

f (a) +λg(a) = f (b) +λg(b). λ =	f (b) − f (a)	.	(2)

	g(a) − g(b)

(g(a) ≠ g(b) согласно следствию теоремы Ролля).

Итак, если коэффициент λ		определяется формулой (2), то
функция F(x) удовлетворяет теореме Ролля, то есть
	F′(ξ )= 0, ξ (a,b).
Или		′		f (b) − f (a)
′	′
		f (ξ)
f (ξ) + λg (ξ) = 0.			−λ =		.
		′		g(b) − g(a)
		g (ξ)

Теорема доказана.

172

Теорема 3 (Лагранж). Если функция отрезке[a,b] и дифференцируема на интервале точка ξ (a,b) такая, что

f (b) − f (a) = f ′(ξ)(b −a).

		м0	В
			α
	А
0	a	ξ	b	x

f (x) непрерывна на (a,b), то существует

(3)

Доказательство. Положив в теореме Коши g(x) = x, получим

f (b)− f (a)

f ′(ξ ) или f (b) − f (a) = f ′(ξ )(b − a).

b − a

Теорема доказана.

f (b)− f (a)

Из рис. видно,

что

= tgα, где α – угол наклона секущей

AB , а из

b −a

f ′(ξ )= tgα , то есть теорема

(3)

видно, что

Лагранжа

утверждает, что между точками

A и B кривой существует точка М0

такая, что касательная в этой точке параллельна секущей.

Замечание. Пусть y = f (x) удовлетворяет теореме Лагранжа и

пусть [x0 , x0 + ∆x] [a,b]. Тогда согласно (3)

f (x + ∆x)− f (x )= f ′(ξ )∆x

или

∆y = f

′

(ξ )∆x , ξ (x0 , x0 + ∆x).

′

(3 )

Или

∆y = f

′

(x0 +θ∆x)∆x,

где 0 <θ <1. Равенства

′

(3 ) и (3)

называют формулой конечных приращений. Формула (3′) – это точное

равенство для любых конечных ∆x (в отличие от приближённого

∆y ≈ f ′(x0 )∆x ).

Во всех трёх теоремах речь идёт о существовании некоторой средней точки ξ (a,b), поэтому эти теоремы и называют теоремами о

среднем.

173

§3. Некоторые следствия из теоремы Лагранжа. Теорема Дарбу

Теорема 1. Пусть функция f (x) дифференцируема на интервале (a,b) . Тогда:

		′
а) если f (x) ≤ 0 x (a,b), то функция монотонно убывает;
б) если	f ′(x)= 0			x (a,b), то f (x) = const ;
в) если		′		x (a,b), то функция монотонно возрастает.
	f (x) ≥ 0
Доказательство.				Пусть a < x1,		x2 < b ,		x1, x2 – произвольные
точки. Тогда на отрезке [x1, x2 ] функция							f (x)	удовлетворяет теореме
Лагранжа.			f (x )− f (x ) = f ′(ξ )(x − x ),					ξ (a,b).	(*)

			2	1		2	1
Если	f	′	(x)≤ 0	x (a,b),	то		′	0 и из (*) следует
						f (ξ) ≤
f (x2 )≤ f (x1 ), то есть функция					f (x)	убывает монотонно на			(a,b).
Утверждение а) теоремы 1 доказано.
Утверждения б) и в) доказываются аналогично.
Теорема 2 (Дарбу). Пусть функция							f (x)	дифференцируемая на


[a,b]	и пусть λ ( f ′(a), f ′(b))			. Тогда найдётся точка ξ (a,b) такая,
что	f ′(ξ ) = λ ,	то есть функция		f ′(x) подобно непрерывной функции
принимает все свои промежуточные значения между f ′(a) и f ′(b).
	Доказательство. Пусть		f ′(a)< λ < f ′(b) (если				f ′(a) > f ′(b) –
доказательство		аналогично).	Положим c =		1	(a + b)	и введём	две

функции				2
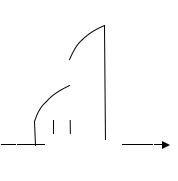
		α (t )= a и β (t )= 2t − a , если a ≤ t ≤ c .						(1)

		α (t )= 2t −b и β (t )= b, если c ≤ t ≤ b.						(2)

b β(t)

α(t)

0	a	c	b t

174

Тогда
a ≤α (t )< β (t )≤ b t (a,b)				(3)
(см. рис.). Рассмотрим сложную функцию
g(t) =	f (β (t )) − f (α (t ))	,	t (a,b).	(4)
	β (t )−α (t )

Очевидно, g(t) непрерывна на (a,b) как суперпозиция, разность и отношение непрерывных функций. Найдём предел

(1)

f (2t −a)− f

(a)

2t −a = x

lim g (t)=lim

2t −a −a

t→a

x → a

f (x) − f (a)

′

= lim

= f

(a).

x − a

x→a

(Производная f ′(a)

существует по условию теоремы).

Аналогично найдём

f (x)− f (b)

(2)

(b)− f (2t −b)

2t −b = x

lim g

(t ) = lim

= lim

= f ′(b).

x −b

t→b

b −(2b −t )

x → b

t→b

Доопределим функцию g(t) , положив

g(a) = lim g (t)= f ′

(a)

t→a

(b).

g(b) = lim g (t )= f ′

t→b

Тогда функция g(t)

будет непрерывной на отрезке [a,b] и по теореме

Коши (см. §11)

принимает все свои промежуточные значения, то есть

если

g(a) < λ < g(b),

или

f ′(a)< λ < f ′(b),

то найдётся точка t0 (a,b) такая, что

g(t0 ) = λ .

(5)

Зафиксируем t = t0 и из (4) найдём:

f (β (t0 ))− f (α (t0 ))= g (t0 )(β (t0 )−α (t0 )).

(6)

Но на отрезке

α(t ), β (t

) функция

f (x)

удовлетворяет

теореме

Лагранжа (см. теорему 3 §2)

f (β (t0 ))− f (α (t0 ))= f ′(ξ)(β (t0 )−α (t0 )), ξ (α (t0 ), β (t0 )). (7)

Сравнивая (6) и(7) , получим

175

g (t0 )= λ = f ′(ξ ).

Что и требовалось доказать.

Следствие. Если функция f (x) дифференцируема на отрезке [a,b], то её производная f ′(x) не имеет точек разрыва первого рода.

′

y(x)

y′η

y 0

			a		0 x0
			a		0 x0	B	x
						B
Доказательство.
Доказательство.		От		противного.			Пусть существует		функция
f (x), дифференцируемая			на [a,b], а её					′
f (x), дифференцируемая			на [a,b], а её					производная f (x) строго
возрастает на [a,b]	и имеет в точке x0 (a,b) разрыв первого рода (см.
рис.). Пусть			f ′(x0 − 0) = f ′(x0 ) = y0
			f ′(x0 − 0) = f ′(x0 ) = y0
и пусть					f ′(x0 + 0) = y1
и пусть					y0 <η < y1 .				(8)
					y0 <η < y1 .			f ′(x) примет	(8)
Согласно теореме			2		производная			f ′(x) примет	значение
η = f ′(x ), причём	x	> x	,	так как f ′(x)				строго возрастает. В силу
1	1	0

строгой монотонности

η = f ′(x1 ) > y1.

Получили противоречие (см. (8)). Это противоречие и доказывает следствие.

§4. Правило Лопиталя раскрытия неопределённостей

Теорема (Лопиталь). Пусть функции		f (x) и g(x)		определены и
дифференцируемы в некоторой	окрестности		точки	x = x0 ,	за
исключением быть может самой	точки	x = x0 .	Пусть	g′(x)≠ 0	в

окрестности точки x0 ,
lim	f (x)= lim g (x)= 0.
x→x0	x→x0
	176

Тогда, если существует (конечный или бесконечный) предел

lim

f ′(x)

(1)

g′(x)

x→x0

то существует равный ему предел lim

f (x)

то есть

g(x)

x→x0

lim

f (x)

= lim

f ′(x)

(2)

g(x)

x→x0

g′(x)

Доказательство. Если функции

f (x) и g(x) не определены в

точке x = x0 , то доопределим их равенствами

f (x0 )= lim f (x)= 0,

g(x0 ) = lim g(x) = 0.

→x0

x→x0

Пусть xn – произвольная точка из окрестности точки x0 . Тогда на

отрезке [x0 , xn ] функции

f (x) и g(x) удовлетворяют теореме Коши.

f (x

)− f (x

)

f (x

)

′(ξ

)

(x , x ).

(3)

g (xn )− g(x0 )

g (xn )

g′(ξn )

0 n

Пусть xn → x0 при n → ∞. Тогда ξn → x0

при n → ∞.

Поскольку

предел (1) существует, то не зависит от выбора последовательности, сходящейся к точке x0 , то есть

lim	f ′(ξn )	= lim	f ′(x)	.
	g′(ξn )		g′(x)
ξn →x0		x→x0

Перейдём к пределу в (3) при n → ∞. Так как предел правой части

(3) существует, то существует предел и левой части, то есть
lim	f (xn )	= lim	f (x)	= lim	f ′(x)	.
lim	g (x )	= lim	g(x)	= lim	g′(x)	.
xn →x0	g (x )	x→x0	g(x)	x→x0	g′(x)
	n

Теорема доказана.

Формулу (2) называют правилом Лопиталя раскрытия неопределённости вида 00 .

Замечание 1. Если f ′(x) и g′(x) удовлетворяют требованиям теоремы, то правило Лопиталя можно применить повторно.

177

ex − 1 x3 −

1 x2

− x −1

ex − 1 x2 − x −1

Пример 1. lim

= lim

−sin x + x

x→0

cos x +

−1

x→0

= lim

ex − x −1

= lim

ex −1

= lim

−cos x +

sin x

x→0

→0 cos x

Здесь правило Лопиталя применено четыре раза.

Замечание 2. Можно доказать, что правило Лопиталя применимо

и в том случае,

когда точка x0

–

бесконечно удалённая ( x0 = +∞ или

x0 = −∞).

−

sin x

cos x

= lim cos

Пример 2.

lim

= lim

=1.

x→∞

−

Замечание 3.

Правило

Лопиталя можно применить и для

раскрытия неопределённостей вида

∞.

nxn−1

∞

Пример 3.

lim

= lim

=K= lim

= 0.

xn = о(ex ) при

n → +∞.

x→∞ ex

x→∞

x→∞ ex

′(x)

Замечание 4. Если

lim

не существует, то это не означает,

x→∞ g′(x)

что не существует lim

f (x)

x→∞ g (x)

x +sin 2x

sin 2x

Пример 4.

lim

= lim

. Применим правило

cos

x→∞ 3x + cos x

x→∞

3 +

Лопиталя

x + sin 2x

1+ 2cos 2x

lim

= lim

x→∞ 3x + cos x

x→∞

3 −sin x

Этот предел не существует. Правило Лопиталя не применимо.

178

Замечание 5. Правило Лопиталя можно применить и для раскрытия неопределённостей вида 0·∞, ∞−∞, 1∞,00 ,∞0 , если

предварительно свести их к виду 00 или ∞∞.

Пример 5. Найти предел lim(ex + x)x .

x→0 1

Решение. Пусть u = (ex + x)x , тогда

ln u =

ln (ex

+ x)

Применим правило Лопиталя.

lim ln u = lim

ln (ex + x)

= lim

= 2.

+ x

x→0

x→0 ex

Используя непрерывность логарифмической функции, найдём

limlnu = ln

limu

)

= 2. limu = lim

ex + x

)

= e2.

x→0

(x→0

x→0

x→0 (

§5. Формула Тейлора для многочлена. Бином Ньютона

Рассмотрим многочлен n -й степени

xk .

(1)

P (x) = ∑ a

k =0

Представим этот многочлен следующим образом:

(x − x

= C

+ C (x − x

)+ C

(x − x )2

P (x)= ∑ C

k =0

(x − x )3

+K+ C

(x − x

)n .

(2)

Неизвестные коэффициенты Ck найдём следующим образом.

Продифференцируем (2) n раз. Получим

Pn′(x)= C1 + 2C2 (x − x 0 )+ 3C3 (x − x 0 )2 +K+ nCn (x − x 0 )n−1 ,

Pn′′(x)= 2C2 + 3 2C3 (x − x 0 )+K+ n(n −1)Cn (x − x 0 )n−2 ,

(3)

Pn′′′(x)= 3 2C3 +K+ n(n −1)(n − 2)Cn (x − x 0 )n−3 ,

…………………………………………………………….

P(n)n (x) = n!Cn .

179

Полагая в (2) и (3) x = x0 , найдём:

C0 = Pn (x0 ),C1 = Pn′(x0 ),C2 =

Pn′′(x0 ),

P′′′(x ), K ,C

P(n) (x

Ясно, что

P(k )

(x ).

(4)

Таким образом,

многочлен (2) примет вид

(5)

P (x)= ∑ 1

P(k ) (x )(x − x )k .

k =0

Многочлен (5) называют многочленом Тейлора. Его коэффициенты определяются соответствующей производной многочлена в точке x0 . Очевидно, что всякий многочлен является

многочленом Тейлора и задав значения многочлена и его n производных в некоторой точке, мы определим и сам многочлен.

Рассмотрим частный случай

P (x)

xk .

= (x + a)n = ∑ a

k =0

Коэффициенты ak найдём по формуле (4) при x0 = 0 .

ak =

((x + a)n )(k ) =

n(n −1)(n − 2)K(n − k +1)(x + a)n−k

x=0 = Cnk an−k .

Таким образом, мы получили формулу бинома Ньютона.

(x + a)n = ∑ Cnk xk an−k .

(6)

k =0

§6. Формула Тейлора для функции

Пусть функция

y = f (x)

дифференцируема n раз в окрестности

точки x0 . Запишем для неё многочлен Тейлора

Tn( x) = ∑

f (k )

(x0 )(x − x0 )k = f (x0 )+ f ′(x0 )(x − x0 )+

k =0 k!

f ′′(x0 )(x − x0 )2 +K+

f (n) (x0 )(x − x0 )n .

(1)

180

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 5018 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.09.2019687.71 Кб19Uchebnoe_posobie_metrologia.docx
#
01.06.20152.46 Mб17UMK_po_Menedzhmentu_modul_2.pdf
#
01.06.2015359.44 Кб8umk_treb.pdf
#
01.07.202586.88 Кб0UML диаграммы в Rational Rose_лаб1.docx
#
01.06.2015903.17 Кб15UML_1321.pdf
#
01.06.20156.64 Mб26UML_4256.pdf
#
01.06.2015321.05 Кб16UML_4497.pdf
#
01.06.20151.11 Mб9UML_4562.pdf
#
01.06.2015641 Кб10UML_4564.pdf
#
01.06.2015943.33 Кб10UML_4597.pdf
#
01.06.20151.72 Mб72UML_4797.pdf