UML_4256

Неизвестные коэффициенты di частного находятся из сравнения

n

коэффициентов при одинаковых степенях x ( an = ∑bn−1di , n = 0,1,2,...).

i=0

Теорема 2 (Мертенс). Если ряды ( A) и (B) сходятся, причем хотя бы один из них абсолютно, то их произведение, взятое в форме Коши (то есть ряд (C* )), сходится и его сумма равна AB (без доказательства).

Замечание. Условия теоремы 2 достаточные. Они не являются

u11 +u12 +u13 +... +u1k +...

+u21 +u22 +u23 +... +u2k +...

+...........................................

+ui1 +ui2 +ui3 +... + uik +...

называется двойным рядом.

Двойной ряд обозначают так:

Частичной суммой Smn ряда (11) называют сумму mn членов этого ряда

101

Докажем теперь, что метод Пуассона-Абеля линейный и регулярный. Линейность следует из линейности предела, через который он определяется. Регулярность примем без доказательства.

Рассмотрим теперь метод Чезаро суммирования расходящихся

∞

рядов. Под суммой ряда ∑ ak по Чезаро понимается предел средних

k =1

k

арифметических частичных сумм Sk = ∑ai этого ряда, то есть

i=1

∞

Пример 3. Найти сумму ряда ∑ (−1)n+1 .

n=1

0, k - четное, Решение. Так как Sk = 1, k - нечетное,

то

Воспользуемся формулой (6).

Итак, результат совпадает с результатом Пуассона-Абеля.

∞

Пример 4. Найти сумму ряда ∑ sin (nθ ).

Как видно, результаты опять совпадают.

Можно доказать, что если ряд суммируем по Чезаро, то он суммируем и по Пуассону-Абелю и их суммы совпадают.

Можно доказать, что метод Чезаро линейный и регулярный.

106

ГЛАВА 4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ

§1. Понятие функции. Основные элементарные функции

соответствие элемент y Y . Элемент y называется образом, а элемент

x – прообразом.

Если все элементы множества Y являются образами, то говорят об отображении X на Y (а не в Y ).

Отображение называется однозначным, если x X существует единственный y Y ( ! y Y ). Однозначное отображение называется

взаимно-однозначным, если каждому образу соответствует единственный прообраз.

Определение. Однозначное отображение множества X в множество Y называют функцией. Множество X называют областью определения функции, а множество образов G Y называют областью значений функции.

f

Пишут: f : X →Y ; f (X ) = G ; x→ y ; y = f (x). Если f (X ) = G , то X = f −1 (G) – прообраз образа G .

Если множества X и Y – конечные, то отношение (связь) между множествами можно наглядно изобразить в виде следующих графов

(см. рис.):

Граф 1 не является отображением.

Графы 3 и 5 являются отображением множества X в множество Y . 107

Графы 2, 4, 6 – отображения множества X на множестве Y . Графы 3, 4, 5, 6 являются однозначными отображениями X в Y , то

есть функциями.

Графы 5 и 6 взаимно-однозначные функции, а граф 6 – биекция. Если область определения функции y = f (x), X R1 и область

значений функции G R1 , то функцию называют действительной функцией одного действительного аргумента x . Если X R1 , а

G R2 , то функцию называют векторной функцией параметра x , или комплекснозначной функцией аргумента x .

вместо «функция» часто говорят «оператор». Например, оператор проектирования вектора на плоскость, оператор дифференцирования и прочие.

Если X – множество функций, а Y – числовое множество, то вместо «функция» говорят «функционал». Например, b∫ f (x)dx =ϕ( f ) –

Например, y = x2 , x X = R1 – функция одного аргумента. Ее график – парабола, то есть множество {(x, x2 )} R2 .

аргументов. Ее график – параболоид вращения, то есть множество упорядоченных троек

{(x, y, z)| z = x2 + y2} R3 .

108

z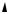

0 y

х

U = x2 + y2 + z2 , X = R3 – функция трех переменных. Ее график – гиперпараболоид, то есть множество {(x, y, z,u)| u = x2 + y2 + z2} R4 .

называется композицией (суперпозицией) отображений f и g . Пишут u = fog . Функцию u (x) называют сложной функцией аргумента x . Пишут u (x)= f (g (x)) или u = f (y), y = g (x).

y называют промежуточным аргументом, а x – независимым аргументом. Например, y = sin2 x3 – суперпозиция 3-х функций: y = u2

(степенная), u = sin t (тригонометрическая), t = x3 (степенная).

Если функции f и g заданы на одном и том же множестве X , то запись f = g (равенство функций) означает, что f (x) = g (x) x X .

Таким образом, в множестве функций мы ввели определение равенства функций. Сумму и разность функций f (x) и g (x) определим

равенством

def

u (x) = f (x)± g (x) x X .

Аналогично определим произведение и отношение функций v(x)= f (x)g (x) x X , w(x)= gf ((xx)) x X | g (x)≠ 0 .

Заметим, что, если функция задается аналитическим выражением (формулой), то область ее определения обычно не указывается, так как ее можно найти по виду этой формулы.

Следующие функции называют основными элементарными функциями:

109

1.y = xµ , µ R – степенная функция.

2.y = ax , a > 0 – показательная функция.

3.y = loga x, a > 0, a ≠1 – логарифмическая функция (обратная

функции.

Всякая функция, которая получается из основных элементарных функций путем конечного числа введенных выше арифметических операций и суперпозиций функций, называется элементарной.

Приведем примеры неэлементарных функций:

Однако некоторые свойства и теоремы мы будем формулировать в более общем виде, то есть для функций, определенных в некотором метрическом пространстве со значениями в другом метрическом пространстве.

110