3Л_Одномерная Оптимизация

Алгоритм деления интервала пополам

Это вариант алгоритма равномерного блочного поиска при n=3.

Схема алгоритма.

Шаг 1. Задаются a, b, . Производим эксперимент в точке x2=(a+b)/2, т.е. вычисляем y2=f(x2)

Шаг 2. Проводим эксперименты в остальных точках блока: x1=(a+x2)/2, y1=f(x1) и x3=(x2+b)/2, y3=f(x3).

Находим xj такую, что f(xj)=min {f(xi)}.

Следовательно, достигнутая точность будет ~ | , =1/2LN. x

*

x

|

Метод дихотомии

Это алгоритм блочного поиска для ni=n=2, т.е. когда в блоке два эксперимента. Метод дихотомии является самым естественным и наиболее распространенным на практике. Деление отрезка пополам производится так:

L2*2 = ½ (1/2 - /2) + /2 = ¼ + ¾

L2*3 = ½ ( ¼ - ¾ ) + /2 = 1/8 +7/8

После проведения k пар экспериментов получим отрезок неопределенности

L2 k=2-k + (1 – 2-k ) .

После проведения n экспериментов (n=2k) отрезок неопределенности будет равен

(без учета ) Ln=2-n\2.

Эффективность метода охарактеризуется величиной: (L0/Ln) = 2-n\2 .

Для получения интервала размера L при поиске методом дихотомии (половинным

делением) потребуется сделать

Пример решения задачи методом дихотомии

Значения функции в этих точках будут следующие:

у1=12х1-2х21=12*4.9-2*(4.9)2=11; у2=12х2-2х22=12*5.1-2*(5.1)2=29.

Интервал неопределенности сократился до L2=[0;5.1].

получаем у3=17.5, у4=17.8. Интервал неопределенности стал L4=[2.45;5.1].

Далее получаем х5=3.63, x6=3.83, y5>y6, L6=[2.45;3.85], откуда х7=3.05, х8=3.25; у7=18,

у8=17.8. Интервал неопределенности после четырех пар экспериментов сократился до L8*=[2.45;3.25], 18=0.8<1n.

В качестве решения принимаем ymax= y7=18. Этот максимум достигается в точке х=3.05. (Нетрудно убедится , что максимальное значение функции f(x) действительно равно 18 и достигается в точке х=3.)

Метод чисел Фибоначчи

Метод применяется, когда число экспериментов N заранее задано. Метод чисел Фибоначчи относится к симметричным методам, т.е. точки, в которых выполняются два эксперимента, на основе которых происходит уменьшение отрезка неопределённости, расположены симметрично относительно середины отрезка.

В результате экспериментов получается отрезок неопределённости [а,х2], содержащий

точку х1, или отрезок неопределённости [х1,в], содержащий точку х2. Остающаяся

точка делит новый отрезок неопределённости на две неравные части в пропорциях

определяемых числами Фибоначчи.

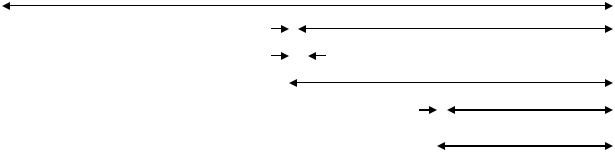
Схема расположения точек измерения по методу Фибоначчи

В результате проведения (n-2) измерений получен минимальный интервал

Ln 2, концы которого обозначим хн и хк. Внутри него в т. х’ находится эксперимент, при котором был получен наилучший результат из всех первых (n-2) испытаний.

Ln 2

Ln 1

Ln

Проделав (n-1)-й эксперимент в точке х’’, получим новый интервал неопределенности

(хн, х’’) или (х’, хк ) длиной Ln 1 . На этом отрезке окажется эксперимент с наибольшим значением функции, а последнее измерение х’’’ должно быть сделано так, чтобы длина последнего интервала Ln была независима от его исхода. Для этого должно выполняться условие

Алгоритм метода Фибоначчи

Шаг 1. По заданной ln точности рассчитывается вспомогательное число

N bk aн ln

Шаг 2. Для определения необходимого числа опытов n находится такое число

для i-го шага будет xi mFn j 2 в соответствии со

следующим правилом. Если при выполнении шага значение функции в точке

xi+1=xi+ xi оказывается больше, т.е. f(xi+1)>f(xi) (шаг удачный), то следующий (i+1)-й шаг выполняется из точки хi+1: xi+2=xi+1+ xi+1. Если i-й шаг неудачный, т.е. f(xi+1)<f(xi), то следующий (i+1)-й шаг выполняется из точки хi, т.е. xi+2=xi- xi+1.

Указанный процесс продолжается до тех пор, пока не будут исчерпаны все числа Фибоначчи в убывающей последовательности. Последний n-ий шаг выполняется посередине отрезка Ln-1 (методом половинного деления).

Пример решения задачи методом Фибоначчи

Пример 2. Необходимо найти максимум функции у=12х-2х2 методом Фибоначчи. Интервал точности положения максимума (максимально допустимый интервал неопределенности) 10=0.1L0. Отрезок, на котором задана функция L0=[0, 10]=10, где хн=0, хк=10. Минимально допустимый интервал неопределенности, соответствующий минимальному расстоянию между экспериментами, при котором они различны

ε=0.01.

Решение. В соответствии с алгоритмом найдем N= 10/1 = 10, F5<N<F6, откуда Fn= F6 =13,

n=6. Определим максимальный шаг поиска m xк xн 10 0.77.

Fn 13

Найдем точку х1 в которой вычисляется значение y1 : x1=хн+mFn-2=хн+ mF4 = 0+0.77*5 = 3.85; у1= 46-29.6 =16.4.

Найдем точку х2 : x2=x1+mFn-3= 3.85+0.77*3 = 6.42; у2=77-83=-6.

Поскольку y1>y2, получим L2=[0;6.42]. Так как f(x2)<f(x1) (шаг неудачный), то в соответствии с алгоритмом следующий шаг выполняется из точки х1 т.е.

х4=х3 – mFn-i-2 = x1 – mF6-2-2 = 3.85-0.77*2 = 2.31; у3=27.7-10.8=16.9. Поскольку y3>y1

получим L3=[0;3.85].

Так как y3>y1 (шаг удачный), то направление шага (знак приращения) не меняется и х4=х3 – mF1=2.31-0.77*1=1.54; у4=13.76. Поскольку у3>у4, то L4=[1.54;3.85].

Так как у4<у3 (шаг неудачный), то меняется направление шага:

х5=х3+mF0=2.31+0.77*1=3.1; у5=18. Поскольку у5>у3, то L5=[2.31;3.85].

Числа Фибоначчи исчерпаны и x6 находится с использованием метода половинного деления: x6 =(3.85+2.31+0.01)/2= 3.085; y5=17.99.

Ответ. В точке х=3.085 функция достигает максимума ymax = 17.99.

Метод золотого сечения

Метод используется когда требуется найти не собственно экстремум функции, а то значение параметров, при котором достигается некоторое условие, например f(x) Y, т.е заранее не возможно оценить необходимое число опытов

Метод золотого сечения, также как и метод Фибоначчи, относится к симметричным методам. Для уменьшения отрезка неопределённости [а,в], вычисляют значение целевой функции в двух точках отрезка. В результате этих экспериментов отрезок неопределённости сузится до отрезка [а,х2] или [х1,в]. Так как нет никаких оснований предпочесть один из этих вариантов, то точки х1 и х2 должны быть симметричны относительно середины отрезка [а,в], т.к. в этом случае длины отрезков [а,х2] и [х1,в] будут равны.

Этот метод, также как и метод Фибоначчи, требует выполнения условия

Lj-1= Lj + Lj+1 , где k=1,2,…n,

и предполагает постоянство отношений длин последовательных интервалов

Проведем эксперимент, выполняя одновременно эти два условия. Разделив первое условие на Lj , получим: 2- -1=0,

- это значение и обусловило название метода.

Схема положения точек исследования по методу золотого сечения

Вметоде золотого сечения точка х1 выбирается из соображения, что должно выполняться соотношение:

С - есть «золотое отношение». Точка х2 определяется как точка симметричная к х1 относительно середины отрезка.

В результате экспериментов получается отрезок неопределённости [а,х1], содержащий

точку х2, или отрезок неопределённости [х2,в], содержащий точку х1. Точка,

оставшаяся на суженном отрезке неопределённости, вновь делит его по правилу «золотого сечения». Следовательно, чтобы уменьшить новый отрезок неопределённости, необходимо вычислить значение целевой функции в точке, симметричной к оставшейся точке относительно середины этого нового отрезка.

Схема алгоритма метода золотого сечения