выявляется отклонение доли бракованных деталей от установленного процента брака меньше чем на 1%.

Решение. Воспользуемся формулой .

Здесь , , , .

Тогда .

Пример 2. Сколько нужно произвести измерений, чтобы с вероятностью равной 0,95 утверждать, что погрешность средней арифметической результатов этих измерений не превысит 0,1, если .

Решение. Воспользуемся формулой .

Здесь , .

Имеем , , .

12. Квантили случайных величин

Пусть непрерывная случайная величина имеет функцию распределения , плотность распределения и пусть задано число .

Определение. Квантилью уровня случайной величины называется такое число , что .

Рис. 4

Обозначим через квантиль уровня случайной величины ;

через – квантиль уровня распределения Пирсона с степенями свободы,  – квантиль уровня распределения Стьюдента с степенями свободы.

Свойства квантилей:

1) , ;

2) если квантиль уровня случайной величины , то ;

3) при ;

4) ;

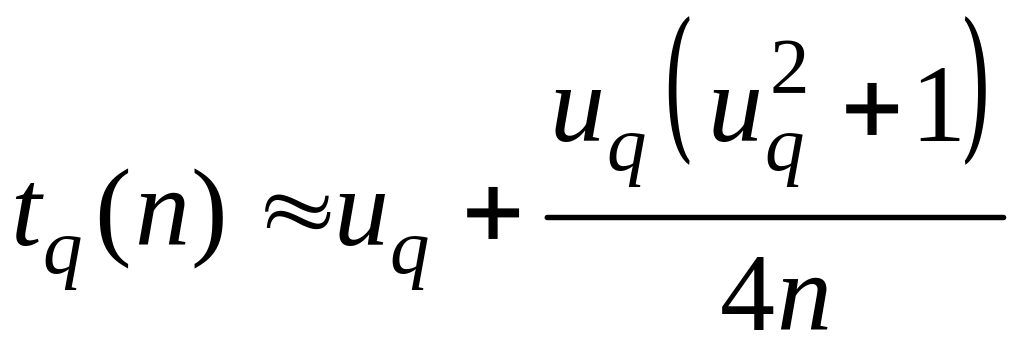
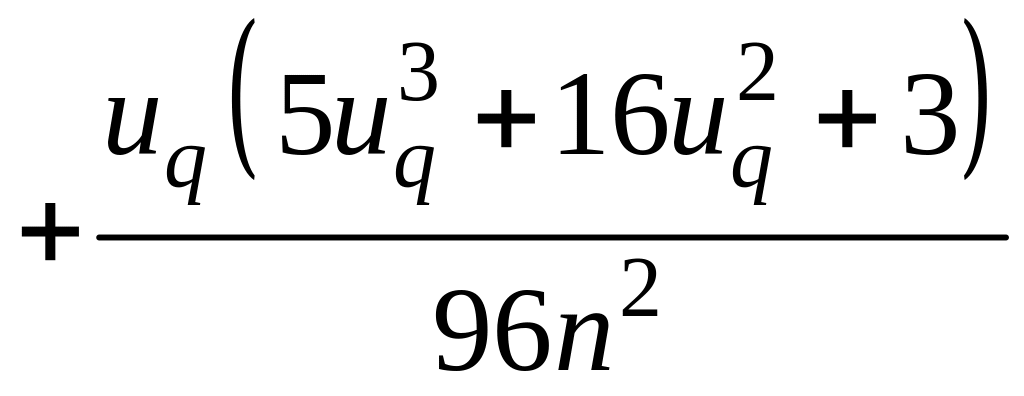
5) ;

6) для малых .

13. Точечные и интервальные оценки параметров распределения

Совокупность результатов измерений (2) случайной величины в математической статистике называется выборкой, при этом случайная величина называется генеральной совокупностью, а – объемом выборки.

Предположим, что функция распределения генеральной совокупности принадлежит к определенному классу функций, зависящих от одного или нескольких параметров .

Под точечной оценкой неизвестного параметра функции распределения генеральной совокупности понимают приближенное значение на основе выборки (2) ограниченного объема

. (3)

Заметим, что оцениваемый параметр есть число нам неизвестное, а его оценка (3) – случайная величина.

Оценка (3) называется:

1) несмещенной (без систематических ошибок), если .

2) состоятельной, если сходится к истинному значению параметра по вероятности, т.е.

.

3) несмещенная оценка называется эффективной, если у нее по сравнению с другими несмещенными оценками наименьшая дисперсия

.

Пусть – какая-либо точечная оценка неизвестного параметра и пусть найдено число такое, что выполняется равенство

. (4)

Равенство (4) означает, что интервал со случайными границами с вероятностью накрывает неизвестное истинное значение параметра .

При этом интервал называется доверительным интервалом, а вероятность – доверительной вероятностью (обычно выбирают ).

Примеры доверительных интервалов

1. Если генеральная совокупность распределена по нормальному закону и известно, то с вероятностью , где – квантиль уровня распределения , .

2. Если генеральная совокупность и неизвестно, то с вероятностью

, , ,

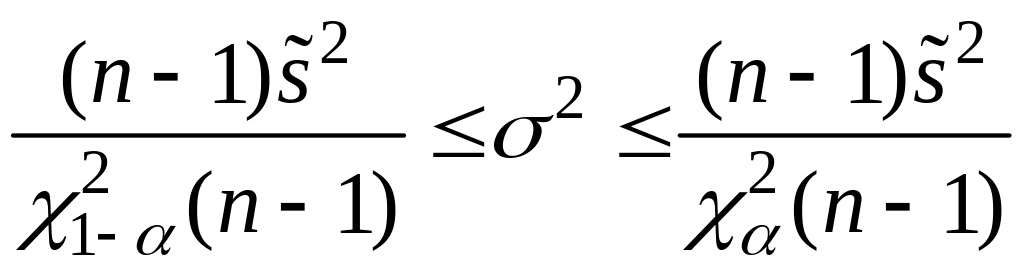где ,  – квантиль распределения Стьюдента (Пирсона) с степенью свободы уровня , – объем выборки (2).

3. Пусть производится серия из независимых испытаний, в каждом из которых событие может произойти с неизвестной вероятностью . В качестве точечной оценки вероятности возьмем частоту , где – объем выборки, а – количество испытаний, в которых событие произошло .

Тогда, если , , , то с вероятностью , где .

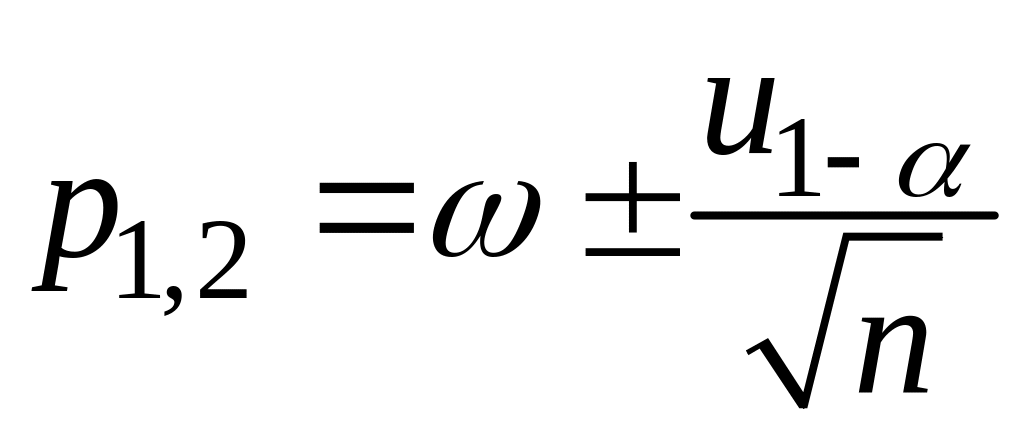
Или более точно

.

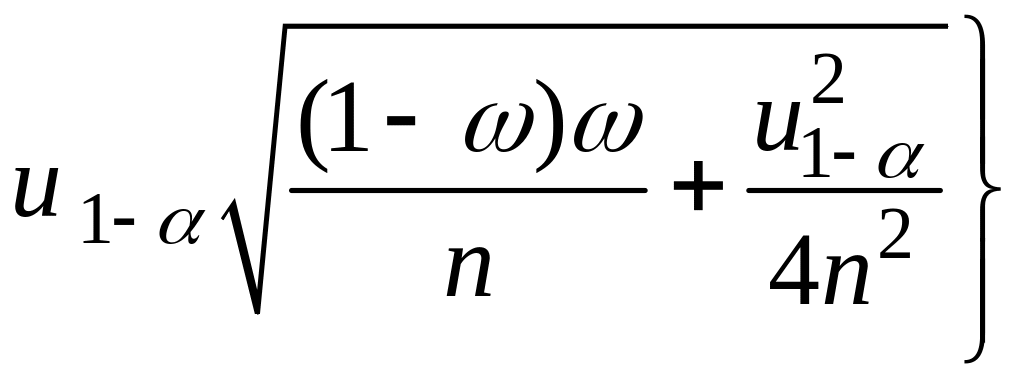14. Проверка статистических гипотез

Статистическими гипотезами называют любые предложения относительно параметров (такие гипотезы называют параметрическими) или вида функции распределения случайной величины.

Задача проверки статистической гипотезы относительно генеральной совокупности ставится так:

Найти правило, позволяющее по выборке (2) обоснованно решить вопрос о принятии или отклонении гипотезы . Для решения этой задачи выбирают критерий проверки, т.е. некоторую функцию от выборки

(5),

которая является случайной величиной, так как все есть случайные величины. Предполагается, что для этой функции известны плотности распределения вероятностей и , где – альтернативная гипотеза. Зададим уровень значимости . Эта вероятность такова, что событиями, происходящими с такой вероятностью в данной ситуации, можно пренебречь.

Критической областью называют совокупность значений критерия , при которой гипотезу отвергают.

Область находят из условия

. (6)

Отметим, что условием (6) область определяется неоднозначно.

Основной принцип проверки статистической гипотезы состоит в следующем: по выборке (2) и формуле (5) считают величину .

Если , то отвергают в пользу альтернативной гипотезы . Если же , то оснований отвергнуть нет, так как выборочные данные (2) не противоречат гипотезе .

Число называют мощностью критерия.

. (7)

При принятии или отклонении гипотезы возможны ошибки двоякого рода: 1) ошибка первого рода – отвергают, а она верна.

Вероятность ошибки 1 рода ;

2) ошибка второго рода – принимают, а она не верна.

Вероятность ошибки второго рода .

Из формулы (7) видно, что чем больше мощность , тем меньше ошибка 2 рода. Обычно поступают следующим образом: фиксируют уровень значимости , т.е. фиксируют приемлемую вероятность ошибки 1 рода, а затем ищут критерий с наибольшей мощностью, то есть с наименьшей ошибкой 2 рода.

Таким образом, проверка параметрической статистической гипотезы может быть разбита на следующие этапы:

1) формулируем гипотезы и ;

2) назначаем уровень значимости ;

3) выбираем статистику (5) для проверки гипотезы ;

4) находим плотности распределения и ;

5) в зависимости от гипотезы находим критическую область ;

6) по выборке (2) вычисляем ;

7) принимаем решение: если , гипотезу оставляем. Если , гипотезу отклоняем в пользу альтернативной .

Модель 1. Пусть известно, что генеральная совокупность ,  – известно. Требуется по выборке (2) и уровню значимости проверить нулевую гипотезу : .

Решение. Для этой модели статистика , где .

Тогда для альтернативной гипотезы

, критическая область ,

, ,

, .

Для простой альтернативной гипотезы

, мощность ;

Для гипотезы , , .

Здесь ,  – квантиль уровня случайной величины .

Модель 2. Пусть генеральная совокупность , но оба параметра неизвестны. По выборке (2) найдем точечные оценки

и

неизвестных параметров.

По уровню значимости проверить нулевую гипотезу :

Решение. Для альтернативных гипотез , критическая область .

, .

, ,

где ,  – квантиль уровня распределения Стьюдента с степенью свободы.

Для , , мощность ,

где – функция распределения Стьюдента с степенью свободы.

Модель 3. Пусть имеем две независимые выборки (2) и

(8)

объемом и из нормальных генеральных совокупностей и . Предположим, что и известны. Требуется на уровне значимости проверить гипотезу : :

Решение. Для этой модели статистика

,

где , .

Для альтернативных гипотез , область , область , , , где – квантиль уровня случайной величины .

Пример 1. По паспортным данным автомобильного двигателя расход топлива на 100 км пробега составляет 10 л. Ожидается, что после модернизации двигателя расход топлива уменьшится. Для проверки производятся испытания 25 случайно отобранных автомобилей с модернизированным двигателем. По результатам испытаний выборочная средняя расходов топлива на 100 км пробега составила л. Предполагая, что расход топлива есть нормальная случайная величина с проверить гипотезу , утверждающую, что изменение конструкции двигателя не повлияет на расход топлива при уровне значимости .

Решение. Дано: , , , , , .

Вычислим статистику .

Область , где квантиль уровня случайной величины . Имеем , т.е. .

Так как , то гипотезу отвергаем в пользу альтернативной. То есть из опытных данных следует, что модернизация двигателя привела к уменьшению расхода топлива.

Замечание. Пусть в условиях задачи . Вычислим мощность критерия , вероятность ошибки второго рода , и ответим на вопрос, какой минимальный объем выборки нужно взять, чтобы .

Имеем .

, где .

.

Решим уравнение

,

,

, , .

Пример 2. Из продукции двух станков-автоматов, выпускающих однотипные изделия, взяты выборки объемов и . По результатам выборок найдены мм, мм. Дисперсии генеральных совокупностей известны , . В предположении о нормальном законе распределения погрешностей изготовления требуется на уровне значимости проверить гипотезу при альтернативной гипотезе .

Решение. У нас , , , , , , .

Статистика .

.

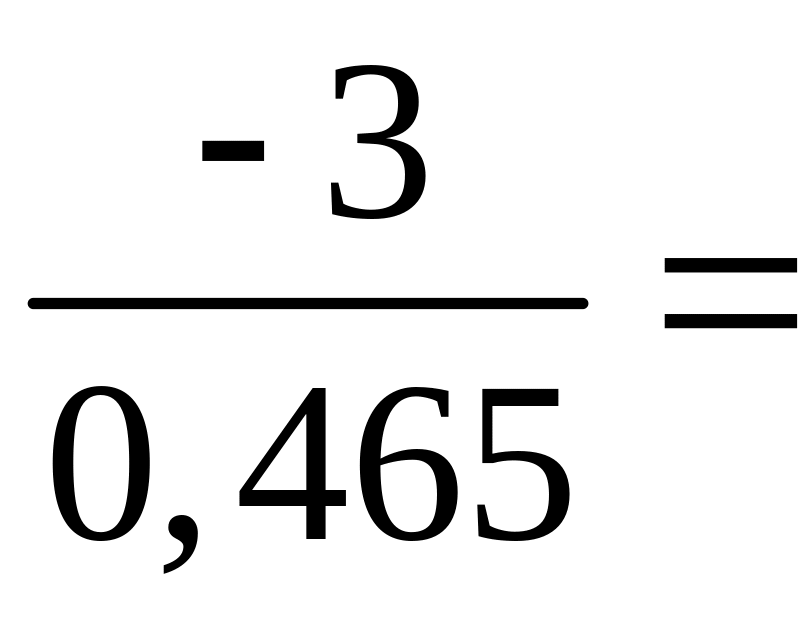
Критическая область для альтернативной гипотезы имеет вид

,

, .

Так как , то отклоняем гипотезу в пользу альтернативной .