Если же в качестве основного бинарного отношения берется , то отношение безразличия и отношение нестрогого предпочтения определяются на основекак

х~ у тогда и только тогда, когда неверно х у и неверно ух; х~ у тогда и только тогда, когда ху или неверно ху и неверно ух.

14. Теория полезности (проблема транзитивности, карты безразличия)

Отношение предпочтения наX транзитивно, если из того, что х предпочтительнее, чем у, а у предпочтительнее, чем z, сле­дует, что х предпочтительнее, чем z. В целом это свойство кажется разумным, поэтому будем предполагать, что оно выполняется в большинстве дальнейших рассуждений. Транзитивность нару­шается, если (х > у, у > z, х~ z) или (х у, уz, z х) для некоторых х, у и z из X.

Отношение безразличия (~) на X транзитивно, если из того, что х безразличен по отношению к у, а у безразличен к z, следует, что х безразличен по отношению к z. Отношение безразличия не транзитивно, если существуют х, у и z, для которых х ~ y, у ~ z и х z. Хотя во многих примерах нетранзитивных безраз­личий используется несколько критериев или характерных признаков, можно привести и простейшие «одномерные» примеры, демонстрирующие тот же факт. Для этого можно рассмотреть си­туацию с некоторым пороговым предпочтением, которое остается незамеченным благодаря несущественным или малым различиям в предпочтениях. В работе [38] это рассмотрено на примере чашки кофе, в которую добавляют один за другим маленькие кусочки сахара. Можно ожидать безразличного отношения к х и (х + 1) кусочкам сахара для х, скажем в пределах от 0 до 5000, но трудно ожидать одинакового отношения к двум чашкам кофе, в одной из которых нет сахара, а в другой х = 5000.

Поскольку отноше­ние ~ транзитивно, оно является отношением эквивалентности (транзитивным, симметричным, рефлексивным) и, следовательно, может быть использовано для разделения (разбиения) множества X на классы эквивалентности, или классы безразличия. Такие классы представляют собой непустые множества из X: если А и В — два различных класса и х лежит в А, & у в В, то х~ у тогда и только тогда, когда А =В\ если же х у,то х'у'для любого х' из А и каждого у' из В. На рис. 2 изображены классы безразличия для случая двух продуктов или двух характерных признаков.

11. Полезности и линейная функция полезности (линейная комбинация распределений)

Пусть и — вещественная функция, определенная на X. Функция и называется функцией полезности для отношения предпочтения наX, если и(х) > и(у) для любых x и y, таких, что х y; и называется совершенной функцией полезности для отношения на X, если для всехх и у из Х справедливо неравенство и(х) > и(у) тогда и только тогда, когда х у. Пусть отношение наХ может существовать, если только отношение является слабым упорядочением, и пусть для этого отношения определена совершенная функция полезностиu; тогда , если и толькои(х)=и(у). Отсюда следует, что классы безразличия в Х совпадают с подмножествами альтернатив, имеющих равную полезность.

Теория принятия решений использует различные процедуры, позволяющие формализовать предпочтение, т.е. выразить их в единой количественной мере. Основой для таких процедур является теория полезности, разработанная Дж. Фон Нейманом и О. Моргенштерном [33]. Ее математическая основа – система аксиом, в которых утверждается, что существует некоторая мера ценности, позволяющая упорядочить результаты решения. Эта мера называется функция полезности решений или полезностью.

Простым распределением вероятностей р называется вещественная функция Р, которая принимает положительные значения на большинстве элементов х из конечного множества X, а сумма всех значений р(х) равна единице. Мы не будем рассматривать непростые распределения. В зависимости от контекста распределения из Р часто называют ставками, играми, лотереями, альтернативами риска, смешанными стратегиями и рандомизированными стратегиями. Для любых распределений р и q из Р выражение называется прямой линейной комбинацией распределенийр и q; здесь  — действительное число, заключенное между 0 и 1. Таким образом, если 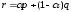, тодля любогоx из X. Если р и q принадлежат Р и , тотакже принадлежитР.

Предположим, что элементами Х являются некоторые суммы денег и пусть р(0 долл.)=0,3; р (10 долл.)=0,2; р (20 долл.)=0,5; q (7 долл.)=0,7; q (10 долл.)=0,3 и . Тогда ;r(0 долл.)=0,15; r(7долл.)=0,35; r(10 долл.)=0,25 и r(20 долл.)=0,25.

Линейная функция полезности

В соответствии с приведенными выше определениями вещественная функция и, заданная на множестве Р, является функцией полезности для отношения наР, если и(р)>и(q) для всех р q, и u— совершенная функция полезности для отношения наР, если для всех р и q из Р неравенство и(р)>и(q) справедливо тогда и только тогда, когда рq. В случае когда множество X содержит более одного элемента, множество Р будет неисчислимо, поэтому замечания из разд. 2.3 для неисчислимых множеств справедливы для функции и на множество Р.

В рассматриваемом случае наличие определенных структурных свойств у множества Р приводит к тому, что функция и обладает свойством линейности, которое определяется следующим образом:

(2.1)

для всех , лежащих между 0 и 1, и для всех р и q, принадлежащих Р. Функция полезности P, определенная для отношения наР, называется линейной функцией полезности, если для нее выполняется равенство (2.1).

11. Аксиомы линейной функции полезности

В данном разделе будут рассмотрены аксиомы (или условия) для отношения на множествеР, выполнение которых означает, что существует линейная функция полезности для отношения наР. В работе [21] предложены аксиомы (Al, А2, A3), которых достаточно для существования линейной функции полезности для отношения наР. Другой набор аксиом {Bl, В2, ВЗ} введен в работе [33]; выполнение этих аксиом является необходимым л достаточным условием существования совершенной линейной функции полезности для отношения на множествеР. В каждом случае X представляет собой любое непустое множество, причем не обязательно конечное или исчислимое. Аксиомы не означают, что полезность ограничена, хотя ограниченность полезности обыч­но возникает в результате применения аналогичных аксиом к не­простым распределениям вероятностей.

Первоначальная аксиоматика для совершенной функции полезности была предложена Нейма­ном и Моргенштерном в их известной книге [58], и поэтому совер­шенную линейную функцию и (или дополнительную к ней v на X) часто называют функцией полезности Неймана — Морген-штерна. Используется также выражение «полезность по Бернулли», поскольку Бернулли внес вклад в разработку этого вопроса [6].

При формулировке каждой аксиомы предполагается, что все р, q, r и s принадлежат множеству Р; в аксиомах А2 и В2 счита­ется, что а лежит строго между 0 и 1.

А1. Отношение на Р нерефлексивно.

А2. Если 0< а < 1 и р q и r s, то ар + (1 — а) r аq+ (1 — а) s.

A3. Если р q и rs, то ар -+ (1 — a) s аq + (1 — a) r для некоторого а, заключенного строго между 0 и 1.

B1. Отношение на Р является слабым упорядочением.

B2. Если 0 < а < 1 и р q, то ар +(1 — а)r аq + (1 — а) r

B3. Если р q и q r, то ар + (1 — а) r q и q (bр + (1 — b) r) для некоторых а и b, лежащих строго между 0 и 1.

Аксиомы А1 и В1 уже обсуждались выше (они означают, что отношение ациклично);А2 и В2 называют по-разному: аксио­мами независимости, аддитивности или условиями линейности. Линейные свойства функции и [см. уравнение (3)] получаются не­посредственно из этих аксиом. Рациональное обоснование аксиом А2 и В2 обычно дается следующим образом: сначала выбирают р и r с соответствующими вероятностями а и (1 — а), а затем со­ставляют выражение ар + (1 — а) r на основе ранее сделанного выбора.

11. Основы рационального поведения лица принимающего решения.

Одно из основных допущений экономической теории состо­ит в том, что человек делает рациональный выбор. Рациональ­ный выбор означает предположение, что решение человека яв­ляется результатом упорядоченного процесса мышления. Слово «упорядоченный» определяется экономистами в строгой мате­матической форме. Вводится ряд предположений о поведении человека, которые называются аксиомами рационального пове­дения.

При условии, что эти аксиомы справедливы, доказывается теорема о существовании некой функции, устанавливающей че­ловеческий выбор, — функции полезности. Полезностью назы­вают величину, которую в процессе выбора максимизирует личность с рациональным экономическим мышлением. Можно сказать, что полезность — это воображаемая мера психологиче­ской и потребительской ценности различных благ.

Человек, который следует аксиомам рационального выбора, называется в экономике рациональным человеком.

11. Нерациональное поведение (Эвристики, обьяснение отклонения от рационального поведения)

Приведем один из наиболее известных примеров нерационального поведения людей - «дилемму генерала» [6]. Генерал потерпел поражение в войне и хочет вывести свои войска (600 чел.) с территории противника. У него есть две возможные до­роги, и разведка дала оценки возможных потерь при выборе каждой из них. Данные о дорогах и возможных потерях пред­ставлены на рис.

Многочисленные эксперименты продемонстрировали откло­нение поведения людей от рационального, определили эвристи­ки, которые используются при принятии решений. Дадим пере­чень наиболее известных эвристик [7].

Суждение по представительности. Люди часто судят о ве­роятности того, что объект А принадлежит к классу В только по похожести А на типовой объект класса В. Они почти не учи­тывают априорные вероятности, влияющие на эту принадлеж­ность.

Суждение по встречаемости. Люди часто определяют веро­ятности событий по тому, как часто они сами сталкивались с этими событиями и насколько важными для них были эти встречи.

Суждение по точке отсчета. Если при определении веро­ятностей используется начальная информация как точка отсче­та, то она существенно влияет на результат.

Сверхдоверие. В экспериментах было показано, что люди чрезмерно доверяют своим суждениям, особенно в случаях, когда они выносят суждение о прошлых событиях.

Стремление к исключению риска. Многочисленные работы показывают, что как в экспериментах, так и в реальных ситуа­циях люди стремятся исключить ситуации, связанные с рис­ком. Они соглашаются на средние (и хуже средних альтерна­тивы, только чтобы не возникли ситуации, где хотя бы при очень малых вероятностях возможны большие потери.

Признание нерациональности человеческого поведения при­вело к поиску его причин. Среди этих причин называют [9]:

1. недостаток информации у ЛПР в процессе выбора;

2. недостаточный опыт ЛПР: он находится в процессе обу­чения и поэтому меняет свои предпочтения;

3) ЛПР стремится найти решение, оптимальное с точки зрения совокупности критериев (целей), строго упорядоченных по важности, но не может его найти;

4) различие между объективно требуемым временем для реализации планов и субъективным горизонтом планирования ЛПР.