26 Определение весовых коэффициентов (коэффициентов важности) критериев

В MAUT существенно используется понятие весов (коэффи­циентов важности) критериев. Считается, что ЛПР может найти коэффициенты — числа, которые определяют важность критери­ев. Отношения между весами критериев устанавливаются поис­ком точек безразличия на плоскостях двух критериев. В отличие от проверки условий независимости по предпочтению, по осям упорядочиваются значения критериев от худших к лучшим.

На рис. показана плоскость критериев С1, С2 .

Альтернати­вы А и К находятся в отношении безразличия, которое определя­ется так же, как и при проверке условия независимости по пред­почтению что по­зволяет записать U($200 млн, 40 мин.) = U($170млн, 90мин.)

В точке равновесия полезно­сти альтернатив равны.

Отметим, что U(40мин.)=1; U(90мин.)=0; U($100млн)=1; U($200млн)=0.

Для аддитивной функции полезности U =∑wiUi.

Тогда U($200 млн) w1 + U(40 мин.) w2 = U($170 млн) w1 + U(90 мин.) w2.

Отсюда w2(U(40 мин.)- U(90 мин.))= w1(U($170 млн)- U($200 млн)).

w2= w1 U($170млн).

Используя полученные ранее однокритериальные функции полезности определяем, что U($170млн)=0,4. Находим w2=0.4 w1 .Аналогичным образом определяется соотношение между весами критериев C1 и С3.

Пусть U($150млн)= 0,6, тогда w3=w1U($150млн)=0,6w1. Итак, мы выразили веса всех критериев через вес наиболее важного из них и упорядочили критерии по важности. Пусть w1=1, тогда w3=0,6w1=0,6; w2=0.4 w1=0,4.

Вопрос 28. Классические критерии тпр(0ценочные функции)

Чтобы прийти к однозначному и по возможности наивыгод­нейшему варианту решения даже в том случае, когда каким-то вариантам решений αi могут соответствовать различные усло­вия Qj, можно ввести подходящие оценочные (целевые) функ­ции. При этом матрица решений А=\\aij\\ сводится к одному столб­цу. Каждому варианту ri приписывается, таким образом, не­который результат aim характеризующий, в целом, все послед­ствия этого решения. Такой результат мы будем в дальнейшем обозначать тем же символом aim

Возникает, однако, проблема, ка­кой вложить смысл в результат aim

Если, например, последст­вия каждого из альтернативных решений характеризовать ком­бинацией из его наибольшего и наименьшего результатов, то можно принять

aim = min aij+ max aij .

Наилучший в этом смысле результат имеет вид

Кк = max aim = max (min aij+ max aij ). (1)

Формируя таким образом желаемый результат, кон­структор исходит из компромисса между оптимистическим и пессимистическим подходами.

Рассмотрим теперь некоторые другие оценочные функции, которые в данном примере мог бы выбрать конструктор, а так­же соответствующие им исходные позиции. Оптимистическая позиция:

Kо= max aim= max (max aij ). (2)

Из матрицы результатов решений (табл.) выбирается ва­риант (строка), содержащий в качестве возможного следствия наибольший из всех возможных результатов. Наш конструктор становится на точку зрения азартного игрока. Он делает ставку на то, что выпадет наивыгоднейший случай, и исходя из этого выбирает размеры изделия. Позиция нейтралитета:

Kн = max aim= max(3)

i j

Конструктор исходит из того, что все встречающиеся отклоне­ния результата решения от «среднего» случая допустимы, и вы­бирает размеры, оптимальные с этой точки зрения.

Пессимистическая позиция: - Критерий максимина (MM)

Kmm= max aim = max (min aij ). (4)

i i j

Конструктор исходит из того, что надо ориентироваться на наименее благоприятный случай и приписывает каждому из аль­тернативных вариантов наихудший из возможных результатов. После этого он выбирает самый выгодный вариант, т. е. ожида­ет наилучшего результата в наихудшем случае. Для каждого иного внешнего состояния результат может быть только рав­ным этому или лучшим.

Позиция относительного пессимизма: - Критерий Сэвиджа

Kc = min aim = min max(max aij _– aij). (5)

i i j j

Для каждого варианта решения конструктор оценивает потери в результате по сравнению с определенным по каждому вари­анту наилучшим результатом, а затем из совокупности наихуд­ших результатов выбирает наилучший согласно представлен­ной оценочной функции.

Пусть природа находится в состоянии Qs, найдем максимальный элемент s-го столбца табл. 1.1,

.

Мера сожаления определяется как разность

где еслиеслиТогда при состоя­нии природы Qs лучшей операцией является: для нее сожаление равно нулю. Изменяя последовательно значения s, s = 1,2,…, n, получим сожа­ление для каждой операции ai, i=1,2,…, m, при любом состояния природы Qs, s=1,2,…, n. Матрица сожалений представлена в табл. 1.2.

Для принятия решения к табл. 1.2 применяется критерий минимакса (minmax): для каждой операции ai, i=1,2,…, m, находится наибольшее со­жаление,

Таблица 1.2

Qj ai	Q1	Q2	…	Qn
a1	11	12	…	1n
a2	21	22	…	2n
…	…	…	…	…
am	m1	m2	…	mn

Затем среди членов последовательности , i=1,2,…, m, s = 1,2,…, n, находится минимальный

Последние два равенства соединим в одно:

(1.7)

Принимаемое решение – наилучшая операция

Критерий равновозможных состояний

По этому критерию выбирается та операция ai0, для которой сумма полезностей максимальна,

Kрс = . (6)

Принятие решений в условиях риска - Критерий Байеса-Лапласа (БЛ)

Ситуация ПР в условиях риска возникает в случаях, когда известны ап­риорные вероятности состояний природы

р(Q1), р(Q2), … , р(Qn),

.

Естественно воспользоваться этой дополнительной информацией. С этой целью для каждой операции аi находят взве­шенные суммы полезностей

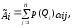i=1,2, …, m ,

и выбирают в качестве наилучшей ту операцию , для которой взвешен­ная сумма полезностей в (3.8) максимальна,

Кбл = (7)

Критерий Гурвица

Стараясь занять наиболее уравновешенную позицию, Гурвиц предложил критерий (HW), оценочная функция кото­рого находится где-то между точками зрения предельного оп­тимизма (2) и крайнего пессимизма (4):

Кг = max aim

i

max aim = max (cmin aij+ (1-c)max aij ), (8)

i i j j

где с — весовой множитель.

Правило выбора согласно HW-критерию формулируется на­ми следующим образом:

Матрица решений ||aij|| дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результа­тов для каждой строки Выбираются те варианты ai0, в строках которых стоят наибольшие элементы aij этого столбца.

Для с=1 HW-критерий превращается в ММ-критерий. Для с = 0 он превращается в критерий азартного игрока. Отсюда яс­но, какое значение имеет весовой множитель с. В технических приложениях правильно выбрать этот множитель бывает так же трудно,как правильно выбрать критерий. Вряд ли возмож­но найти количественную характеристику для тех долей опти­мизма и пессимизма, которые присутствуют при принятии реше­ния. Поэтому чаще всего весовой множитель с = 0,5 без возра­жений принимается в качестве некоторой «средней» точки зре­ния. При обосновании выбора применяют обратный порядок действий. Для приглянувшегося решения вычисляется весовой множитель с, и он интерпретируется как показатель соотноше­ния оптимизма и пессимизма.