Лекция 5

126

Лекция 5-2014

Рассматриваемые вопросы:

2.8. Переходные процессы в линейных электрических цепях постоянного тока (методы переменных состояния и операторный)

Анализ переходных процессов в электрических цепей постоянного тока методом переменных состояния.

Из всех известных методов расчета переходных процессов наиболее физичным является метод пространства состояний. Этот метод позволяет одновременно получать все интересующие нас величины токов и напряжений.

Переменные состояния представляют собой систему наименьшего числа внутренних независимых величин необходимых для полного определения поведения динамической системы. Переменные состояния – это токи индуктивностей и напряжения емкостей, именно они определяют состояние системы. В математической форме уравнения состояний для сложной цепи имеют вид:

x (t) – вектор состояния (размерность n);

A – матрица состояния (размерность n×n );

BU(t) – вектор-столбец (размерность n);

D(x,t) – расширенная матрица.

Сначала рассмотрим составление уравнения состояния на простейших цепях первого порядка (рис. 2.57). Вектором состояния является напряжение на конденсаторе после коммутации. Запишем второй закон Кирхгофа.

Рис. 2.57

.

Перепишем это уравнение относительно производной .

или

.

Такой вид уравнения называется нормальным. Таким образом, дифференциальное уравнение, разрешенное относительно производной называется нормальным.

Рассмотрим еще один пример. Определим ток через индуктивность (рис. 2.58).

Рис. 2.58

В данном случае вектором состояния является ток через индуктивность. Составляем уравнение по второму закону Кирхгофа.

.

Разрешаем это уравнение относительно производной и получаем уравнение в нормальной форме

,

или

.

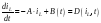Рассмотрим пример для цепи второго порядка. Вектором состояния являются переменные

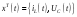
Записываем уравнения по второму закону Кирхгофа, в результате получаем систему дифференциальных уравнений:

Разрешим эту систему относительно производных, то есть запишем в нормальном виде

Выпишем матрицу состояния:

,

,.

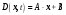Что бы проверить правильность составление матрицы состояния, нам нужно проверить ее собственные числа

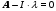
или

,

откуда

.

Если все сделано правильно, то это уравнение совпадает с уравнением входного сопротивления схемы

.

Отсюда

или

.

Проверим столбцовую матрицу

.

Результат должен дать вынужденные составляющие напряжения на конденсаторе и ток через катушку индуктивности.

Пример 2.14. Для электрической цепи, изображенной на рисунке, определить ток i_L (t) в катушке индуктивности и напряжения u_C1(t) и u_C2(t) на конденсаторах после включе- ния ЭДС, если Е = 100 В, R₁ = 20 Ом, R₂ = 100 Ом, С₁ = 20 мкФ, L =0,01 Гн.

Решение. Запишем уравнения, связывающие токи i_C1, i_C2 и напряжение u_L1 с напряжениями на конденсаторах и током индуктивности. Для этого используются первый и второй законы Кирхгофа. В нашем примере матрицы x(t), A и BU (t) будут равны

, , .

После подстановки числовых значений получаем:

, .

После определения матриц A и BF необходимо проверить правильность составления уравнения состояний. Это можно сделать, определив корни характеристического уравнения через входное сопротивление схемы:

Корни характеристического уравнения p₁, p₂, p₃ должны полностью совпасть с собственными числами λ₁, λ₂, λ₃ матрицы состояния А

.

Затем следует проверить вынужденные составляющие решений. В схеме после коммутации их легко найти, в нашем случае они определяются соотношениями:

.

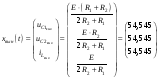С помощью матричных соотношений их легко проверить:

Таким образом, мы убедились, что система уравнений состояния составлена правильно.

■

Операторный метод анализа переходных процессов в электрических цепях постоянного тока.

Преобразование Лапласа и его свойства. Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраически-ми уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.

В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительной переменной t в область комплексной переменной р:

При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексной переменной на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.

Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением

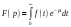, (2.18)

где  функция действительной переменной t, определенная при (при) и удовлетворяющая условиям ограниченного роста

где множитель М и показатель роста с₀  положительные действительные числа. На рис. 2.59 изображена область определения функции комплексной переменной F(p).

Рис. 2.59. Область определения функции комплексной переменной F(p)

Обратное  преобразование Лапласа определяют из  решения (2.18):

(2.19)

Функция F(p), определяемая уравнением (2.18), носит название изображения по Лапласу, а функция f(t) в (2.19) — оригинала. Следовательно, оригинал и изображение пред­ставляют собой пару функций действительной f(t) и комплексной F(p) переменных, связанных преобразованием Лапласа. Для сокращенной записи преобразований (2.18), (2.19) используют следующую символику:

, , ,

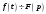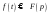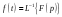
где L  оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия _{или символ}. .

Рассмотрим основные свойства преобразования Лапласа.

Свойство линейности является следствием линейности преобразования Лапласа, его можно записать в форме

_(2.20.)

где А, В  постоянные коэффициенты разложения. Свойство (2.20) легко доказать, если применить к левой части соотношения (2.20) прямое преобразование Лапласа ( 2.18).

Дифференцирование оригинала. При ненулевых начальных условиях: f(0_) ≠ 0 дифференцирование ориги-нала соответствует следующему условию:

_если

,

то

Применив эту теорему к производным высших порядков, получим

(2.20, а)

При нулевых начальных условиях выражение (7.6) упрощается

Интегрирование оригинала. Если

,

то

,

т.е. изображение интеграла кратности n функции f(t)

соответствует умножению изображения функции на при нулевых начальных условиях:

.

Доказательство осуществляется путем использования свойства дифференцирования оригинала (7.6), (7.7).

Изменение масштаба независимой переменной (теорема подобия)

, (2.21)

где а  постоянный вещественный коэффициент. Свойство (2.21) легко доказывается путем замены независимой переменной τ = at в прямом преобразовании Лапласа (7.2).

Смещение в области действительной переменной (теорема запаздывания):

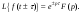(2.22)

Из соотношения (2.22) следует, что сдвиг оригинала по оси времени наτсоответствует умножению изображения на е^±pτ.

Смещение в области комплексной переменной (теорема смещения):

(2.23)

Теорема (2.23) следует непосредственно из прямого преобразования Лапласа, если в (2.18) вместо f(t) подставить e^±λtf(t). Причем X может быть как действительной, так и комплексной величиной.

Дифференцирование и интегрирование оригинала по параметру (свойство коммутативности):

, (2.24)

. (2.25)

Для доказательства свойств (2.24), (2.25) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (2.18) по параметру х.

Произведение изображений:

(7.14)

Интегралы в (7.14) носят название свертки функций и .

Дифференцирование изображения:

.(7.15)

Интегрирование изображения:

(7.16)

Предельные соотношения для оригинала и изображения:

В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(t) и единичной импульсной функции δ(t) (функция Дирака).

Единичная ступенчатая функция (функция Хэвисайда). Единичная функция (рис. 2.60, а) задается уравнением

Рис. 2.60.

. (2.26)

Изображение функции (2.26) будет равно:

, т.е. .

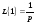Единичная импульсная функция (функция Дирака). Она задается выражением

.

Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при τ → 0) единичного импульса (см. рис. 2.61, б), площадь которого равна единице:

.

Найдем изображение единичной импульсной функции в форме изображения разности двух единичных функций величины 1(t), сдвинутых друг относительно друга на τ (рис. 2.61).

Рис. 2.61.

Для этих функций с учетом теоремы запаздывания имеем:

,

.

Для результирующего изображения с учетом свойства линейности получим

.

При изображение единичной импульсной функции

.

Экспоненциальный сигнал 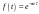при t > 0

,

т.е.

.

Подобным же образом можно найти изображение по Лапласу других функций, удовлетворяющих условию (7.3). В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций. В табл. 7.1 приведены оригиналы и их изображения наиболее часто встречающихся в теории электрических цепей функций.

Одним из интересных свойств функции δ(t) является ее фильтрующее свойство, определяемое равенством (рис. 2.62):

Рис. 2.62

Теорема разложения. Для нахождения оригинала по изображению можно воспользоваться либо таблицами, либо использовать обратное преобразование Лапласа (2.19). Однако вычисление оригинала с помощью (7.4) обычно оказывается весьма сложным. Поэтому, для упрощения расчетов применяют теорему разложения, которая позволяет при нахождении оригинала заменить операцию интегрирования в (2.19) операцией суммирования, что значительно упрощает вычисления. Наиболее строгий вывод этой теоремы можно осуществить на основании теоремы вычетов. Здесь мы ограничимся выводом формул разложения применительно к изображению, представляющему собой рациональную дробь:

, (*)

где a_n, a_n-1,…, a₁, a₀; b_m, b_m-1,…, b₁, b₀ вещественные коэффициенты, не имеющие общих корней.

Для нахождения оригинала разложим на простые дроби

(2.27)

где − простые корни характеристического уравнения

− коэффициенты разложения.

Оригиналы и изображения некоторых функций приведены в следующей таблице.

Таблица 2.1

Оригиналы и изображения некоторых функций

№ п/п	Оригинал f(t)	Изображение F(p)
1
2
3	1 -
4	sin ωt
5	sin (ωt + φ)
6
7	cos ωt
8	cos (ωt + φ)
9
10	A – const
11	At
12

,

Для нахождения умножим обе части последнего выражения на и перейдем к пределу

.

По правилу Лопиталя в левой части с учетом того, что правая часть (2.27)) равна , получаем

где

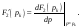
Подставим значение в (2.27)

.

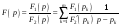Поскольку изображение (см. табл. 7.1), то

в соответствии со свойством линейности преобразования Лапласа окончательно получаем

. (2.28)

Последняя формула есть математическая формулировка теоремы разложения. Она позволяет найти оригинал по изображению в случае простых корней. Если же среди корней есть один нулевой , т.е. , то теорема разложения примет вид:

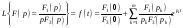. (2.29)

Формулу (2.29) можно получить, если подставить в (2.28) вместо F₂(p) значение pF₃(p) и осуществить операцию дифференцирования.

Если среди корней уравнения (2.27) (полюсов функции F(p)) имеются комплексно-сопряженные корни р_k и р_k+1, то в формуле (2.29) достаточно взять р_k, а для р_k+1 взять сопряженное значение, при этом сумма соответствующая двум этим корням с учетом дей­ствительности f(t) будет равна

При этом в уравнении для f(t) появятся составляющие типа

Ae^-αtsin(ω_ct +θ).

Теорему разложения можно обобщить и на более общие случаи. В частности, если среди полюсов (*) имеются полюса кратности l, то в оригинале f(t) появятся слагаемые типа (6.8).

Пример 2.15. Получить оригинал функции , изображение которой имеет вид

.

Решение. Очевидно, что

,

.

Получим в виде (*).

Корни характеристического уравнения

равны , , .

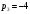Функция при p = p_k имеет значения , , .

Производная при тех же значениях корней имеет значения 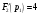, , . Теперь в соответствии с (7.30) окончательно получим

Учитывая, что среди корней характеристического уравнения F₂(p) = 0 имеем один нулевой корень, при нахождении f(t) можно было воспользоваться и формулой (7.31). Действительно, если обозначим

,

то

.

Значения корней уравнения

будут равны , . Выражение функции принимает значения , , , а выражение производной

принимает значения , , .

С учетом полученных значений окончательно получим

что полностью совпадает с предыдущим результатом.

Основные законы и элементы электрических цепей в операторной форме. Для получения операторных выражений законов электрических цепей необходимо получить операторные представления описаний этих законов в действительной форме.

Первый закон Кирхгофа: действительная формулировка – алгебраическая сумма токов ветвей сходящихся в узле в любой момент времени равна нулю

.

Преобразуем по Лапласу обе части этого равенства, учитывая свойство линейности (2.20). Тогда получим первый закон Кирхгофа в операторной форме

Его формулировка: алгебраическая сумма операторных токов ветвей, сходящихся в узле, равна нулю.

Второй закон Кирхгофа: действительная формулировка – алгебраическая сумма напряжений на ветвях замкнутого контура в любой момент времени равна нулю

На основании свойства линейности после преобразования по Лапласу этого равенства получим второй закон Кирхгофа в операторной форме

Его формулировка: алгебраическая сумма операторных напряжений на ветвях замкнутого контура равна нулю.

 Закон Ома: Введем в рассмотрение операторное сопротивление Z(p) участка цепи, которое определим как отношение операторного напряжения к операторному току участка цепи при нулевых начальных условиях:

где − операторная проводимость.