
- •ВВЕДЕНИЕ
- •МОДУЛЬ I: ОСНОВЫ МЕХАНИКИ
- •1. Механическое движение
- •1.1. Движение материальной точки
- •1.1.1. Скорость
- •1.1.2. Ускорение
- •1.1.3. Движение по окружности
- •1.1.4. Равномерное движение
- •1.1.6. Равноускоренное движение
- •1.2. Движение твердого тела
- •1.3. Динамика материальной точки
- •1.3.1. Первый закон Ньютона
- •1.3.2. Второй закон Ньютона
- •1.3.3. Третий закон Ньютона
- •1.4. Движение системы тел
- •1.4.1. Закон изменения и сохранения импульса системы тел
- •1.4.2. Центр инерции и центр масс системы тел
- •1.4.3. Уравнение движения центра масс
- •1.4.4. Движение тела переменной массы
- •1.5. Силовое поле
- •1.5.1. Центральное и однородное силовые поля
- •1.5.2. Энергия. Работа сил поля. Мощность
- •1.5.4. Кинетическая энергия
- •1.5.5. Потенциальная энергия
- •1.5.6. Закон измнения и сохранения механической энергии системы тел
- •1.5.7. Потенциальная кривая
- •1.5.8. Соударение тел
- •1.6. Неинерциальные системы отсчета
- •1.6.1. Силы инерции
- •1.6.2. Принцип эквивалентности
- •1.6.3. Сила тяжести и вес
- •1.7. Элементы теории относительности
- •1.7.1. Постулаты Эйнштейна
- •1.7.2. Преобразования Лоренца
- •1.7.3. Относительность одновременности событий
- •1.7.4. Относительность длин
- •1.7.5. Пространственно-временной интервал
- •1.7.6. Релятивистский закон сложения скоростей
- •1.7.7. Релятивистская масса
- •1.7.8. Основной закон релятивисткой механики
- •1.7.9. Связь массы, импульса и энергии в релятивистской механике
- •1.8. Динамика твердого тела
- •1.8.1. Момент силы
- •1.8.2. Момент пары сил
- •1.8.3. Момент импульса и момент инерции материальной точки
- •1.8.4. Момент инерции твердого тела
- •1.8.5. Свободные оси вращения. Главные оси инерции
- •1.8.6. Тензор инерции тела
- •1.8.7. Работа, совершаемая при вращательном движении
- •1.8.8. Кинетическая энергия вращающегося тела
- •1.8.9. Основной закон динамики вращательного движения
- •1.8.10. Уравнение моментов
- •1.8.12. Гироскопы
- •1.9. Элементы динамики сплошных сред
- •1.9.1. Неразрывность струи
- •1.9.2. Уравнение Бернулли
- •1.9.3. Движение тел в жидкостях и газах
- •МОДУЛЬ II: КОЛЕБАНИЯ И ВОЛНЫ
- •2. Механические колебания
- •2.1. Гармонические колебания
- •2.1.1. Характеристики и график гармонических колебаний
- •2.1.2. Метод векторных диаграмм (вращающихся амплитуд)
- •2.1.3. Сложение колебаний
- •2.1.4. Скорость и ускорение при гармонических колебаниях
- •2.1.5. Дифференциальное уравнение свободных гармонических колебаний
- •2.1.6. Маятники
- •2.1.7. Энергия гармонического осциллятора
- •2.1.8. Затухающие колебания
- •2.1.9. Вынужденные колебания. Резонанс
- •2.2. Волны
- •2.2.1. Уравнение плоской бегущей волны
- •2.2.2. Волновое уравнение
- •2.2.3. Энергия волны
- •2.2.4. Интерференция волн
- •2.2.5. Эффект Доплера

101
МОДУЛЬ II: КОЛЕБАНИЯ И ВОЛНЫ
2. Механические колебания
Колебаниями называются процессы (движения или изменения состояния), повторяющиеся во времени. Колебательные процессы могут иметь различную природу. Различают механические, электромагнитные, тепловые и другие колебания.
Система, совершающая колебания, называется колебательной системой. Свободными (собственными) называют колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему.
Колебания называют периодическими, если значения всех физических величин, характеризующих колебательную систему и изменяющихся при еѐ колебаниях, повторяются через равные промежутки времени. Этот повторяющийся процесс называют полным колебанием. Время одного полного колебания называется периодом колебания
T Nt ,
N число полных колебаний, совершенных за время t. Частотой колебаний называется величина
Nt ,
равная числу полных колебаний, совершающихся за единицу времени. Видно, что
T 1 , T1 ,
т. е. период и частота колебаний выражаются взаимно обратными числами. Циклической или круговой частотой периодических колебаний называ-
ется величина
2 2T .
2.1.Гармонические колебания
2.1.1.Характеристики и график гармонических колебаний
Периодические колебания называют гармоническими, если они подчиняются закону косинуса или синуса. Допустим, материальная точка соверша-

102
ет гармонические колебания вдоль оси x около положения равновесия, принятого за начало координатной оси. Зависимость координаты x от времени t имеет вид:
x
A
0
T
x
2
Рис. 2.1.
x Acos( t ) или x Asin( t ) ,
где A амплитуда колебаний. Амплитудой колебаний называют максимальное значение колеблющейся величины.
t Значение колеблющейся величины в произвольный момент времени t определяется значением фазы колебаний величины, стоящей под знаком
косинуса или синуса
t .
Величина представляет собой начальную фазу колебаний.
График гармонического колебания в зависимости от времени t и от фазы φ показан на рис 2.1.
2.1.2. Метод векторных диаграмм (вращающихся амплитуд)
Гармонические колебания можно представить в виде проекции на горизонтальную ось x или вертикальную ось y вращающегося вектора A , модуль которого равен амплитуде A рассматриваемых колебаний (рис. 2.2). В начальный момент времени угол, который вектор A составляет с осью x, ра-
|
|
|
|
|
|
y |
|
|
A |
|
|
|
|
t |
A |
||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
t 0 |
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
|
x |
|
x Acos( t ) |
||||
|
|
|
|
|
|
|
|
|
Рис. 2.2.
вен начальной фазе колебаний α. Вращение вектора A происходит по закону изменения фазы колебаний t с угловой скоростью равной цикличе-

103
ской частоте колебаний . Проекция вектора на горизонтальную ось x изменяется по закону косинуса x Acos( t ) , а на вертикальную ось y по закону синуса y Asin( t ) .
2.1.3. Сложение колебаний
Если колебательная система одновременно участвует в нескольких колебательных процессах, то возникает результирующее движение или колебание, называемое суммой этих колебаний. Различают два предельных случая – сложение колебаний одного направления и сложение взаимно перпендикулярных колебаний.
2.1.3.1. Сложение колебаний одного направления. Биения
Рассмотрим результирующее колебание шара 1, который колеблется относительно шара 2 на пружине а и вместе с ша-
бром 2 колеблется на пружине б в одном и том же направлении
2 |
|
вдоль вертикальной оси (рис. 2.3). Допустим, что колебания |
||
|
|
|
|
|
|
а |
происходят с одинаковой частотой по законам: |
||
|
|
|
|
|
1 |
|
|
x1 A1 cos( t 1), |
|
х |
|
|
x2 A2 cos( t 2 ), |
|
Рис. 2.3. |
где A1 |
– амплитуда первого колебания, 1 |
– начальная фаза пер- |
|
|
|
|||
вого колебания, A2 |
– амплитуда второго колебания, 2 |
– начальная фаза вто- |
||
рого колебания. |
|
|
||
|
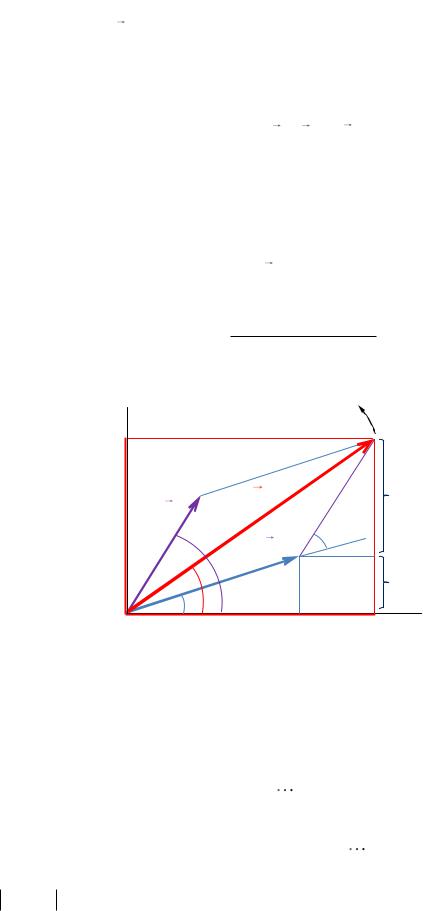
Сложим эти колебания, воспользовавшись методом векторных диа- |
|||
грамм. Проведем векторы A1 и A2 под углами 1 и 2 |
к горизонтальной оси |
|||
(рис. 2.4). Так как эти векторы вращаются с одинаковой угловой скоростью , то их взаимное расположение не изменяется. Значит, не изменяется и угол между векторами, соответственно разность фаз колебаний 2 1 остается постоянной. Результирующее колебание x x1 x2 можно представить как
сумму проекций векторов A1 и A2 на ось х или как проекцию результирую-
щего вектора A A1 A2 . То есть
x Acos( t ) ,
|
|
|
|
|
104 |
|
|
|
|
|
|
||
где A – |
амплитуда результирующего колебания, равная модулю результи- |
||||||||||||
рующего вектора A , |
– начальная фаза результирующего колебания равная |
||||||||||||
углу, под которым расположен этот вектор к горизонтальной оси x в началь- |
|||||||||||||
ный момент времени. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Результирующую амплитуду находим по теореме косинусов из тре- |
|||||||||||||
угольника, образованного векторами A1 , |
A2 |
и A (рис. 2.4): |
|
||||||||||
|
|
A2 A2 |
A2 |
2A A cos( |
2 |
) . |
|
(2.1) |
|||||
|
|
|
1 |
2 |
1 |
2 |
|
|
1 |
|
|
||
Начальную фазу результирующего колебания можно выразить через |
|||||||||||||
тангенс угла, образуемого вектором A с осью x : |
|
|
|
|
|
||||||||
|
|
tg A1 sin 1 |
A2 sin 2 . |
|
|
|
|||||||
|
|
|
|
A cos |
A cos |
2 |
|
|
|
||||
|
|
|
|
1 |
1 |
|
|
2 |
|
|
|
|
|
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
A2 sin 2 |
|
||
|
A2 |
|
|
|
|
|
|
|
|
|
|||
|
sin |
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 sin 1 |
|
||
|
|
|
|
A1 cos 1 |
|
A2 cos 2 |
|
||||||
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
Acos |
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. 2.4. |
|
|
|
|
|
|
|||
Проанализируем выражение (2.1) в зависимости от разности фаз скла- |
|||||||||||||
дываемых колебаний 2 1 : |
|
|
|
|
|
|
|
|
|
|
|
||
Если 2 1 2m (где m 0,1, 2, |
), то cos( 2 |
1) 1, и амплитуда ре- |
|||||||||||
зультирующего колебания принимает максимальное значение A A1 A2 . |
|
||||||||||||
Если |
2 1 (2m 1) |
|
(где m 0,1, 2, |
|
), |
то |
cos( 2 1) 1, |
и |
|||||
амплитуда результирующего колебания принимает минимальное значение |
|||||||||||||
A A1 A2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|

105
A3 |
|
|
|
Если необходимо сложить не два, а несколько |
|
|
|
|
колебаний, то в этом случае пользуются графиче- |
||
|
3 |
|
|||
|
|
ским построением, выполненным |
по масштабу |
||
|
|
|
|
||
A |
A2 |
|
|
(рис. 2.5). Измеряя модуль результирующего векто- |
|
|
|
2 |
|
ра A в масштабных единицах, определяют ампли- |
|
A1 |
|
|
|||
1 |
|
|
x |
туду результирующего колебания, а измеряя угол |
|
|
|
|
|
||
|
|
|
|
, находят начальную фазу этого колебания. |
|
Рис. 2.5. |
|
|
Рассмотрим случай, когда два складываемых |
||
|
|
|
|
||
|
|
|
|
колебания одного направления мало отличаются по |
|
частоте: пусть 1 |
больше, чем 2 на величину . В процессе вращения |
||||
вектор A1 |
постепенно догоняет вектор A2 и, когда вектор A1 |
станет направ- |
|||
ленным в ту же сторону, что и вектор A2 , результирующее колебание достигнет максимальной амплитуды A A1 A2 . При этом разность фаз 2 1 0 .
Далее разность фаз начнет увеличиваться, и, когда вектор A1 станет направ-
лен противоположно вектору A2 , результирующее колебание достигнет минимальной амплитуды A A1 A2 . При этом разность фаз 2 1 . В ре-
зультате получаются колебания с периодически изменяющейся амплитудой.
Периодические изменения амплитуды колебаний, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний одинаковы и равны A , а их частоты равны соответственно и . Начало отсчета вре-
мени выберем так, чтобы начальные фазы колебаний были равны нулю. Запишем уравнения этих колебаний и сложим их:
x1 Acos( )tx2 Acos t
x A cos( )t cos t .
Применяя формулу для суммы косинусов
cos cos 2cos cos , 2 2
получим x 2Acos 2 t cos( 2 )t , а, с учетом того, что ,
106
x 2Acos 2 t cos t .
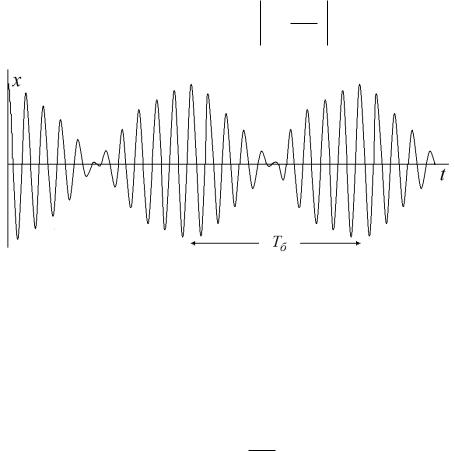
Задавая значения , и амплитуды A , построим график зависимости x от времени t (рис. 2.6). Результирующее колебание можно рассматривать как гармоническое колебание с частотой , амплитуда которого Аб медленно изменяется по закону
Aб 2A cos 2 t ,
Рис. 2.6.
т. е. возникают колебания, модулированные по амплитуде. Период изменения амплитуды результирующего колебания называется периодом биений Tб , он
равен
Tб 2 .
2.1.3.2. Сложение взаимно перпендикулярных колебаний
Рассмотрим маятник, который может совершать колебания одновременно в двух взаимно перпендикулярных направлениях. Для характеристики его положения нужно задать две величины, например, координаты x и y :
x Acos t , |
(2.2) |
y Bcos( t ) . |
(2.3) |
Такими уравнениями описывается движение тела, закрепленного на двух парах одинаковых пружин или движение математического маятника
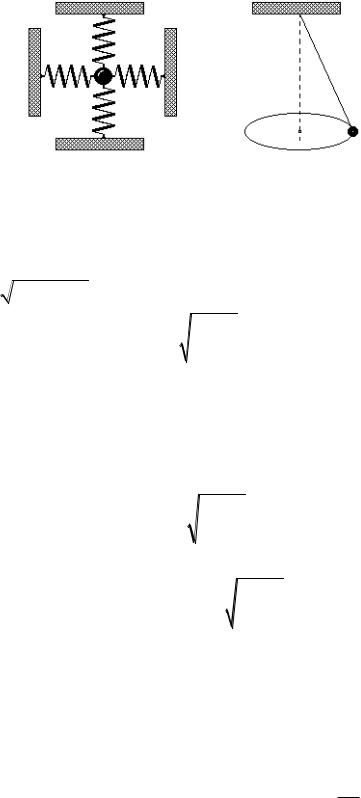
107
(рис. 2.7). Движение таких маятников представляет собой сумму колебаний в направлениях x и y. Чтобы получить уравнение траектории маятника, нужно исключить из уравнений (2.2) и (2.3) параметр t . Из (2.2) следует, что
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.7. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos t |
x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.4) |
||||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а так как sin t 1 cos2 t , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin t |
1 |
|
x |
. |
|
|
|
|
|
|
|
|
|
|
(2.5) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|||||||||
Применим тригонометрическую формулу косинуса суммы для уравне- |
||||||||||||||||||||||||||||||||||||||||||
ния (2.3): cos t cos sin sin t |
y |
. Учитывая (2.4) и (2.5), получим: |
||||||||||||||||||||||||||||||||||||||||
B |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
cos sin |
|
|
1 |
|
x |
|
|
|
y |
. |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
B |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
cos |
y |
sin |
1 |
|
x2 |
|
|
|
|
|
|||||||||||||||||||||||||||||
Сделав переносы |
|
|
|
|
|
|
|
|
|
|
|
|
и возведя обе части |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
A2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
A |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
уравнения в квадрат, придем к следующему выражению |
|
|||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
|
x |
cos2 2 |
x |
|
y |
cos |
y |
|
sin2 |
|
x |
|
sin2 |
. |
||||||||||||||||||||||||||||
|
2 |
|
|
2 |
|
2 |
||||||||||||||||||||||||||||||||||||
|
A |
|
|
|
|
A B |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
||||||||||||||
x2
После преобразований переноса и выноса за скобки дроби A2 , запишем
108
x |
2 |
sin2 cos2 2 |
x |
|
y |
|
y |
2 |
|
|
|
|
cos |
|
sin2 |
. |
|||||
|
2 |
A |
B |
B |
2 |
|||||
A |
|
|
|
|
|
|
||||
Учитывая, что sin2 cos2 1, получим
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
2 |
x |
|
y |
cos sin2 |
. |
|
|
|
|
|
(2.6) |
|||
|
2 |
2 |
A |
|
|
|
|
|
|
|||||||||
|
A |
B |
|
|
B |
|
|
|
|
|
|
|
|
|
|
|||
Из аналитической геометрии известно, что это уравнение эллипса. Зна- |
||||||||||||||||||
чит, тело будет двигаться по эллиптической траектории. |
|
|
|
|
|
|
|
|||||||||||
Рассмотрим частные случаи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) Разность фаз складываемых |
колебаний |
равна |
нулю, |
тогда |
||||||||||||||
sin 0, cos 1, и уравнение (2.6) принимает вид |
x |
|
y 2 |
0 или |
y |
B |
x |
|||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
A |
|
B |
|
|
A |
|
|||
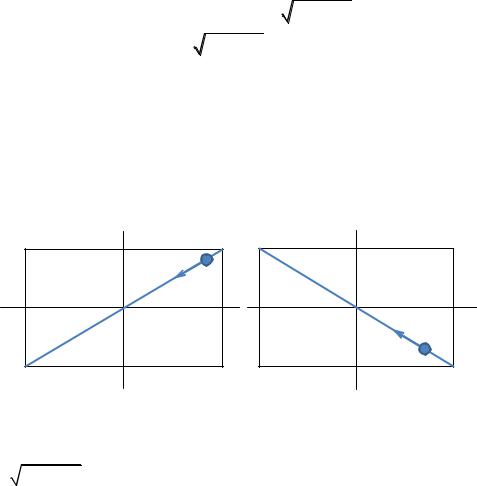
. Получилось уравнение прямой линии. Тело, перемещаясь по этой прямой (рис. 2.8 а), совершает результирующее гармоническое колебание в первом и
|
|
|
|
|
|
|
|
|
|
|
|
третьем координатных углах по закону r |
|
A2 B2 cost , где r расстоя- |
|||||||||
|
|
|
|
|
|||||||
ние от тела до начала координат, |
A2 B2 амплитуда этого колебания. |
||||||||||
2) |
Разность фаз складываемых колебаний , тогда sin 0, cos 1 |
||||||||||
, и уравнение (2.6) принимает вид |
|
x |
|
y 2 |
0 . Получилось уравнение пря- |
||||||
|
|
|
|
||||||||
|
|
||||||||||
|
|
|
|
|
A |
|
B |
|
|
|
|
мой |
y |
B |
x . Тело, перемещаясь по этой прямой, совершает результирую- |
||||||||
|
|||||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
y |
|
y |
|
B |
r |
B |
|
|
|
|
|
|
A x |
r |
A x |
|
|
|
|
a |
|
б |
|
|
|
|
Рис. 2.8.
щее гармоническое колебание во втором и четвертом координатных углах по закону r 
 A2 B2 cost (рис. 2.8 б).
A2 B2 cost (рис. 2.8 б).
