95

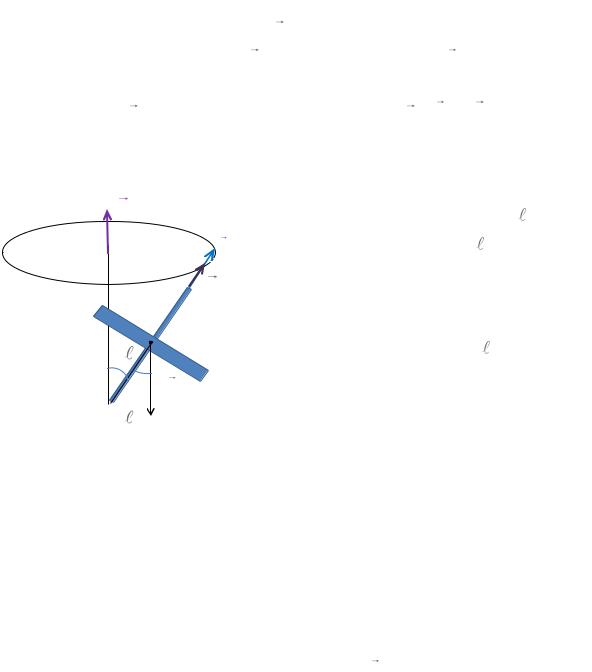
вертикалью. На рис. 1.68 вектор M направлен за плоскость чертежа. В ту же сторону направлен и вектор dL . В результате вектор L , а, следовательно, и ось гироскопа будут прецессировать, т. е. вращаться вокруг вертикали с угловой скоростью , направленной вверх. Векторы , L и M образуют правовинтовую систему.

C

называемый свободный симметричный волчок. Это можно осуществить с помощью карданова подвеса. Карданов подвес состоит из двух колец, внешнее из которых свободно поворачивается вокруг вертикальной оси (оси z ), а внутреннее – вокруг горизонтальной оси (оси х). Ось гироскопа направлена вдоль оси y и опирается на внутреннее кольцо, что обеспечивает ей возможность свободно поворачиваться в пространстве в любых направлениях. В силу отсутствия момента внешних сил выполняется закон сохранения момента импульса вращающегося гироскопа. Вектор L , а, следовательно, и ось вращения гироскопа сохраняют своѐ направление в пространстве, как бы ни перемещался карданов подвес. На этом принципе устроен гироскопический компас.

1.9. Элементы динамики сплошных сред

1.9.1. Неразрывность струи

Помимо движения твердых тел механика рассматривает также движение сплошных сред – жидкостей и газов. Течение жидкости представляет собой сложное явление. Для упрощения его описания вводят модельное пред-

96

ставление об идеальной жидкости. В такой жидкости слои, перемещаясь друг относительно друга, не испытывают трения.

Проведем в движущейся жидкости линии так, чтобы касательная к ним в каждой точке совпадала с вектором скорости v . Эти линии называют линиями тока. Часть жидкости, ограниченная линиями тока, называется трубкой тока. Если вектор скорости в каждой точке остается постоянным, то течение жидкости называют стационарным. Поток жидкости может быть близок к стационарному только при малой скорости движения.

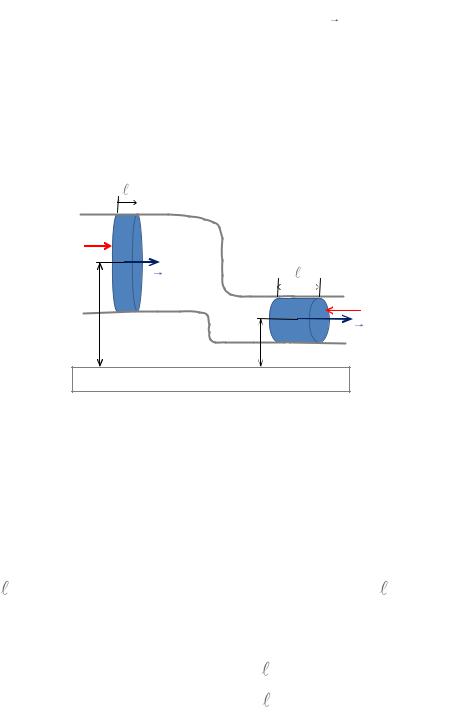
Рассмотрим трубку тока с переменным поперечным сечением S (рис.

1

p1 S1

Рис. 1.69

1.69). Эту трубку можно представить себе как обычную трубу переменного сечения, только при движении по такой трубе жидкость не должна взаимодействовать с ее стенками. Пусть сечения трубы S1 и S2 находятся на разных высотах h1 и h2. Будем считать скорость жидкости постоянной в пределах одного сечения. За время t жидкость в трубе сечением S1 переместится на расстояние 1 v1t , а в трубе сечением S2 на расстояние 2 v2t , v1 и v2 скорости движения жидкости в трубах. Объемы жидкости, прошедшей через сечения S1 и S2 соответственно равны:

V1 S1 1 S1v1t; V2 S2 2 S2v1t.

Если жидкость несжимаема, то V1 V2 V и S1v1 S2v2 .

Следовательно, для несжимаемой жидкости величина произведения Sv в любом сечении одной и той же трубки тока одинакова. Это заключение представляет собой теорему о неразрывности струи.

Чем больше сечение трубки тока, тем меньше скорость движения жидкости и наоборот.

97

Так как скорость движения жидкости не изменяется со временем, то изменения, произошедшие в объеме, заключенном между сечениями S1 и S2 за время t, сводятся к перемещению массы m = V ( - плотность жидкости) от первого сечения ко второму. При этом энергия жидкости, заключенной между сечениями S1 и S2, остается постоянной. С течением времени в этом объеме происходит лишь замещение одних слоев жидкости на другие слои с равной энергией. В то же самое время масса жидкости m входит в сечение S1, имея энергию W1, и одновременно такая же масса m выходит из сечения S2, имея энергию W2. Следовательно, при течении жидкости по трубе происходит изменение ее энергии. Для жидкости массой m это изменение энергии равно W2

W1.

1.9.2. Уравнение Бернулли

При переходе жидкости с участка с большим сечением на участок с меньшим сечением скорость движения возрастает, следовательно, жидкость движется с ускорением. В горизонтальной трубе это ускорение возникает благодаря разности сил давлений F1 = p1S1 и F2 = p2S2, действующих на жидкость в сечениях S1 и S2. Если участки трубы расположены на разной высоте, то ускорение создается совместным действием сил тяжести и давления. При перемещении массы жидкости m от сечения S1 к сечению S2 эти две силы совершают над жидкостью работу.

Работа сил давления Ад над массой m при ее перемещении от сечения S1 к сечению S2 находится как:

Ад p1S1 1 p2S2 2 p1V1 p2V2 ;

Ад p1 p2 V .

Работа сил тяжести Ат над массой жидкости m при этом равна:

Aт mg(h1 h2 ).

Полная работа результирующей силы найдется как сумма этих работ:

A Aд Aт ( p1 p2 )V mg(h1 h2 ).

С учетом того, что m V ,

98

Полученная работа идет на приращение кинетической энергии рассматриваемой массы жидкости:

Приравнивая совершенную работу к изменению кинетической энергии, получим

Собирая слагаемые с индексом 2 слева, а с индексом 1 справа, придем к выражению:

Отсюда следует, что

p v2 gh const. 2

Последнее соотношение было получено в 1738 году швейцарским физиком Бернулли и носит его имя. Оно выражает закон сохранения энергии для стационарно текущей идеальной жидкости. Величину p называют статическим давлением (это давление показывал бы манометр, движущийся вместе с

p v2 = const. 2