данного состояния в состояние, в котором потенциальная энергия взаимодействия условно принимается равной нулю. Например, в состояние, когда тела будут бесконечно удалены друг от друга.

1.5.6. Закон измнения и сохранения механической энергии системы тел

где Fi – сила, действующая со стороны внешнего потенциального поля, fi –

равнодействующая внутренних консервативных сил, fi – диссипативная сила.

Умножим скалярно левую и правую части этого равенства на перемещение i-й частицы dri . Учитывая, что dri vidt , получим:

Fi dri fi dri fi* dri mivi dvi .

Правая часть равенства представляет собой дифференциал кинетической энергии:

Просуммируем такие равенства по всем частицам системы:

52

1.5.7. Потенциальная кривая

График зависимости потенциальной энергии тела от координат называют потенциальной кривой. Например, потенциальная кривая гравитационного взаимодействия изображена на рис. 1.27. Пусть диссипативных сил нет,

а потенциальная энергия тела зависит только от координаты х каким-либо произвольным образом (рис. 1.33). Проанализируем эту кривую. Полная механическая энергия тела W представляет собой сумму потенциальной и кинетической энергий. Чем меньше потенциальная энергия тела, тем больше кинетическая. В областях х < x1 и х3 < x < x5, согласно рисунку, потенциальная энергия тела больше полной энергии. Такая ситуация невозможна, и эти области в классической физике недоступны для движения тела. Область между точками х3 и x5 называют потенциальным барьером. Пройти над барьером тело может, только имея полную энергию, большую высоты барьера W > Wп. На рис. 1.33 при заданной полной энергии W тело имеет две области, доступные для движения: от x1 до х3 и от х5 до бесконечности. Область x1 х3 называют потенциальной ямой. Кинетическая энергия, а, значит, и скорость, тела на краях ямы в точках x1 и х3 равна нулю. Максимальную скорость тело имеет в точке х2, соответствующей дну потенциальной ямы.

Определим теперь направление силы потенциального поля, действующей на тело в разных областях пространства. Воспользуемся формулой связи силы и потенциальной энергии F gradWп. В нашем одномерном случае

Fx dWdxп .

54

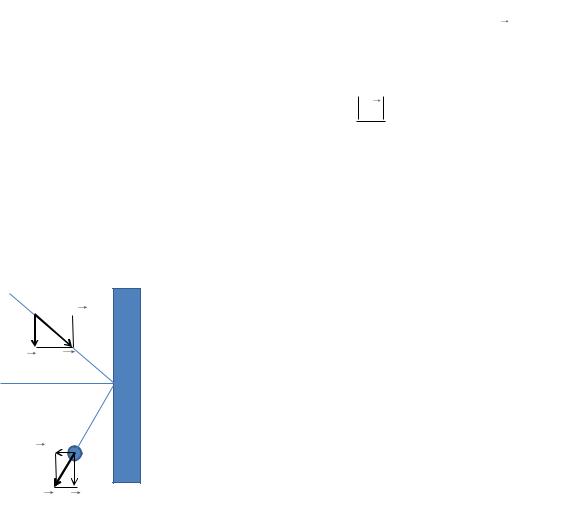
ления скорости ε. Пусть тело налетает на неподвижную преграду (рис. 1.34). Тогда коэффициент восстановления скорости равен отношению нормальных к преграде компонент скорости тела после и до удара:

В обоих равенствах соберем слагаемые с индексом 1 слева, а с индексом 2 справа:

55

или, расписав разность квадратов двух переменных,

Перепишем верхнее равенство. Также запишем результат деления нижнего равенства на верхнее. Получим

Выразив скорости первого и второго шаров после удара, найдем, что

где vC вектор скорости центра масс системы шаров. Из полученных соотношений видно следующее:

правлении. При m1<m2 он отскочит в противоположном направлении. Если

массы шаров равны, то второй шар приобретает скорость первого (v v ), а

2 1

первый останавливается (v 0 ) – происходит обмен скоростями;

1

если масса второго тела очень велика (массой m1 можно пренебречь по

сравнению с m2), и при этом v 0 то v v , то есть налетающий шар ―от-

2 1 1

ражается‖ от преграды, а его скорость не меняется по величине.

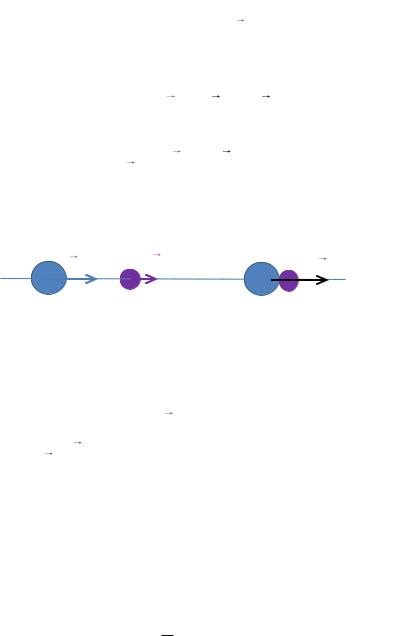
Теперь рассмотрим случай абсолютно неупругого удара (рис. 1.36).

56

В этом случае для расчета скорости тел v после удара можно применить только закон сохранения импульса, согласно которому

m1 m2 v m1v1 m2v2

и

Из полученного соотношения можно заключить, что при равенстве масс

тел

если второе тело до удара покоится (v2 0 ), то скорость первого тела после удара делится пополам: v v21 ;

при встречном движении с одинаковыми по величине скоростями после удара тела остановятся.

Найдем теперь, какое количество кинетической энергии переходит в тепловую форму при неупругом ударе:

Wк Wк,до Wк,после 12 (m1v12 m2v22 m1 m2 v2 )

Подставив значение общей скорости шаров после удара, раскрыв скобки и приведя подобные, получим:

Отсюда видно, что возможны два случая, когда вся кинетическая энергия тел переходит в тепловую форму:

тела равной массы движутся навстречу друг другу с одинаковыми скоростями;