Модуль I основы механики

1. Движение материальной точки

1. Механическое движение

Механика – это раздел физики, изучающий простейший вид движения материи – механическое движение. Механическим движением называют перемещение тел или частей тела относительно друг друга. При описании механических движений каких-либо тел надо указывать, по отношению к каким телам рассматривается это движение, т.е. какое тело мы условно считаем неподвижным. Это тело называют телом отсчета. Для описания движения необходима система отсчёта, включающая тело отсчёта, систему координат и систему отсчета времени (часы).

Материальной точкой в физике называют тело, размеры, форма и внутренняя структура которого в данной задаче несущественны. Положение материальной точки определяется радиус-вектором ,проведённым из начала координат к данной материальной точке.

Линию, вдоль которой движется материальная точка, называют траекторией движения. При движении материальной точки её радиус-вектор меняется в общем случае, как по модулю, так и по направлению. На рисунке 1.1 – радиус-вектор материальной точки в начальный момент отсчета времени.

Вектор перемещенияпредставляет собой приращение радиус-вектора, , и соединяет начальное и конечное положения материальной точки. 

Длину участка траектории Δs называют пройденным путем. Единицей измерения пути в международной системе единиц СИ является 1 метр (м).

Модуль перемещения всегда меньше или равен пути  ∆s. Знак равенства соответствует только случаю прямолинейного движения в одном направлении. Также равенство выполняется при условии, что рассматриваемый участок траектории бесконечно мал (=ds). При движении по замкнутой траектории перемещение равно нулю, чего нельзя сказать о пути.

Рис. 1.1.

2. Скорость

Отношение перемещения к промежутку времени, за который оно произошло, называют средним вектором скорости:

.

В тех задачах, где направление скорости не имеет значения, пользуются скалярной величиной – средним модулем скорости на данном участке

.

Иначе эту скорость называют средней путевой.

Определим вектор скорости в данный момент времени как предел отношения приt → 0. Эту скорость называют мгновенной скоростью. Мгновенная скорость равна производной радиус-вектора по времени и характеризует быстроту его изменения.

.

Вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки. Модуль мгновенной скорости:

.

Учитывая, что для бесконечно малого участка траектории , получим для модуля мгновенной скорости

Интегрируя выражение отt₁ до t₂, найдем длину пути, пройденного точкой за промежуток времени Δt = t₂ – t₁:

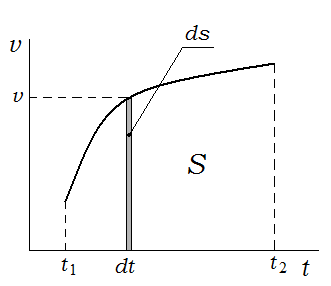
Если зависимость модуля скорости от времени задать графически (рис. 1.2), то площадь заштрихованной полоски, соответствующей бесконечно малому промежутку времени , будет равна элементарному пути:. Вся площадь под кривойv(t) равна пути 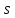за рассматриваемый промежуток времениΔt.

3. Ускорение

Быстроту изменения вектора скорости характеризует физическая величина, называемая ускорением. Среднее ускорение равно отношению изменения вектора скоростик промежутку времениΔt, за который оно произошло.

.

Мгновенным ускорением называют физическую величину равную производной вектора скорости по времени:

Учитывая, что , получим

Определим направление и величину мгновенного ускорения материальной точки. Пусть точка движется по криволинейной траектории (рис. 1.3). Вектор скорости в любой точке траектории представим в виде:, гдеv – модуль скорости, а – единичный вектор, направленный по касательной к траектории в направлении движения.

По определению . Взяв производную произведения, получим

Рис. 1.3.

.

Умножим числитель и знаменатель второго слагаемого на элементарный путь ds:

.

Учитывая, что , запишем:

.

Если промежуток времени dt бесконечно мал, то все соответствующие ему точки траектории находятся на дуге окружности радиуса R, сопряженной с траекторией на данном участке. Величину R называют радиусом кривизны, а центр этой окружности – центром кривизны траектории.

Найдём разность двух единичных касательных векторов , расположенных бесконечно близко на траектории. Уголмежду ними также бесконечно мал. При этом угол между векторамиистремится к 90°. Из подобия треугольника ОАВ и треугольника, образованного векторамии(на рисунке 1.3 он покрыт точками), определим, а вектор, где– единичный вектор, перпендикулярный вектору скорости и направленный к центру окружности (центру кривизны траектории). В итоге видим, что полное ускорение выражается формулой

и состоит из двух взаимно перпендикулярных векторов: тангенциального ускорения

и нормального ускорения

.

Полное ускорение является суммой этих векторов (рис. 1.4).

Рис. 1.4.

Тангенциальная компонента ускорения направлена вдоль траектории движения в направлении скорости , если(скорость увеличивается, рис. 1.5,а) и против скорости , если(скорость уменьшается, рис. 1.5,б). Проекция вектора тангенциального ускорения на направление скорости в первом случае положительна, а во втором отрицательна:.

Рис. 1.5.

Нормальная компонента ускорения направлена перпендикулярно касательной к траектории движения в направлении центра кривизны.

.

Применяя теорему Пифагора, получим модуль полного ускорения

.

Тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю. Если v = const., то и= 0.

Нормальная составляющая ускорения характеризует быстроту изменения вектора скорости по направлению. В случае прямолинейной траектории радиус кривизны стремится к бесконечности (R∞), значит и.

Если материальная точка движется, то ее радиус-вектор является функцией времени. Зависимость радиус-вектора движущейся материальной точки от времениназываюткинематическим уравнением движения. Выберем прямоугольную декартову систему координат и запишем радиус-вектор в проекциях на оси:

,

где – координаты материальной точки, равные проекциям радиус-вектора на оси координат: , а – единичные векторы в направлении координатных осейx, y и z (орты осей). В процессе движения координаты точки меняются, т. е. являются функциями времени. Зная зависимость координат от времени, можно найти положение точки в каждый момент времени, её скорость и ускорение. Действительно, взяв производную радиус-вектора по времени, найдём вектор скорости

,

,

где – проекции вектора скорости на оси координат. Применяя теорему Пифагора, определим модуль вектора скорости

.

Аналогичным образом определим вектор мгновенного ускорения, взяв производную вектора скорости по времени

,

,

где – проекции вектора ускорения на оси координат, а модуль полного ускорения определится как

.