2. Линейная интерполяция

Простейшим и часто используемым видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные точки (x_i, y_i) при (i = 0. 1, ..., n) соединяются прямолинейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках.

    Уравнения каждого отрезка ломаной в общем случае разные. Поскольку имеется n интервалов (x_i-_1,x_i), то для каждого из них в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки(x_i-1,y_i-1)  и (x_i,y_i), в виде

=

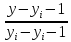    Отсюда

y=aix+bi , xi-1xxi

(*)

a_i=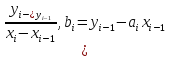

    Следовательно, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента х, а затем подставить его в формулу (*) и найти приближенное значение функции в этой точке

Рисунок 3-3- График зависимости линейной интерполяции [3].

2. Решение профессиональной задачи

Ведем экспериментальные данные

ORIGIN:=0 Начало массива данных - считаем с нуля

i:=1..6 Число элементов в массиве

Экспериментальные данные организованы в два вектора

Выполним интерполяцию встроенными функциями MathCad

Линейная интерполяция

Lf(x_i):=linterp(x,y,x)

Интерполяция кубическим спайном

CS:= cspline(x,y)

Строим кубический сплайн по экспериментальным данным

Lf(x_i):=linterp(x,y,x_i)

Интерполяция В- сплайном

Задаем порядок интерполяции. В векторе u должно быть на (n-1) меньше элементов, чем в векторе x, причем первый элемент должен быть меньше или равен первому элементу x, а последний - больше или равен последнему элементу x.

_n:=3

BS:=bspline(x,y,u,n)

Cтроим В- сплайн по экспериментальным данным

BSf(x_i):=(BS, x,y,x_i)

Строим график всех функций аппроксимации на одной координатной плоскости.

_i:=0..10

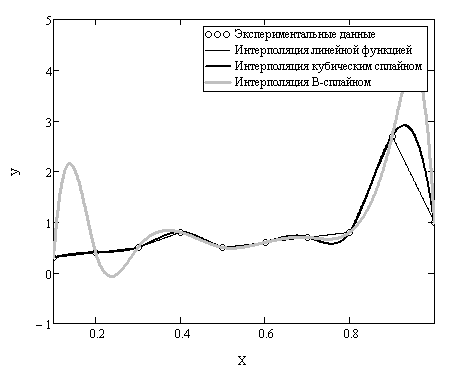
Рисунок 4.1-График всех функций аппроксимации на одной координатной плоскости.

Заключение

В вычислительной математике существенную роль играет интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение. На практике часто возникает задача о восстановлении непрерывной функции по ее табличным значениям, например, полученным в ходе некоторого эксперимента. Для вычисления многих функций, оказывается, эффективно приблизить их полиномами или дробно-рациональными функциями. Теория интерполирования используется при построении и исследовании квадратурных формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений. Основным недостатком полиномиальной интерполяции является то, что она неустойчива на одной из самых удобных и часто используемых сеток - сетке с равноудаленными узлами. Если позволяет задача, эту проблему можно решить за счет выбора сетки с Чебышевскими узлами. Если же мы не можем свободно выбирать узлы интерполяции или нам просто нужен алгоритм, не слишком требовательный к выбору узлов, то рациональная интерполяция может оказаться подходящей альтернативой полиномиальной интерполяции.

К достоинствам сплайн-интерполяции следует отнести высокую скорость обработки вычислительного алгоритма, поскольку сплайн - это кусочно-полиномиальная функция и при интерполяции одновременно обрабатываются данные по небольшому количеству точек измерений, принадлежащих к фрагменту, который рассматривается в данный момент. Интерполированная поверхность описывает пространственную изменчивость различного масштаба и в то же время является гладкой. Последнее обстоятельство делает возможным прямой анализ геометрии и топологии поверхности с использованием аналитических процедур