- •1.Частные производные, дифференциалы высших порядков функции нескольких переменных.
- •3. Дифференциал функции нескольких переменных.
- •4Дифференцирование сложных функций нескольких переменных.
- •5 Производная по направлению, градиент(grad)
- •6. Экстремум функции нескольких переменных (необходимое условие).
- •7. Условный экстремум функции нескольких переменных, функция Лагранжа.
- •8.Первообразная функция, Неопределенный интеграл и его св-ва.
- •15.Интегрирование иррациональных выражений
- •16.Определенный интеграл.
- •17. Св-ва опред.Интегралов.Интегральная теорема о среднем.
- •18.Формула Ньютона-Лейбница.
- •24,25, 26.Вычисление дуг линий.
- •27.Вычисление объемов тел вращения.
- •28. Несобственные интегралы первого рода.
- •31, 32 Двойные интегралы
- •33.Тройной интеграл . Вычисление тройного интеграла в дикартовых координатах.
- •34 Замена переменных в тройном интеграле.
- •35 Тройной интеграл цилиндрических поверхностях
- •36 Тройной интреграл в сферических координатах
- •37 Кри-1
- •38 Ориентированая кривая. Задачи привод к кри-2
- •39 С-ва кри-2. Вычисление кри-2. Связь между кри-1 и кри-2
- •40. Формула Грина
- •44 Ориентированная поверхность. Задачи приводящие к пи-2
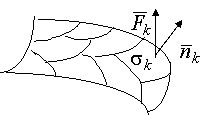
- •46 Векторное поле. Поток вектора через поверхность
- •47 Формула Остроградского-Гаусса
- •48 Дивергенция векторного поля
- •50. 52. Циркуляция векторного поля. Ротор(вихрь)
- •51 Формула Стокса
- •53 Потенциальное поле. Условие потенциальности, свойства.
- •53. Векторные диф операции 1 и 2 порядка. Оператор Гамильтона
40. Формула Грина
С помощью формулы Грина устанавливают связь между двойным интегралом по некоторой плоской области D и КРИ по границе Lэтой области
Пусть D плоской области ограничена линией L в замкнутой области D, заданы непрерыв фун X(xy) Y(xy) которые имеют непрерыв частные производные.
Пусть
граница М состоит из L1
и L2
заданы уравнением
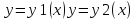 наL
задан направление движения чтобы этом
движ области D
… с левой стороны при обходе L
против часовой стрелки. Вычислим 2-ой
интеграл
наL
задан направление движения чтобы этом
движ области D
… с левой стороны при обходе L
против часовой стрелки. Вычислим 2-ой
интеграл

Вычислим КРИ по кривой L

Сравним правые части ур (1) и (2)

Аналогично доказ что справедливо след равенство
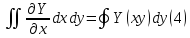
Сложим (3) и (4)

(5)- формула Грина
44 Ориентированная поверхность. Задачи приводящие к пи-2
Проведем в точку Р поверхностиQ нормаль, фиксир одну из возможных направл этих нормалей. Единичная величина направ по нормалям в установленом на ней направлении обзначается через n(P). Если это возможно сделать то поверхность Q вместе с направ нормалями устанавливает направление ее точки наз ориентир поверх
Задача
о вычислении потока жидкости через
поверхность.
Дана пространственная область, заполненная
жидкостью, движущейся со скоростью ![]() .
Требуется вычислить количество жидкости,
протекающей в единицу времени через
данную поверхность
.
Требуется вычислить количество жидкости,
протекающей в единицу времени через
данную поверхность![]() Разобьем
поверхность на
Разобьем
поверхность на![]() элементарных
частей, площади которых равны
элементарных
частей, площади которых равны![]() ,
а диаметры
,
а диаметры![]() .
Выберем в каждой некоторую точку
.
Выберем в каждой некоторую точку![]() и
будем считать, что скорость для всех
точек элементарной части одинакова и
равна
и
будем считать, что скорость для всех
точек элементарной части одинакова и
равна![]() .Количество
жидкости, протекающей через
.Количество
жидкости, протекающей через![]() за
единицу времени, равно произведению
за
единицу времени, равно произведению![]() ,
где
,
где![]() –
проекция скорости
–
проекция скорости![]() на
ось, определяемую единичным вектором
нормали
на
ось, определяемую единичным вектором
нормали![]() к
поверхности к точке
к
поверхности к точке![]() .
Тогда количество жидкости можно найти
по формуле
.
Тогда количество жидкости можно найти
по формуле![]() ,
где
,
где![]() –
углы, образованные нормалью
–
углы, образованные нормалью![]() с
координатными осями.
В результате
количество жидкости, протекающей через
всю поверхность за единицу времени,
приближенно выражается формулой
с
координатными осями.
В результате
количество жидкости, протекающей через
всю поверхность за единицу времени,
приближенно выражается формулой![]() .
Проекции
элементарной поверхности
.
Проекции
элементарной поверхности![]() на
координатные плоскости
на
координатные плоскости![]() выражаются
следующим образом
выражаются
следующим образом![]() ,
,![]() ,
,![]() .
Тогда
количество жидкости выражается следующим
образом
.
Тогда
количество жидкости выражается следующим
образом![]() .
Будем
увеличивать число разбиений так, чтобы
наибольший из диаметров областей
.
Будем
увеличивать число разбиений так, чтобы
наибольший из диаметров областей![]() стремился
к нулю.
Количество жидкости, проходящей
через поверхность в единицу времени
можно найти по формуле
стремился
к нулю.
Количество жидкости, проходящей
через поверхность в единицу времени
можно найти по формуле .
.
45
вычисление
поверхностного интеграла второго
рода
Пусть
поверхность ![]() определена
уравнением
определена
уравнением![]() ,
заданным в области
,
заданным в области![]() –
проекции поверхности
–
проекции поверхности![]() на
плоскость
на
плоскость![]() .
Тогда поверхностный интеграл второго
рода по переменным
.
Тогда поверхностный интеграл второго
рода по переменным![]() и
и![]() можно
свести к двойному интегралу.
можно
свести к двойному интегралу.![]() .
Знак
зависит от выбора стороны
поверхности
.
Знак
зависит от выбора стороны
поверхности![]() .
Аналогично
получаем:
.
Аналогично
получаем:![]() ,
,![]() .
В
общем случае получаем
.
В
общем случае получаем Можно
показать связь между поверхностными
интегралами первого и второго рода.
Можно
показать связь между поверхностными
интегралами первого и второго рода.![]()
46 Векторное поле. Поток вектора через поверхность

Изучение
поля скоростей текущей жидкости приводит
к понятию потока поля. Рассмотрим
простейший случай, когда скорости ![]() всех
частиц стационарно текущей жидкости
одинаковы.
всех
частиц стационарно текущей жидкости
одинаковы.
Возьмём
в этом потоке плоскую площадку ![]() .
.
Объём ![]() жидкости,
которая протекает в единицу времени
сквозь
жидкости,
которая протекает в единицу времени
сквозь![]() ,
будет равен объёму цилиндра с основанием
,
будет равен объёму цилиндра с основанием![]() и
образующей
и
образующей![]() :
:![]() ,
где
,
где![]() -
единичный вектор нормали к площадке
-
единичный вектор нормали к площадке![]() ,
т. е.
,
т. е.![]()
![]() .
Здесь
.
Здесь![]() .
Полученный объём
.
Полученный объём
Сделаем
обобщение этого элементарного понятия
на случай произвольного векторного
поля и произвольной поверхности ![]() .
.
Рассмотрим
некоторую поверхность ![]() в векторном поле
в векторном поле![]() .
На данной поверхности выделим некоторую
достаточно малую область
.
На данной поверхности выделим некоторую
достаточно малую область![]() (Рис.9).
В этой области возьмём точку
(Рис.9).
В этой области возьмём точку![]() ,
,![]() . К
поверхности
. К
поверхности![]() построим
касательную плоскость
построим
касательную плоскость![]() ,
касающуюся поверхности в точке
,
касающуюся поверхности в точке![]() .
.
На
касательной плоскости ![]() определим
плоскую площадку
определим
плоскую площадку![]() ,
равновеликую
,
равновеликую![]() .
Площадку
.
Площадку![]() примем
за основание цилиндра, образующие
которого равны по длине и параллельны
вектору поля
примем
за основание цилиндра, образующие
которого равны по длине и параллельны
вектору поля![]() в
точке
в
точке![]() .
.
Как
уже отмечено выше, объём полученного
цилиндра даёт элементарный поток через
область поверхности ![]()
|
|
|
|
| ||
|
|
|
| |||
|
|
|
| |||
|
|
|
| |||
Рис.
10. Разбиение области ![]() на
частичные области
на
частичные области
 (41)
(41)
Этот
предел поверхностной интегральной
суммы не зависит ни от способа дробления
области ![]() на
частичные области
на
частичные области![]()
![]() ,
ни от выбора точек
,
ни от выбора точек![]() на
каждой из них, и равен поверхностному
интегралу. Получаем основную формулу
потока поля
на
каждой из них, и равен поверхностному
интегралу. Получаем основную формулу
потока поля![]() через
поверхность
через
поверхность![]() в направлении
единичной нормали
в направлении
единичной нормали![]()
![]() . (42)
. (42)