33.Тройной интеграл . Вычисление тройного интеграла в дикартовых координатах.

Тройной интеграл также явл. Частным случаем определенного интеграла. Пусть имеет объем определенную замкнутую поверхность, разобъем эту поверхнусть на простр. Ячейки, объемом. Каждой ячейке.возьмем

;

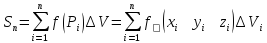(1)

v-область интегр;

x, y, z,-переменная интерп. Обл

dv-дифир. Объекта проним. Облv

Предположим что вычисление тройного интеграла сводится к к последов. Трех интегралов по каждой их перем x,y,z, от каждой фун.

Пусть v(тело) правит в направлении от осиOZпространственной области ограниченной замкнйтой поверхностью, это значит что переменная М от осиOZперенесеи границу области не более чем в двух точках воспоиз. Механ. Интерполир. Трехмерного интеграла как массы М телаvпри условии чтоf(x,y,z) плотностью распред. Массы

(2)

Вычисли массу фигуры другим способом. Предположим что тело vограничено поверхностями:

Возьмем электр площадку предположим область D,S=dsи вычислим массу вырезанного цилиндра поверхность причем образующей этой поверхности паралельнаOZа направляющейимеющую граниу электр.площади.

Вы делим на z, из стерии элемент длинойds,vэтого элементаds*dzа масса его приближ. Равнаf(x,y,z)ds,dz.

Для того чтобы найти массу рассматриваемой фигуры надо проинтегрировать массу всех таких элементов

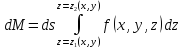
Чтобы получить массу всего тела vнадо просумировать массы частей этого тела

(3)

Сравним (2) и (3) и получим (4):

(4)

Если плоская область Dправильная например направлена оси

(5)

Из (5) следует что вычисление тройного интеграла в дикартовых координатах сводится к последовательному интегированию f(x,y,z) по всем переменным в рассматриваемом случае сначало вычисляем внутренний интегал по переменнойzпотом средний по переменнойyа внешний по переменнойx. Пределы во внешнем и среднем интеграле расставляются по плоской областиDкоторая явл проекцией пространственной областиVна координатной плоскости. Для того чтобы найти приделы интегрировалия во внутреннем интеграле достоточно через любую точку областиDпровести перпендикулярную к ней прямую и найти ее точки пересечения с поверхность ограниченой областиV.

Замечание.Если Vне удовлетворяет указонному выше условию то ее разбивают на сумму областей и тогда интегр будет равно сумме интегр по сост области.

Фигуру Vможно проинтегрировать не только на плоскостиOXYно и на любую другую координатную плоскость соблюдении условия тогда в трехгранном интеграле будет меняться порядок интегрирования.

34 Замена переменных в тройном интеграле.

Пусть в 3-ом интеграле необходимо заменить (x,y,z) на новые переменные (ūv)

(1)

Пусть непрерывны вместе со своими частными производными в некоторой области К и взаимно что отображает область К в дикартовой координат(xy,z)на область К’ приним коордэти значения имеют не только в каждой точкеP’(u v ω) из областиK’ соответ единственная точка Р(x,y,z) из области К и наоборот.

Элемент объема dvобласти К переходит в элемен объемdv’K’

Dv= dv’

J=

Dv’=dudvd

Тогда в тройном интеграле …фотрмула для замены интегралов

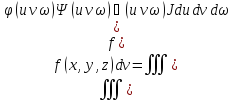(2)