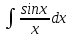7. Условный экстремум функции нескольких переменных, функция Лагранжа.

Если необходимо найти минимум или максимум функции 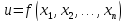, на переменные которых налагаются дополнительные ограничения:–уравн. связи. То говорят, что решают задачу нахождения условного экстремума.

Решим задачу нахождения условного экстремума для функции ; переменные которого связаны уравнением связи:.Функцией Лагранжа для этой задачи будем называть функцию:

Условный экстремум для функции при выполнении условий связибудет тогда, когда существуют числачто точкабудет точкой локального экстремума для функции ЛагранжаВерно и наоборот.

8.Первообразная функция, Неопределенный интеграл и его св-ва.

Функция y=F(x) наз.первообразной для функции y=f(x) на промежутке,еслиF’(x)=f(x) для любого х

Теорема:функция y=F1(x),y=F2(x)будут первообразными для функции y=f(x) на промежутке тогда и только тогда,когдаF1(x)-F2(x)=C(с доказат.)

Неопределенным интегралом для функции f(x) будем наз.совокупность всех первообразных для данной функции и будем обозначать =F(x)+C

Св-ва неопред. интегралов:

1.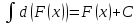-др.вид формулы

2.d(

3. (есть доказ.)

4.(есть доказ.)

5.,

10.Интегрирование по частям в неопред.интеграле.

Пусть u(x),v(x)-непрерывно диффер.и существует интеграл ,тогда существует интеграл

Замечание: это многочленn-ой степени

1)

U

dv

2)*

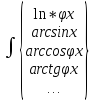U dv

11.Замена переменных в неопред.интеграле

Пусть функция y=f(x) интегрируема на промежутке ,а функцияx=-непрерывна дифференцируема на промежутке, тогдаf(-интегрир.на промеж.и

или

или

.

Формула(3)наз.-формулой интегрирования с помощью поднесения под дифференц.

!

При поднесении под диффер.можно использовать равенства:

dx=d(x+C) и dx=1/C*d(Cx)

Иногда правая часть в формуле (3)вычисл.сложнее чем левая,тогда ее переписывают в виде:=

12 Интегрирование элементарных рациональных дробей.

Функция R(x)=/(частное двух многочленов),наз.рацион.функцией,при этом еслиn<m,дробь наз.правильной,если n>=m,дробь наз.неправильной,а функции ; ;;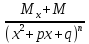- наз.элементарными рациональными дробями.

Проинтегрируем элемент.дроби:

1)

2)

3) (

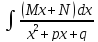4))

Перв. интеграл вычисл. поднесением под диффер.,во втором интеграле получают регурентное соот. выраж. интеграл n-ой степени от интеграла n-1 степени.

13.Интегрирование рациональных функций.

Функция вида R(u1,u2,...,)=, где P и Q-рациональные функции(многочлены переменных ) называется рациональной

Пункт1. Интегралы вида , ,...,)dx сделаем подстановку,где s-общий знаменатель дробей ,,

Найдем x и dx

ax+b=

x(a-c)=d-b

x=

dx=

После подстановки в интеграл все корни пропадают

14.Интегрирование тригонометрических выражений.

Пункт1.

Интегралы вида -рацион.функция.В этом случае подставляемtg-универсальная тригон.подстановка.

вида -универс.тригон.подстановка.

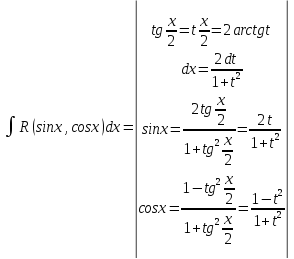
Пункт2.

Интегр. вида ,гдеm,n-целые числа и хотя бы одно из них нечетное.В этом случае берут сомножитель в первой степени от неч.степени и подносят его под диффер.

Пункт3.

Интегр.вида ,m,n-положительные и обе степени четные. В этом случае понижают степень.

Пункт4.

Интегр.вида ,m,n,m+n=-2k-четное отрицательное.В этом случае делаю замену tgx=t

Пункт5.

Интегр.вида ,tgx=t ctgx=t

Замечание: если y=f(x)-непрерывна,то первообразная для нее всегда сущ. ,но не для всякой непрерывной функции.Эту первообразную можно выразить через элементарные функции,,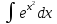