35 Тройной интеграл цилиндрических поверхностях

В этой системе координат положим что Р в пространстве определяется з-ым числом ( r 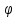z) гдеrинекоторые координаты т очки Р плоскостиOXYz-апликата точки Р

Координаты ( r φ z) цилиндрические в случае переходп у цилиндричским координатам (2)( u=rv= φ ω=z)

Между дикартовыми и цилиндрическими координатами существует зависимость

(3)

Найдем определитьель Якобы

==

J=r

Поэтому (2) при переходе от дикартовых координат к цилиндрическим имеет следующий вид

r φ z)(4)

36 Тройной интреграл в сферических координатах

Р(

Положим что Р определяется 3-мя координатами r φ θ, где r- расстояние до Р от начала координат так наз радиус вектора точки. Φ- угол между проекцией радиус вектора на плоскость OXYи осOX. Θ-это угол между вектором и осьюOZ.

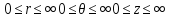
Связь между дикартовыми и сферическимии координатами задаются форумулой

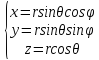(1)

(2)

Формула перехода к сферическим координатам

37 Кри-1

Пусть фигура Ф- плоская мн пространственная истин L

Мерой ее длинаlобозначая меруэлемент фигуры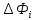черези пусть𝜆- наибольший из диаметров элемент фигуры, тогдаS_n имеет вид

Если предел этой суммы сущ то его наз КРИ- по длине дуги или КРИ-1

(1)

L-линия интегрирования

Вычисление КРИ-1

Рассмотрим кривую плоскость L

1. L

dx

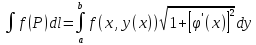(2)

Б)

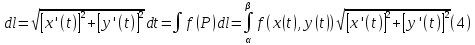
В)

38 Ориентированая кривая. Задачи привод к кри-2

Пусть в пространстве на плоскости задана кривая L. Кривую задан на ней двигают от А к В наз ориентированой кривой. Если задать по L движение в обратную сторону то получим другую ориентированую кривую. Сост из кривой и направл движение по этой кривой…

Пусть точка Р(x y z) движется вдоль непрерывной линии L от точка А к точке В, под действием силы F которая меняется по величине и направлению при этом движется.

Запишем ее в следующем виде

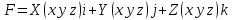
Вычислим работу А силы F при перемещении точки Р из A в B. Для этого разобьем крив АВ точками Р1, Р2, Рn-1 на n произвольных частей Δl1,Δl2,Δln в направлении от Ак Ви обозначим через ΔSi=Pi,Pi+1 Pi(xi yi zi) Pi+1(xi+1 yi+1 zi+1)

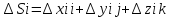
Вектор силы F точки Pi обозним через Fi=F(Pi) тогда приближ выражение для работы ΔAi силы А вдоль дуги Pi Pi+1 будет равно

Приближенное значение работы А силы F на кривой L будет равно

Правая часть (3) это интегр сумма для вектор фун Fi=F(Pi)

Если сущ предел выраж (3)( независящий от способа составления интегральной суммы)при 𝜆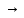0 то этот предел выражает работу А силыF то ариентир кривая L от А к В

Этот предел наз КРИ-2

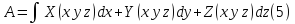
Данный интеграл наз КРИ по координатам в отличии от КРИ по длине дуги

, если L- замкнутая то иногда КРИ-2 обозначается? Указ неправ обхода по замкнутой кривойL

39 С-ва кри-2. Вычисление кри-2. Связь между кри-1 и кри-2

1)КРИ-2 зависит от подынтегрального выражения формы крив интеграла L от направ интеграла при изменении направления интеграла КРИ-2 меняется знак.

2) если кривая L разбита С на части

Вычисление КРИ-2 сводится к вычислению обычного определенного интеграла

Пусть кривая L задана параметрическим уравнением

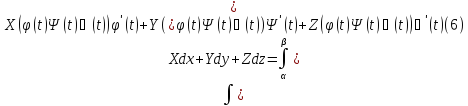
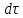Пусть на кривой L установлена напраление движения. Возьмем на этой кривой точку Р проведем к ней касательные кстанов на некотором направлении соответс направление движения по кривой. Отложим части в установленном направлении диф дуги dl. . Получимпроизвод которого служит дифdx, dy, dz, x, y, z- длина сооветсвенно

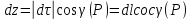
(2)-устанавливает связь между КРИ-1 и КРИ-2 рода