24,25, 26.Вычисление дуг линий.

Кривой линией l-наз.непрерывное отображение отрезка трехмерного пространства.Кривая наз.плоской если она целиком лежит в какой-то плоскости.

Замечание: Кривую L можно задавать в виде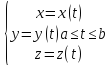-параметрическое задание кривой.На плоскости бывает задана в таком видеили в явном видеy=f(x) a.

Предположим,что функция y=f(x)непрер.дифференц.Разобьем отрезок [a,b] на n частичных отрезков и рассм.точки на кривой с координатами.

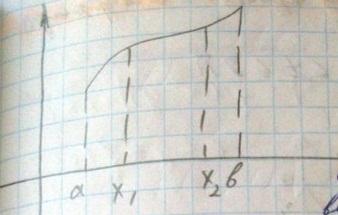
Рассмотрим ломаную соверш.в этих точках,тогда длина кривой

L=

Если функция задана параметр.

,то ее длина L=

А для кривой в полярных координатах r=r(

L=

27.Вычисление объемов тел вращения.

Рассмотрим пространсвенное тело.

Пусть проекция V=[a,b] и предположим,что для любого х из [a,b] известна площадь сечения S тела плоскостью х=х.Разобъем отрезок [a,b] на n частичных отрезков

Тогда объем тела V равен:

(1)

В частности если y=f(x)-непрерывна и f(x)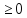рассм.фигуру фи Ф={(x,y) ,}

Будем вращать фигуру фи вокруг оси Ох,тогда из формулы 1следует,что

А при вращении этой же фигуры вокруг оси Оу

Рассмотрим фигуру Ф={(x,y) ,тогда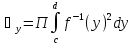

28. Несобственные интегралы первого рода.

Пусть функция y=f(x) определена на проме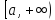жуткеи интегрируема на любом конечном промежутке: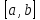

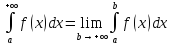
--несобственные интегралы первого рода

Если пределы в правых частях формул конечные, говорят, что интеграл сходится, в противном случае—расходится.

Признак сравнения: пусть. Тогда если интегралрасходится (сходится), то и интеграл–расходится (сходится).

Предельный признак сравнения: пусть,. Тогда интегралыисходятся или расходятся одновременно.

Пусть сходится, тогда говорят, что интеграл--сходится абсолютно. Если же-- расходится, а-- сходится, то говорят, что онсходится условно.

Несобственные интегралы второго рода.

Пусть функция y=f(x) определена на, интегрируема на любом отрезке;Тогданесобственным интегралом 2-го родабудет:

Аналогично: 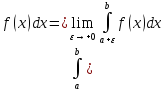для

Если то

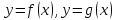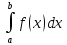Признак сравнения: пустьопределены на промежутке(в точке с разрыв 2-го рода), и. Тогда из сходимостиследует сходимость. А из расходимостиследует расходимость

Пусть определены и неотрицательны на множествеи пусть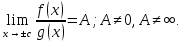Тогда интегралысходятся или расходятся одновременно.

31, 32 Двойные интегралы

Пусть Д – плоская область и S(Д) – площадь области Д. Диаметр областиd(Д)-максимальное расстояние между точками, принадлежащими этой области.

Пусть z=f(x,y) – функция, определенная на области Д со значениями во множестве действительных чиселR. Разобьем область Д наnчастных областей Д=таким образом, чтобы

S(Д) =

Пусть M(x,y) произвольная точка в области. Тогда число_n(f)=– называетсяn-ой интегральной суммой Римана.Если существуетнезависящий от способа разбиения области и выбора точекn,i, то он называется двойным интегралом по области Д по функцииf.

Свойства двойного интеграла

1. Пусть z=f(x,y)=1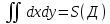- площадь области

2. Пусть в каждой точке области задана ее плотность (х,у). Тогда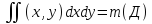-масса пластинки

3. Пусть z=f(x,y) непрерывна на области Д, а область Дзамкнута и ограничена. Тогда существует.

Вычисления двойных интегралов

Область Д называется правильной в направлении оси ОУ, если любая прямая, параллельная этой оси, пересекает границу этой области не более чем в двух точках. Аналогично определяется область, правильная в направлении оси ОХ.

Пусть область Д правильная в направлении оси ОУ. у=у₁(х) и у=у₂(х) – линии входа и выхода. Тогда

Аналогично ля области, правильной в направлении оси ОХ.