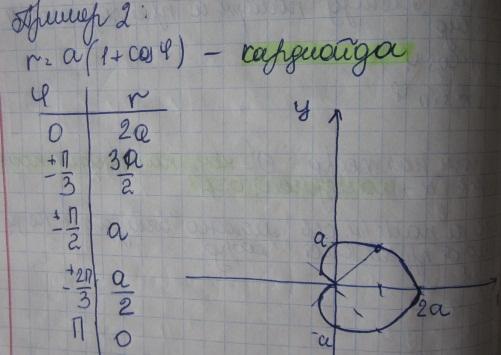15.Интегрирование иррациональных выражений

Пункт2. Интегралы вида

Интегралы вычисляются выделением полного квадрата,интегралы-в числителе выделяют производную квадратного трехчлена и сводят к вычислению интегралов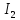

Пункт3. После выделения полного квадрата и замены, интеграл сведется к одному из следующих видов. Затем делаем такую тригонометрическую подстановку, чтобы корни пропали.

)dt=

16.Определенный интеграл.

Пусть функция y=f(x)-определена на (промежутке)отрезке [a,b].Разобьем его на n-частичных отрезков.

Пусть -длинаk-ого частичного отрезка,а -диаметр разбиения.

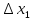Пусть наk-ом част.отрезке.Тогда сумма (f)=f()+f()+…+f(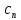)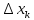(1)-наз. n-ой интегральной суммой Римана.

Если сущ.предел при → 0 интегральной суммы(1),независ. От способа разбиения отрезка и выбора точек,то отназ.определенным интегралом. (2)

Теорема:(теорема сущ.опред.интегралов) Если функция y=f(x) непрерывна,то опред.интеграл существует.

Пусть y=f(x)-непрерывн.функция ≥0 для любого x из[a,b],тогда фигура равна:a≤x≤b; 0≤y≤f(x)}-наз. криволинейной трапецией.

Замечание: =

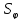a b

17. Св-ва опред.Интегралов.Интегральная теорема о среднем.

1) =b-a

2)f(x)≥0 и непрерывна

3)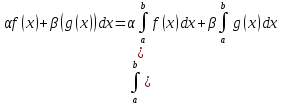(с доказат.)

4) Пусть y=f(x) интегрируема на отрезке [a,b],C[a,b],тогда

5) y=f(x)≥0,тогда

6) f(x)≥g(x) x[a,b],тогда 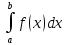≥f(x)≥g(x) f(x)-g(x)≥0

7) y=f(x)-непрерывна на [a,b],тогда она достиг. на этом отрезке свою точную нижнюю m и точн.верх.грань M

m(b-a)≤(с доказат.)

8)Пусть y=f(x) непрер.и на отрезке [a,b],тогда сущ.такая т.С из [a,b],что -интегральная теорема о среднем.(с доказат.)

Интегральная теорема о среднем.

Пусть y=f(x) непрер.и на отрезке [a,b],тогда сущ.такая т.С из [a,b],что 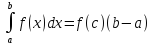-интегральная теорема о среднем.

Доказательство:m

Функция f(x) промеж.число между наиб. и наим.значен.,т.к функция непрер.,тообяз.найд.промеж.знач.С,что

18.Формула Ньютона-Лейбница.

Пусть y=f(x)-непрер.на [a,b]и-первообр.для функцииf(x),тогда

Доказательство: ,т.к любые две первообр.отлич.на константу,то,дляx ,еслиx=a

0=

C=-

,для 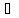x из [a,b];

в частности при x=b

19.Интегралы с переменным верхним пределом(непрерывность).Интегралы с переменным верхним пределом(дифференцируемость).

Теорема 1:пусть y=f(x)-интегрир.на [a,b]

Рассм.F(x)=

Тогда функция y=F(x)-непрерывна и y=G(x)=непрер.

Д-во:

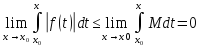
Если функция интегр.,то она ограничена сверху числом M.

Теорема: Пусть y=f(x)-непрер. На [a,b],тогда F(x)=-дифференцируема и ее производнаяF’(x)=f(x).Аналогично для функции G(x)=

G’(x)=-f(x)

До-во:

F’(x)==

Замечание: из теоремы следует,что функция F(x) явл. первообразной для функции y=f(x)

20.Замена переменных в определенном интеграле.

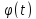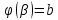
у=f(x)-непрер.на [a,b],а x=-непрерывна диффер.на [,причем=[a,b],тогда -замена переменной в опред.интеграле.

Доказательсвто:

Пусть y=F(x)-первообр.для функции f(x)

Рассм.функцию y=F(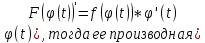

(

a

b

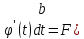*)-F(a)

21.интегрирование по частям в определенном интеграле.

Пусть u,v-непрер.диффер.функции,тогда --формула интегр.по частям

a

b

Доказательство:

d(uv)=udv+vdu

b

udv=d(uv)-vdu -

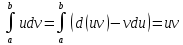a

22.Вычисление площадей в прямоуг.системе координат.

Пусть y=f(x)-нерпер.функция f(x)≥0 x

a≤x≤b,o≤y≤f(x)} ,тогда

b

a

x

Пусть y=f(x) и y=g(x)-непрер. f(x)≥g(x) x

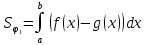
a

x

b

23.Вычисление площадей в полярной системе координат.

Пусть (O,i,j)прямоугольнач система координат на плоскости;М(произвольная точка плоскости).Полярными координатами точки М будем наз.длину ее радиус-вектора R и угол,образует радиус-вектор в положит.направлении оси Ox.При этом нач.координат О-наз.полярным полюсом, а полуось Ох-полярная ось.

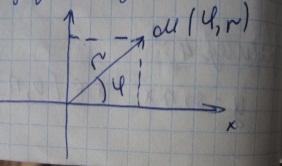
Пусть r=r()-уравнение кривой в полярн.системе координат.Рассмотрим фигуру Ф.

Ф={(. Разобъем Ф наn частичных фигур лучами

=

(
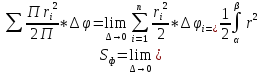