
- •1.Частные производные, дифференциалы высших порядков функции нескольких переменных.
- •3. Дифференциал функции нескольких переменных.
- •4Дифференцирование сложных функций нескольких переменных.
- •5 Производная по направлению, градиент(grad)
- •6. Экстремум функции нескольких переменных (необходимое условие).
- •7. Условный экстремум функции нескольких переменных, функция Лагранжа.
- •8.Первообразная функция, Неопределенный интеграл и его св-ва.
- •15.Интегрирование иррациональных выражений
- •16.Определенный интеграл.
- •17. Св-ва опред.Интегралов.Интегральная теорема о среднем.
- •18.Формула Ньютона-Лейбница.
- •24,25, 26.Вычисление дуг линий.
- •27.Вычисление объемов тел вращения.
- •28. Несобственные интегралы первого рода.
- •31, 32 Двойные интегралы
- •33.Тройной интеграл . Вычисление тройного интеграла в дикартовых координатах.
- •34 Замена переменных в тройном интеграле.
- •35 Тройной интеграл цилиндрических поверхностях
- •36 Тройной интреграл в сферических координатах
- •37 Кри-1
- •38 Ориентированая кривая. Задачи привод к кри-2
- •39 С-ва кри-2. Вычисление кри-2. Связь между кри-1 и кри-2
- •40. Формула Грина
- •44 Ориентированная поверхность. Задачи приводящие к пи-2
- •46 Векторное поле. Поток вектора через поверхность
- •47 Формула Остроградского-Гаусса
- •48 Дивергенция векторного поля
- •50. 52. Циркуляция векторного поля. Ротор(вихрь)
- •51 Формула Стокса
- •53 Потенциальное поле. Условие потенциальности, свойства.
- •53. Векторные диф операции 1 и 2 порядка. Оператор Гамильтона
1.Частные производные, дифференциалы высших порядков функции нескольких переменных.
Пусть
функция
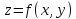 --
дифференц.,
--
дифференц.,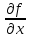 и
и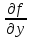 –ее частные производные (функции от х
и у). Производная от частных производных
функции
–ее частные производные (функции от х
и у). Производная от частных производных
функции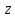 (если они существуют)—вторые
производные
функции
(если они существуют)—вторые
производные
функции
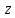 .
Таким образом:
.
Таким образом: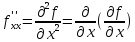 ;
;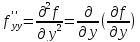 ;
;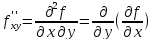 --смешанная
производная.
--смешанная
производная.
Пусть
в некоторой окрестности
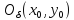 существует частная производная:
существует частная производная: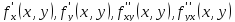 для функции
для функции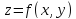 .
И пусть произв.
.
И пусть произв.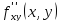 и
и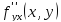 непрерывны в точке
непрерывны в точке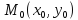 .
Тогда они равны.
.
Тогда они равны.
Пусть
функция
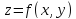 —дифференц.
и
—дифференц.
и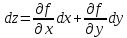 —ее
дифференциал, функция 4-ех переменных.
Зафиксир.
—ее
дифференциал, функция 4-ех переменных.
Зафиксир. и
и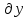 ирассмотрим дифференциал от дифференциала.
Дифференциал от первого дифференциала
от функции
ирассмотрим дифференциал от дифференциала.
Дифференциал от первого дифференциала
от функции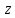 (если он существует) назыв. вторым
дифференциалом:
(если он существует) назыв. вторым
дифференциалом: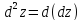 .
Аналогично:
.
Аналогично: –
–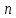 -ый
дифференциал функции.
-ый
дифференциал функции.
Пусть
функция
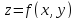
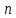 раз дифференц. в некоторой окрестности
в точке
раз дифференц. в некоторой окрестности
в точке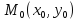 .
Тогда она представляется в этой
окрестности в виде:
.
Тогда она представляется в этой
окрестности в виде: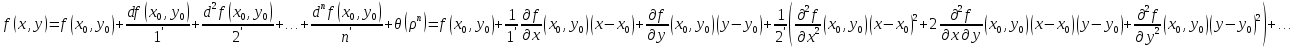 --формула
Тейлора,
где
--формула
Тейлора,
где
 .
.
 +
+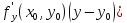 –приближенное
вычисление.
–приближенное
вычисление.
3. Дифференциал функции нескольких переменных.
Пусть
функция
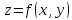 дифференц.
в точке
дифференц.
в точке
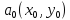 .
Линейная, относительно
.
Линейная, относительно ,
функция
,
функция
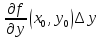 назыв.
дифференциалом.
назыв.
дифференциалом.
Для
функции
 :
: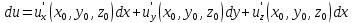
4Дифференцирование сложных функций нескольких переменных.
Пусть
функция
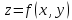 дифференц.
в точке
дифференц.
в точке
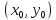 ,
а функции
,
а функции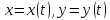 в
точке
в
точке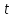 .
Причем
.
Причем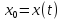 .
Тогда сложная функция
.
Тогда сложная функция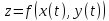 дифференц. в точке
дифференц. в точке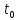 .
И ее производная:
.
И ее производная: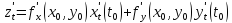 .
.
Пусть
функция
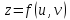 дифференц.
в любой точке (u,v)
и функции
дифференц.
в любой точке (u,v)
и функции
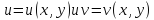 дифференц. в любой точке
дифференц. в любой точке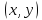 .
Тогда сложная функция
.
Тогда сложная функция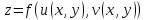 --также
дифференц., причем ее частная производная
:
--также
дифференц., причем ее частная производная
: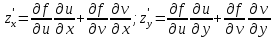
Дифференцирование неявных функций нескольких переменных.
Пусть
функция
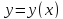 задана неявно в виде
задана неявно в виде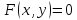 .
Т.е.
.
Т.е.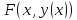 для
для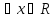 ,
, --дифференц.
Возьмем производную от обеих частей:
--дифференц.
Возьмем производную от обеих частей: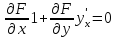 ;
;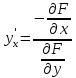
Пусть
функция
 задана неявно в виде
задана неявно в виде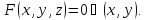 Возьмем производную от обеих частей
этого равенства:
Возьмем производную от обеих частей
этого равенства: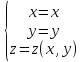 ;
;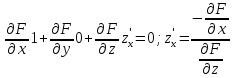 ;
;
Возьмем
производную от обеих частей этого
равенства по y:

5 Производная по направлению, градиент(grad)
Функция
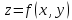 определена
в некот. окрестности точки
определена
в некот. окрестности точки
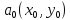 ,
,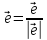 --вектор единичной длины сонаправл. с
--вектор единичной длины сонаправл. с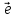 .
Производная по направлению с
.
Производная по направлению с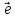 :
: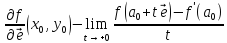 .
.
Пусть
 --направл. косинусы вектора
--направл. косинусы вектора .
Тогда
.
Тогда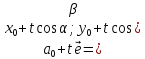 :
:
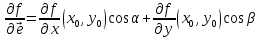 —формула
производной по направлению.
—формула
производной по направлению.
Градиентом
для
функции
 в точке
в точке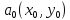 будем называть вектор
будем называть вектор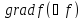 ,
координаты которого:
,
координаты которого: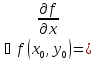
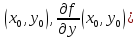 .
=>
.
=>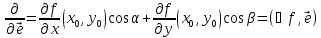
 .
Наименьшее значение производной при
.
Наименьшее значение производной при
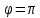 ,
тогда
,
тогда противопол. направлению
противопол. направлению .
Наибольшее значение производной
получается при
.
Наибольшее значение производной
получается при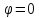 ,
т.е. направление
,
т.е. направление совпадает с направлением
совпадает с направлением .
. задает направление наиб. возраст.
Функции, а модуль градиента—скорость
наиб. возрастания функции.
задает направление наиб. возраст.
Функции, а модуль градиента—скорость
наиб. возрастания функции.
Касательная плоскость.
Пусть
 дифференц. в точке
дифференц. в точке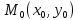 .
Тогда плоскость
.
Тогда плоскость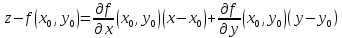 --касательная
плоскость к поверхности
--касательная
плоскость к поверхности
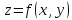 в точке
в точке
Если
поверхность задана неявно в виде
 токасательная
плоскость
к данной поверхности в точке
токасательная
плоскость
к данной поверхности в точке
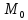 записывается в виде:
записывается в виде: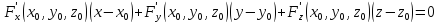
Нормаль к поверхности.
Нормаль
к поверхности
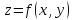 в
точке
в
точке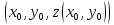 :
: .
.
Если
поверхность задана неявно в виде
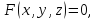 тонормаль
записывается
в виде:
тонормаль
записывается
в виде:
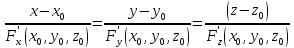
6. Экстремум функции нескольких переменных (необходимое условие).
Пусть
функция
 определена в некоторой окрестности
определена в некоторой окрестности в точке
в точке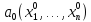 .
Точка
.
Точка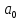 --локальный
максимум (локальный минимум),
если выполняется:
--локальный
максимум (локальный минимум),
если выполняется:
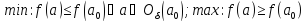
Необходимое
условие экстремума: пусть
точка
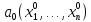 является локальным экстремумом для
функции
является локальным экстремумом для
функции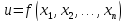 .
Тогда частные производные в этой точке
равны 0 или не существуют. Точки, в которых
частная производная функции равна 0 или
на существует, называютсякритическими
точками.
Любая точка локального экстремума
является критической, а наоборот не
верно.
.
Тогда частные производные в этой точке
равны 0 или не существуют. Точки, в которых
частная производная функции равна 0 или
на существует, называютсякритическими
точками.
Любая точка локального экстремума
является критической, а наоборот не
верно.
Экстремум функции нескольких переменных (достаточное условие).
Пусть
функция
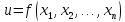 определена в некоторой окрестности
определена в некоторой окрестности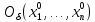 в точке
в точке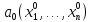 .
Точка
.
Точка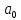 --локальный
максимум (локальный минимум),
если выполняется:
--локальный
максимум (локальный минимум),
если выполняется:
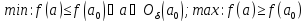
Достаточное
условие экстремума: пусть
функция
 дважды
дифференцирована в окрестности
дважды
дифференцирована в окрестности
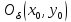 в своей критической точке
в своей критической точке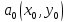 (частные производные первого порядка
=0 в этой точке). Пусть
(частные производные первого порядка
=0 в этой точке). Пусть .
Рассмотрим определитель:
.
Рассмотрим определитель: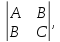 тогда:
тогда:
если
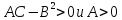 ,
то точка
,
то точка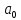 является точкойлокального
минимума;
является точкойлокального
минимума;
если
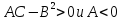 ,
то
,
то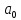 --локальный
максимум;
--локальный
максимум;
если
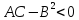 —локального
экстремума в
—локального
экстремума в
 нет.
нет.
