Davis W.A.Radio frequency circuit design.2001

80 MULTIPORT CIRCUIT PARAMETERS AND TRANSMISSION LINES

The sum of the rows can also be shown to be 0. If the same voltage v0 is added to each of the terminal voltages, the terminal currents would remain unchanged:

So that the sum of the rows is 0. A variety of other important properties of the indefinite admittance matrix are described in [1, ch. 2] to which reference should be made for further details.

One of the useful properties of this concept is illustrated by the problem of converting common source hybrid parameters of a FET to common gate hybrid parameters. This might be useful in designing a common gate oscillator with a transistor characterized as a common source device. The first step in the process is to convert the hybrid parameters to the equivalent definite admittance matrix (which contains two rows and two columns) by using the formulas in Appendix E. The definite admittance matrix, which has a defined ground, can be changed to the corresponding 3 ð 3 indefinite admittance matrix by adding a column and a row such that rows D 0 and the columns D 0. If the y11 corresponds to the gate and y22 corresponds to the drain, then y33 would correspond to the source:

g d s

gy11 y12 y13

The common gate parameters are found by forcing the gate voltage to be 0. Consequently the second column may be removed, since it is multiplied by the zero gate voltage anyway. At this point the second row represents a redundant equation and can be removed. In this case row 2 and column 2 are deleted, and a new common gate definite admittance matrix is formed. This matrix can then be converted to the equivalent common gate hybrid matrix.

4.10THE INDEFINITE SCATTERING MATRIX

A similar property can be determined for the scattering matrix. The indefinite scattering matrix has the property that the sum of the rows D 1 and the sum

Radio Frequency Circuit Design. W. Alan Davis, Krishna Agarwal

Copyright 2001 John Wiley & Sons, Inc.

Print ISBN 0-471-35052-4 Electronic ISBN 0-471-20068-9

CHAPTER FIVE

Filter Design and

Approximation

5.1INTRODUCTION

The subject of network synthesis became highly refined in the twentieth century due to the work of some very capable electrical engineers. To work through that body of knowledge would be beyond the present purpose of reviewing filter synthesis techniques. This chapter will therefore concentrate on basic techniques and solutions to the filter approximation problem and implementations that have come about by special requirements. At this point in time, operational amplifiers have not made a significant inroad to the RF frequency range, so active filters will not be treated here. However, active filter design is discussed by Chen [1]. Filters and impedance matching circuits are vital in the design of transistor amplifiers. The particular values of impedances needed for an amplifier depend on the device type and its orientation. Formulas for these impedances are summarized in Appendix D.

The solutions to the filter approximation problem and implementations that have arisen because of special requirements are treated in this chapter. The treatment is further limited to filters that perform certain tasks on continuous time varying analog signals by way of linear time-invariant circuit elements. Such filters are called analog filters. These analog filter functions are frequency selective circuits, and they can be analyzed in the time domain or in the frequency domain using Fourier transforms and Laplace transforms.

5.2IDEAL AND APPROXIMATE FILTER TYPES

The function of a filter is to separate different frequency components of the input signal that passes through the filter network. The characteristics of the network are specified by a transfer function, H jω or H s , where s D Cjω represents

84

the complex frequency defined for the Laplace transform. The transfer function is the ratio of output signal to input signal, voltage, or current:

The transfer phase function, ω , is related to the transfer group delay through a differential with respect to frequency as follows:

For constant group delay, the phase function must be linear with frequency. In most filters only the magnitude of the transfer function is of interest. However, in modern-day systems using signals with complex modulation schemes, phase and group delay functions are also important.

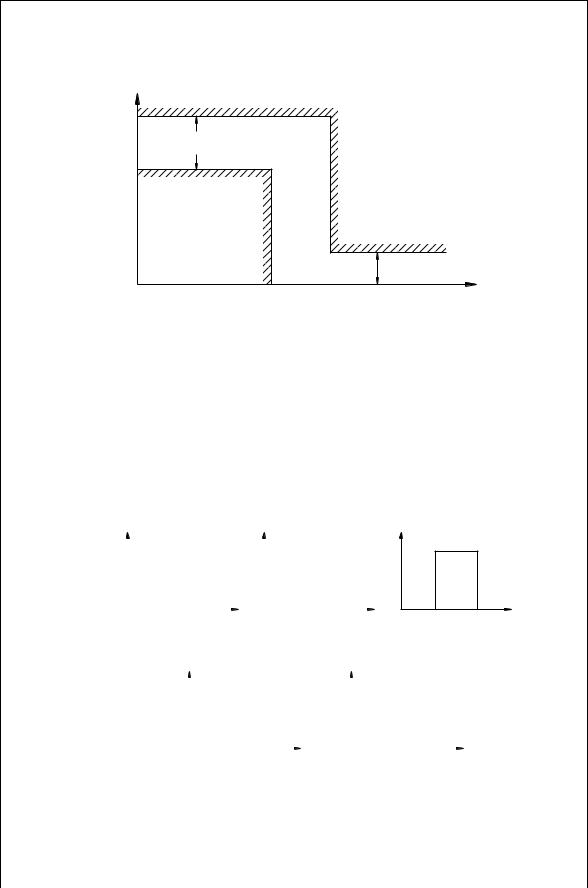
A filter network passes some of the input signal frequencies and stops others, and being a linear circuit, this function is performed without adding or generating new frequency components. The frequency band that passes, ideally without losses (0 dB insertion loss), defines the pass band, and the band that stops the frequencies, ideally with infinite loss, is called the stop band. Figure 5.1 shows this loss representation of the ideal low-pass filter. It is a low pass because it passes all low-frequency signals from dc to some high frequency, ωc and stops all signals above ωc. The frequency, ωc, is called the cutoff frequency of the filter. An ideal low-pass filter is physically not realizable as this requires a circuit with an infinite number of elements due to an abrupt change from pass band to stop band. Such a change is not practical.

This raises a practical issue of how does one specify the filters? The concept of the transition band, ωp to ωs, is the frequency range that separates the pass band and stop band where the loss transitions from a minimum to a maximum value. This is shown in Fig. 5.2. The ratio of ωs/ωp is sometimes referred to as filter selectivity, ratio, or filter steepness. As the selectivity approaches one,

FIGURE 5.1 Loss or attenuation characteristics of an ideal low-pass filter.

86 FILTER DESIGN AND APPROXIMATION

FIGURE 5.2 Method of specifying a practical low-pass filter.

the more complex and costly the filter becomes. Similar considerations can be applied in the design of filters using phase linearity and/or group delay flatness. The concept of pass band, stop band, and transition band permits specifications of five major types of filters: (1) low pass, (2) high pass, (3) band pass, (4) band stop, and (5) all pass. The transmission behavior of these filters is shown in Fig. 5.3.

FIGURE 5.3 The five major filter types using transfer function amplitude response.

5.4LADDER NETWORK FILTERS

The class of minimum phase filters are those filters in which the zeros of the impedance function are chosen to be in the left half-plane. This is a way of saying that the topology of a low-pass filter is a ladder network. The filter is assumed to be lossless and terminated on each side by a real resistance. As indicated in Fig. 5.4, there are four possible choices for the first and last reactive elements. The final reactive element depends on whether the number of elements is even or odd. The basic procedure is to develop a design for a low-pass filter whose terminating resistors are 1 and whose cutoff frequency is ωc D 1 rad/s. Once this normalized low-pass filter is designed, the impedance level is adjusted to the desired value, the cutoff frequency is adjusted, and circuit topology is transformed to a high-pass, band-pass, or band-stop filter as desired.

The notation for the low-pass filter prototype filter with g values, shown in Fig. 5.4, is widely used. In this way convenient recursion formulas can be used for finding the filter values. A g beside an inductor stands for inductance, a g beside a capacitor stands for capacitance, and a g beside a resistor stands for resistance. For the normalized prototype circuit, g0 D 1.

5.4.1The Butterworth Filter

The transducer power gain for a two port circuit is

which for a passive filter is a quantity 1. A filter with many reactive elements would be expected to more closely approximate an ideal filter with rectangular shape (infinitely steep band edge skirts and flat-pass band) than one with few reactive elements. For a filter with n poles (n reactive elements), the low-pass Butterworth approximation provides the maximum flatness in its pass band near

FIGURE 5.4 The lumped element prototype low-pass filter.